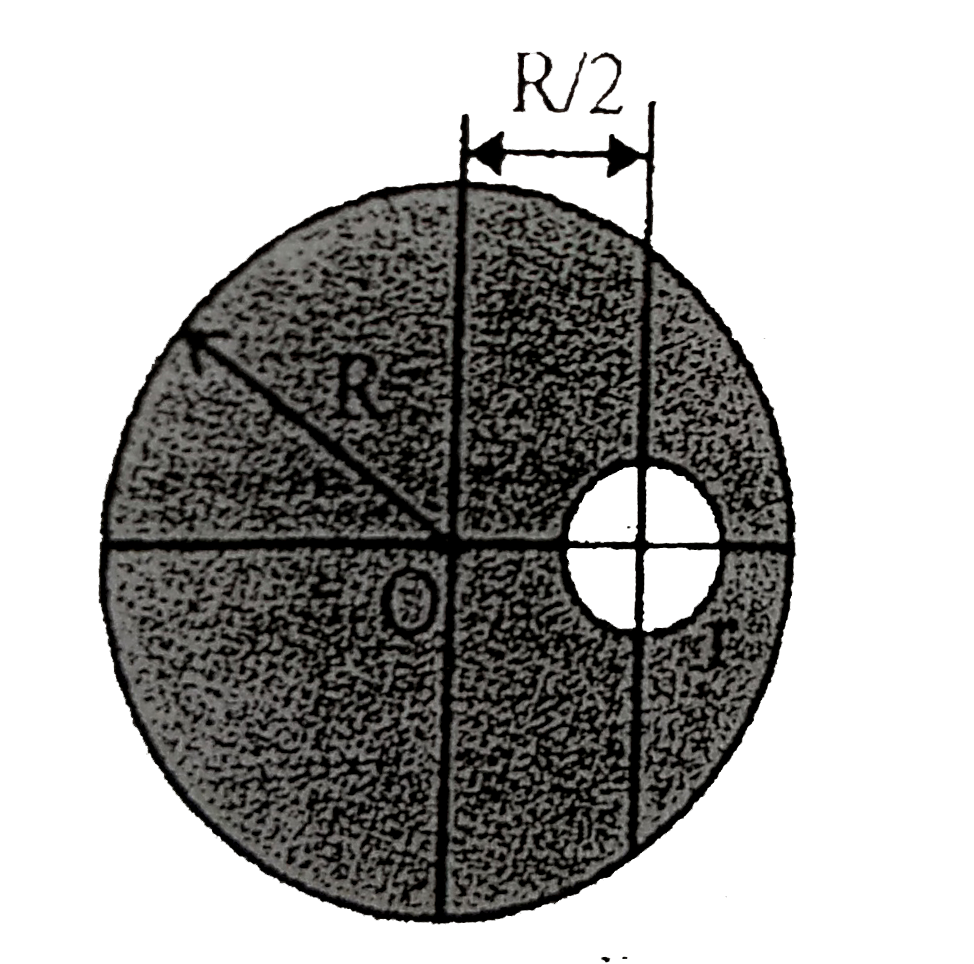
A paper disc of radius R from which a hole of radius r is cut out, is floating n liquid of surface tension, T. What will be force n the disc due to surface tension?
T=FL=F2π(R+r) ∴ F=2π(R+r)T
Topper's Solved these Questions
- SURFACE TENSIONBOOK - MOTIONCHAPTER - SURFACE TENSIONEXERCISE - SOLVED EXAMPLE
7 Videos
- SURFACE TENSIONBOOK - MOTIONCHAPTER - SURFACE TENSIONEXERCISE - Exercise - 1 Objective Problems | NEET
47 Videos
- SOUND WAVESBOOK - MOTIONCHAPTER - SOUND WAVESEXERCISE - Exercise - 3 (Section - B)
14 Videos
- SURFACE TENSION & VISCOSITY BOOK - MOTIONCHAPTER - SURFACE TENSION & VISCOSITY EXERCISE - Exercise - 4 | Level-II Previous Year | JEE Advanced
12 Videos
Similar Questions
A paper disc of radius R from which a hole of radius r is cut out, is floating in a liquid of surface tension, T. What will be force on the disc due to surface tension?
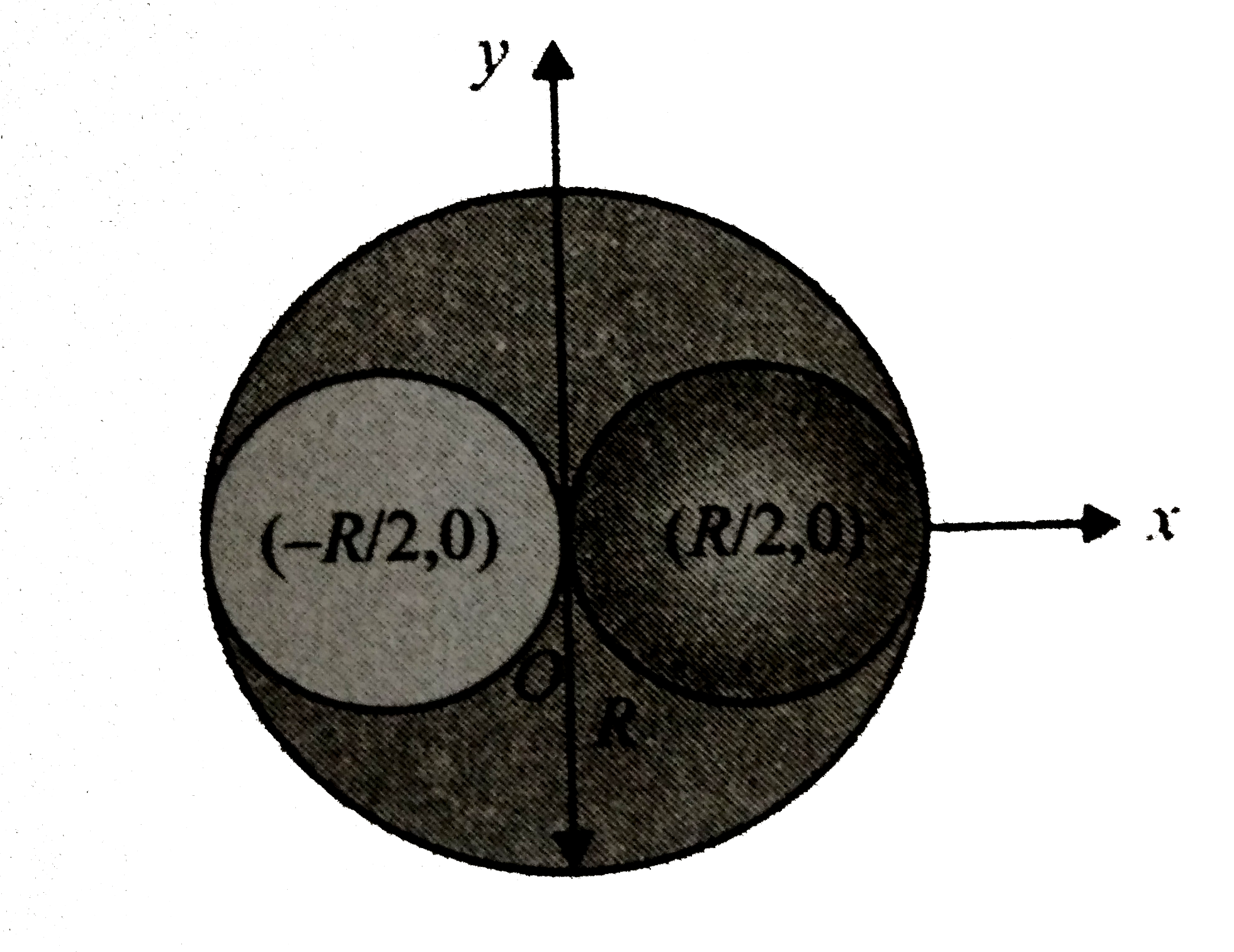
View SolutionFigure shows a uniform disc of radius R, from which a hole of radius R2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.
View Solution
Knowledge Check
A paper disc of radius R from which a hole of radius r is cut out is floating in a liquid of the surface tension S. The force on the disc due to the surface tension is
AS×2πRBS×2πrCS×2π(R−r)DS×2π(R+r)A disc of radius R has a concentric hole of radius r. It is floating on a liquid of surface tension T . What is the force of surface tension on the disc ?
A4π(R+r)TB4π(R−r)TC2π(R−r)TD2π(R+r)TFind the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
A square wire frame of side / is floating on the surface of liquid of surface tension T. The force required to pull out the frame from the liquid is
View SolutionA capillary tube of radius r is lowered into a liquid of surface tension T and density ρ. Given angle of contact =0∘.
The work done by surface tension will be
View SolutionThe excess pressure inside the drop of a liquid of surface tension T and radius of drom r is
View SolutionA disc of paper of radius R is floating on the surface of water of surface tension T . If r=20 cm and T=0.070N//m , then the force of surface tension on the disc is
View SolutionA needle of length l and density ρ will float on a liquid of surface tension σ if its radius r is less than or equal to:
View Solution
