A small sphere is moving at a constant speed in a vertical circle. Below is list of quantities that could be used to describe some aspect of the motion of the sphere.
I-kinetic energy
II- gravitational potential energy
III- momentum
Which of these quantities will change as this sphere moves around the circle ?
I and II only
I and III only
III only
II and III only
The correct Answer is:D
Step by step video, text & image solution for A small sphere is moving at a constant speed in a vertical circle. Below is list of quantities that could be used to describe some aspect of the motion of the sphere. I-kinetic energy II- gravitational potential energy III- momentum Which of these quantities will change as this sphere moves around the circle ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 2 (Level-I)
Explore 40 Videos
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 2 (Level-II)
Explore 28 Videos
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 4 Level-II
Explore 20 Videos
- Capacitance Book:MOTIONChapter:Capacitance Exercise:EXERCISE -4 LEVEL II
Explore 19 Videos
- CIRCULAR MOTIONBook:MOTIONChapter:CIRCULAR MOTIONExercise:EXERCISE - 4
Explore 16 Videos
Similar Questions
A small creature moves wilth constant speed in a vertical circle on a bright day. Does its shadow formed by the sun on horizontal plane move in a simple harmonic motion?
View SolutionA satellite is moving with a constant speed 'V' in a circular orbit about the earth. An object of mass 'm' is ejected from the satellite such that it just escapes form the gravitational pull of the earth. At the tme of its ejection, the kinetic energy of the object is
View Solution
Knowledge Check
A particle of mass m is moving with constant speed in a vertical circle in X−Z plane. There is a small both at some distance on Z−axis. The maximum distance of the shadow of the particle on X−axis from origin equal to :−
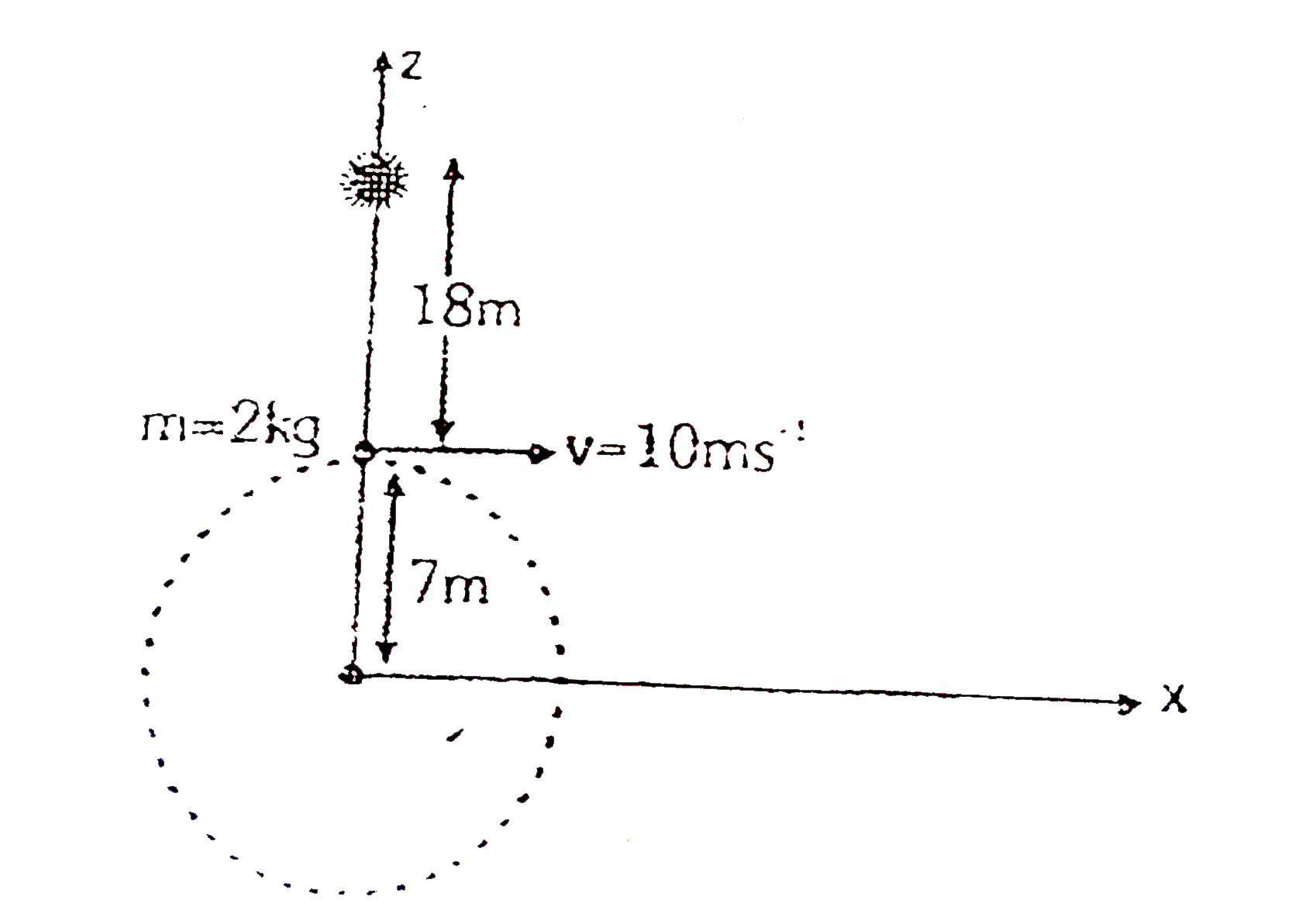 A17524mB12524mC25mD24m
A17524mB12524mC25mD24mA satellite is moving with a constant speed v in circular orbit around the earth. An object of mass ‘2m’ is ejected from the satellite such that it just escapes from the gravitational pull of the earth. At the time of ejection, the kinetic energy of the object is:
A12mv2B32mv2C2mv2Dmv2
A sphere of mass m rolls on a plane surface.Find its kinetic energy t an instant when its centre moves with speed v.
View SolutionA star like the sun has serveral bodies moving around it at different distance. Consider that all of them are moving in circular orbits. Let r be the distance of the body from the centre of the star and let its linear velocity be υ, angular velocity ω, kinetic energy K, gravitational potential energy U, total energy E and angular momentum L. As the radius r of the orbit increase, determine which of the above quantities increase and which ones decrease.
View SolutionIn the List-I below, four different paths of a particle are given as functions of time. In these functions, and are positive constants of appropriate dimensions and . In each case, the force acting on the particle is either zero or conservative. In List-II, five physical quantities of the particle are mentioned: is the linear momentum, is the angular momentum about the origin, is the kinetic energy, is the potential energy and is the total energy. Match each path in List-I with those quantities in List-II, which are conserved for that path.
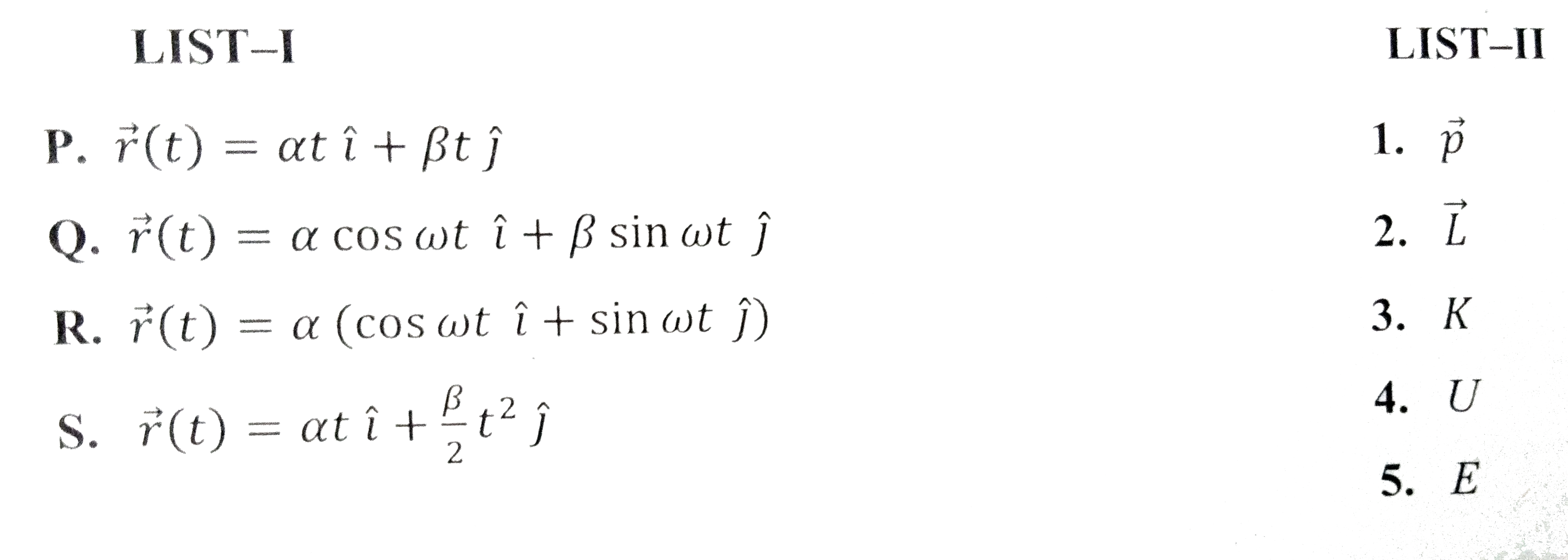
View SolutionA sphere moving with a velocity v0 on a smooth surface suddenly enters on a rough horizontal surface as shown in Fig. State which of the following statements are true or false
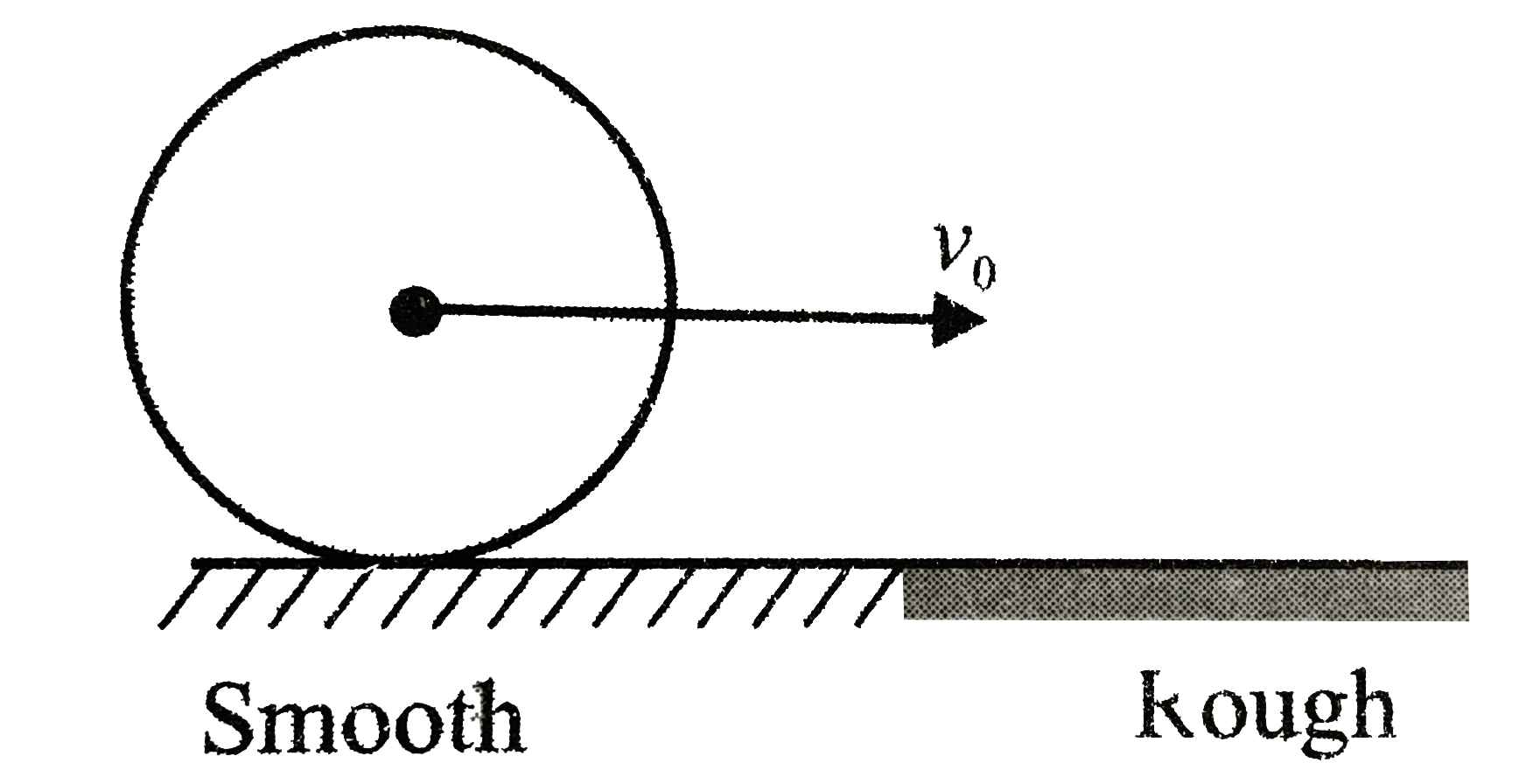
a. The sphere loses translational kinetic energy and gains rotational kinetic energy.
b. The total energy of the sphere is conserved.
c. The angular momentum of the sphere about any point OD the surface is conserved.
d. The final velocity attained by the centre of mass is 2v0/3.
View SolutionA uniformly charged sphere has charge Q. An electron (charge – e, mass m) revolves around it in a circular orbit of radius r. (a) Write the total energy (i.e., sum of its kinetic energy and electrostatic potential energy in the field of the sphere) of the electron. (b) If the time period of revolution of the electron in circular orbit of radius r is T, then find the time period if the orbital radius is made 4r.
View SolutionIn deep space, sphere A of mass 20 kg is located at the origin of an x axis and sphere B of mass 10 kg is located on the axis at x = 0.95 m. Sphere B is released from rest while sphere A is held at the origin. (a) What is the gravitational potential energy of the two-sphere system just as B is released? (b) What is the kinetic energy of B when it has moved 0.15 m toward A?
View Solution

