A Wireframe is made of a wire or uniform crosssection. which is shown in figure ABC. HGF and DIE are semicircular arcs of redius r. CD=DO=OE=EF=r and 'O' is the centre of circle. Then centre of mass of frame is:
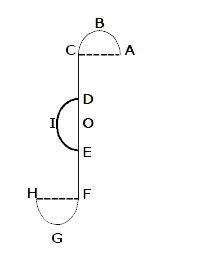
At distance towards left of O
At distance towards right of O
At distance towards left of O
At distance towards right of O
The correct Answer is:A
Step by step video & image solution for A Wireframe is made of a wire or uniform crosssection. which is shown in figure ABC. HGF and DIE are semicircular arcs of redius r. CD=DO=OE=EF=r and 'O' is the centre of circle. Then centre of mass of frame is: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 2 (Level-I)
Explore 40 Videos
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 2 (Level-II)
Explore 28 Videos
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 4 Level-II
Explore 20 Videos
- Capacitance Book:MOTIONChapter:Capacitance Exercise:EXERCISE -4 LEVEL II
Explore 19 Videos
- CIRCULAR MOTIONBook:MOTIONChapter:CIRCULAR MOTIONExercise:EXERCISE - 4
Explore 16 Videos
Similar Questions
Knowledge Check
A wire of uniform cross-section is bend in the shape shown in figure. The co-ordinate of the centre of mass of each side are shown in (figure). The co-ordinates of the centre of mass of the system are.
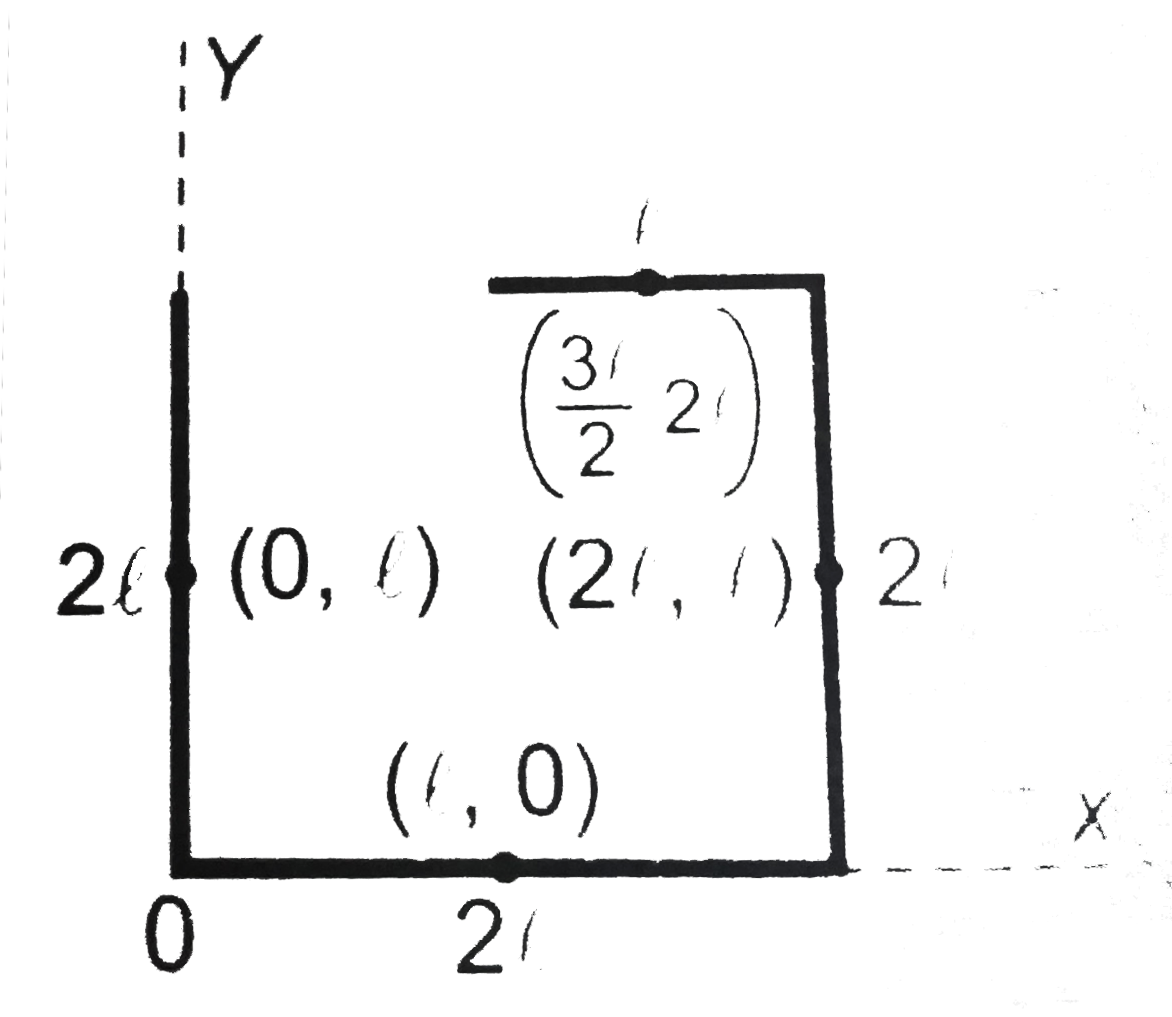 .A(15l14,6l7)B(15l14,l)C(l,l2)D(l,l)
.A(15l14,6l7)B(15l14,l)C(l,l2)D(l,l)In the figure shown a hole of radius 2 cm is made in a semicircular disc of radius 6π at a distance 8 cm from the centre C of the disc. The distance of the centre of mass of this system from point C is :
 A4 cmB8cmC6 cmD12 cm
A4 cmB8cmC6 cmD12 cmA current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
 Aμ04.irBμ02πrCμ0I2πrDμ0I8πr(3π+4)
Aμ04.irBμ02πrCμ0I2πrDμ0I8πr(3π+4)
Find the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionFind the coordination of the centre of mass of a uniform semicircular wire of radius R and mass M.
View Solution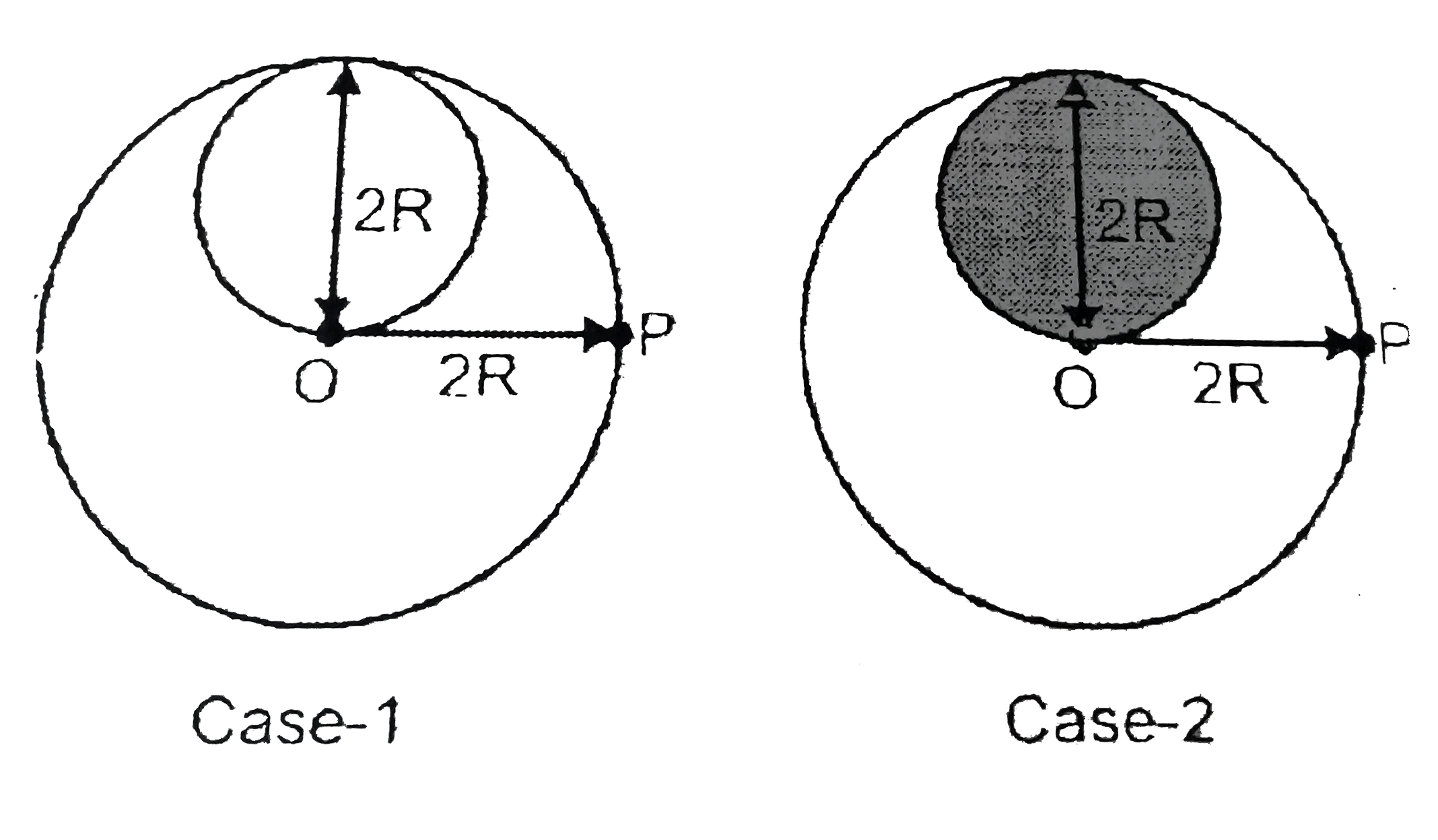
A lamina is made by removing a small disc of diameter 2 R from a bigger disc of uniform mass density and radius 2R, as shown in figure. A second similar disc is made but instead of hole a disc of triple the density as of first it filled in the hole. Centre of mass is calculated in both the cases and was found at a distance r1&r2 from centre O respectively find the ratio ∣∣∣2r2r1∣∣∣
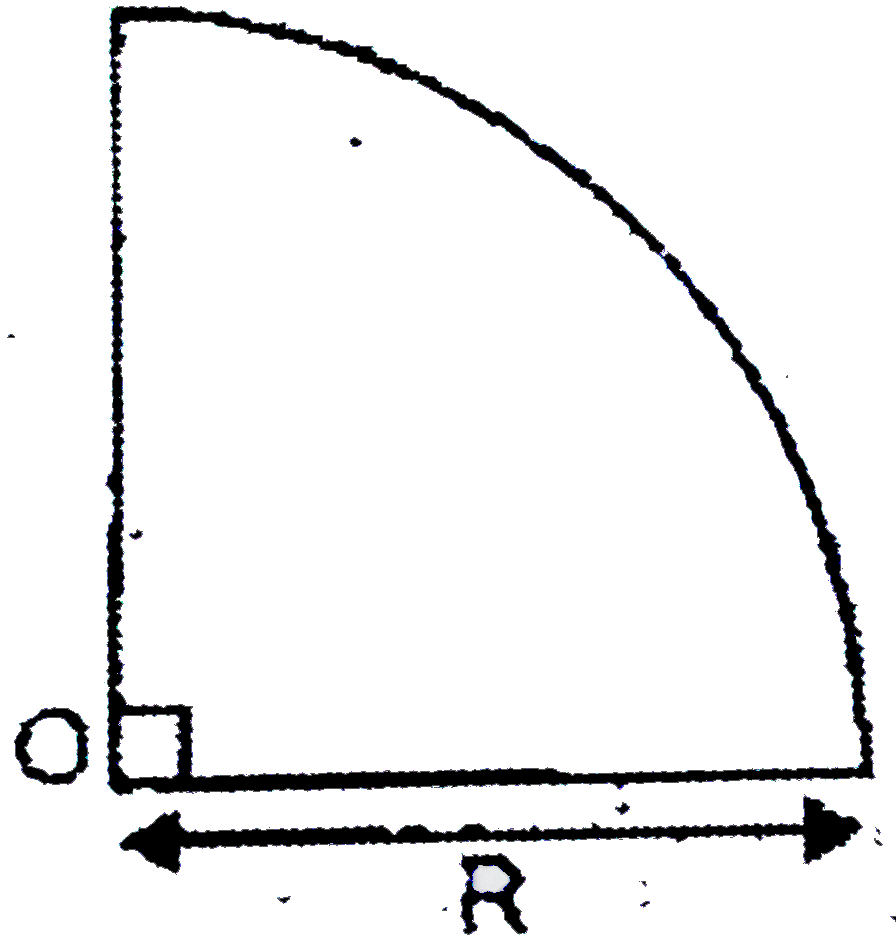
View SolutionIn the figure one fourth part of a uniform disc of radius R is shown. The distance of the centre of mass of this object from centre 'O' is :
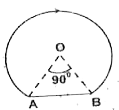
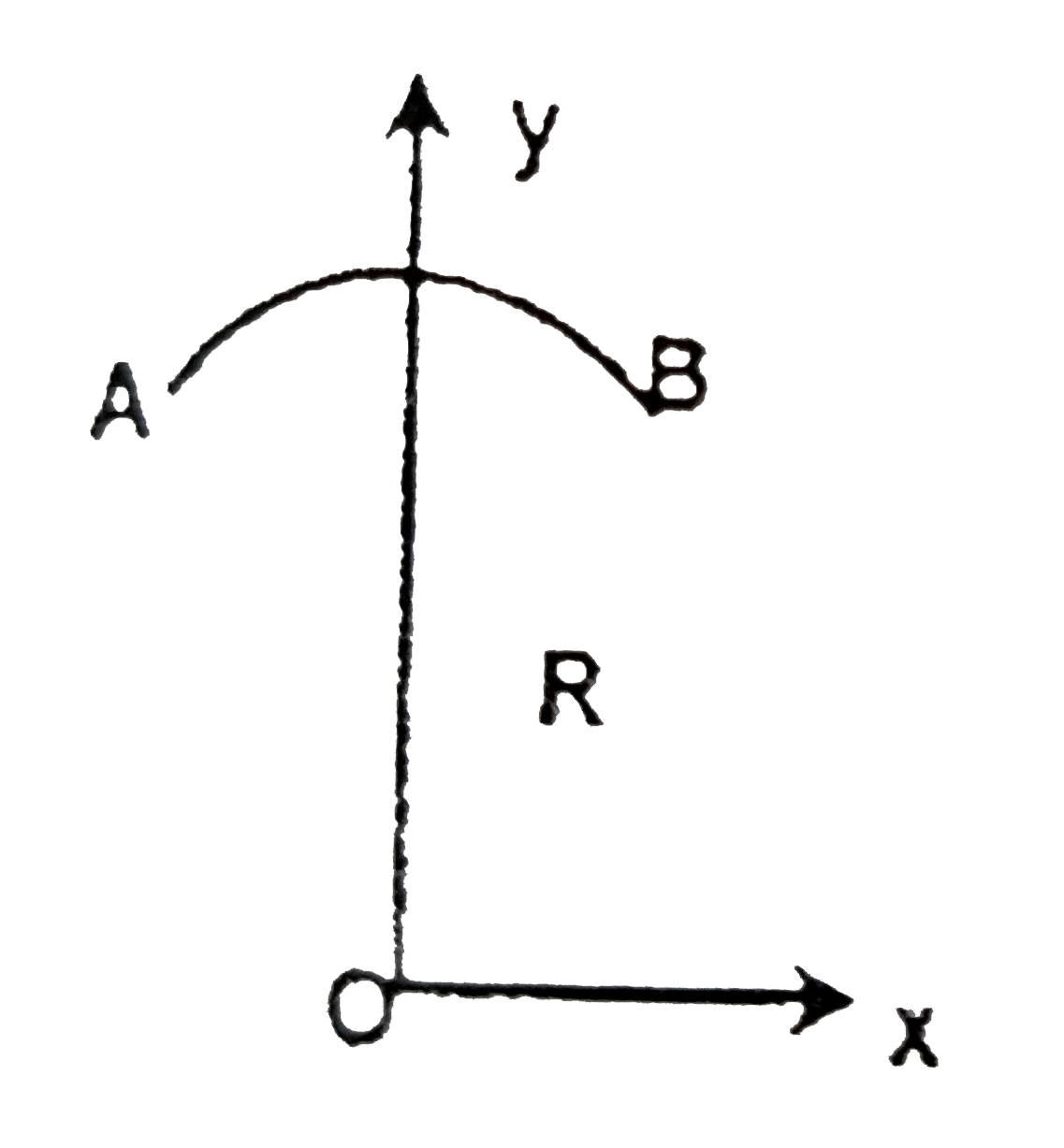
View SolutionA circular are (AB) of thin wire frame of radius R and mass M makes an angle of 90∘ at the origin.The centre of mass of the arc lies at
View Solution