A pendulum of mass m and length l is released from rest in a horizontal position. A nail, a distance d below the pivot, causes the mass to move along the path indicated by the dotted line. The minimum distance such that the mass will swing completely round in the circle shown in figure is d then 5dL is
2
3
4
5
The correct Answer is:2
√2gl=√5g(l−a)⇒2l=5l−5d
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A pendulum bob of mass m and length L is released from angle θ with the vertical. Find
(a) the speed of the bob at the bottom of the swing and
(b) tension in the string at that timeView SolutionA thin rod of mass M and length L is released from rest in position shown. The path of centre of mass of rod till the rod become horizontal is [ Assume surface is smooth]
_PHY_208_Q01.png)
View Solution
Knowledge Check
- Question 1 - Select One
A rod of mass m and length l is hinged at 'its' end and released from rest in position shown. Find the force exerted by the hinge when the rod becomes horizontal
Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14 - Question 2 - Select One
A simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
AmL√2gLBmL√gLCmL√3gLDnone - Question 3 - Select One
A simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle α. A pin is located at a distance l below the pivot point. When the pendulum swings down, the string hits the pin as shown in figure. The maximum angle θ which the string makes with the vertical after hitting the pin is
A(a) cos−1[Lcosα+lL+l]B(b) cos−1[Lcosα+lL−l]C(c) cos−1[Lcosα−1L−l]D(d) cos−1[Lcosα−1L+l]
A rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA thin plank of mass m and length l is pivoted at one end and it is held stationary in horizontal position by means of a light thread as shown in the figure then find out the force on the pivot.
View SolutionA bob tied to an ideal string of length l is released from the horizontal position shown. A peg P whose height is adjustable, can arrest the free swing of the pendulum, as shown in Figure.
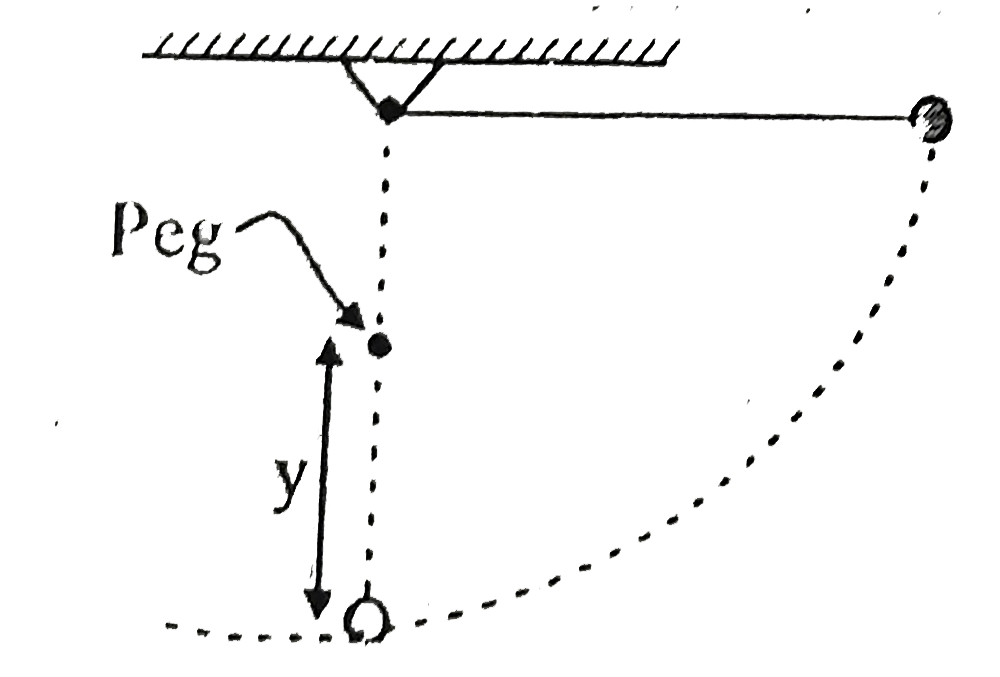View SolutionA particle of mass m attached to the end of string of length l is released from the horizontal position. The particle rotates in a circle about O as shown When it is vertically below O, the string makes contact with a nail N placed directly below O at a distance h and rotates around it. For the particle to swing completely around the nail in a circle.
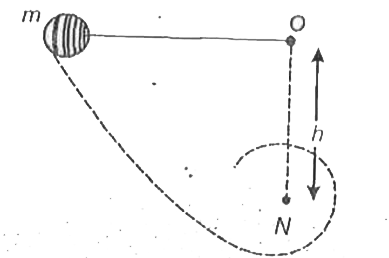View SolutionOne end of a uniform rod of length l and mass m is hinged at A. It is released from rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes vertical is
View Solution