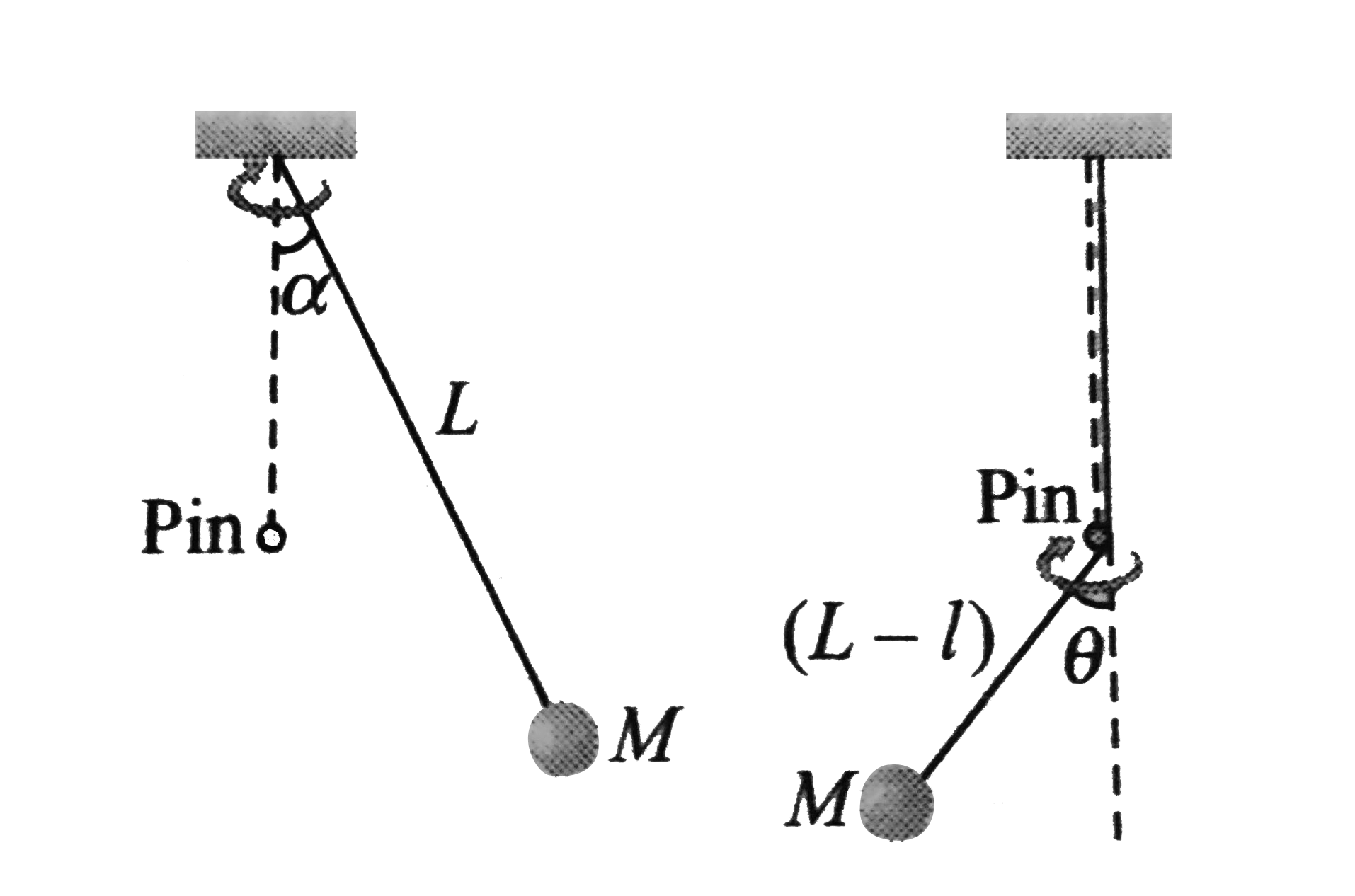
A simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle α. A pin is located at a distance l below the pivot point. When the pendulum swings down, the string hits the pin as shown in figure. The maximum angle θ which the string makes with the vertical after hitting the pin is
(a) cos−1[Lcosα+lL+l]
(b) cos−1[Lcosα+lL−l]
(c) cos−1[Lcosα−1L−l]
(d) cos−1[Lcosα−1L+l]
The correct Answer is:C
Since the pendulum started with no kinetic energy, conservation of energy implies that the potential energy at Qmax must be equal to the original potential energy, i.e., the vertical position will be same. Therefore,
Lcosα=l+(L−l)cosθ
⇒cosθ=Lcosα−1L−1
⇒θ=cos−1[Lcosα−1L−1]
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Subjective
Explore 23 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A simple pendulum consists of a ball of mass m connected to a string of length L. The ball is pulled aside so that the string makes an angle of 53∘ with the verticle and is released. Find the ratio of the minumum and the tension in the string.
View SolutionA ball A of mass m attached to a string of length L is released when the string is horizontal. It strikes another ball B of mass 2m suspended to another string of length L at rest as shown. Find the maximum angle made by the string if the collision is completely inelastic.
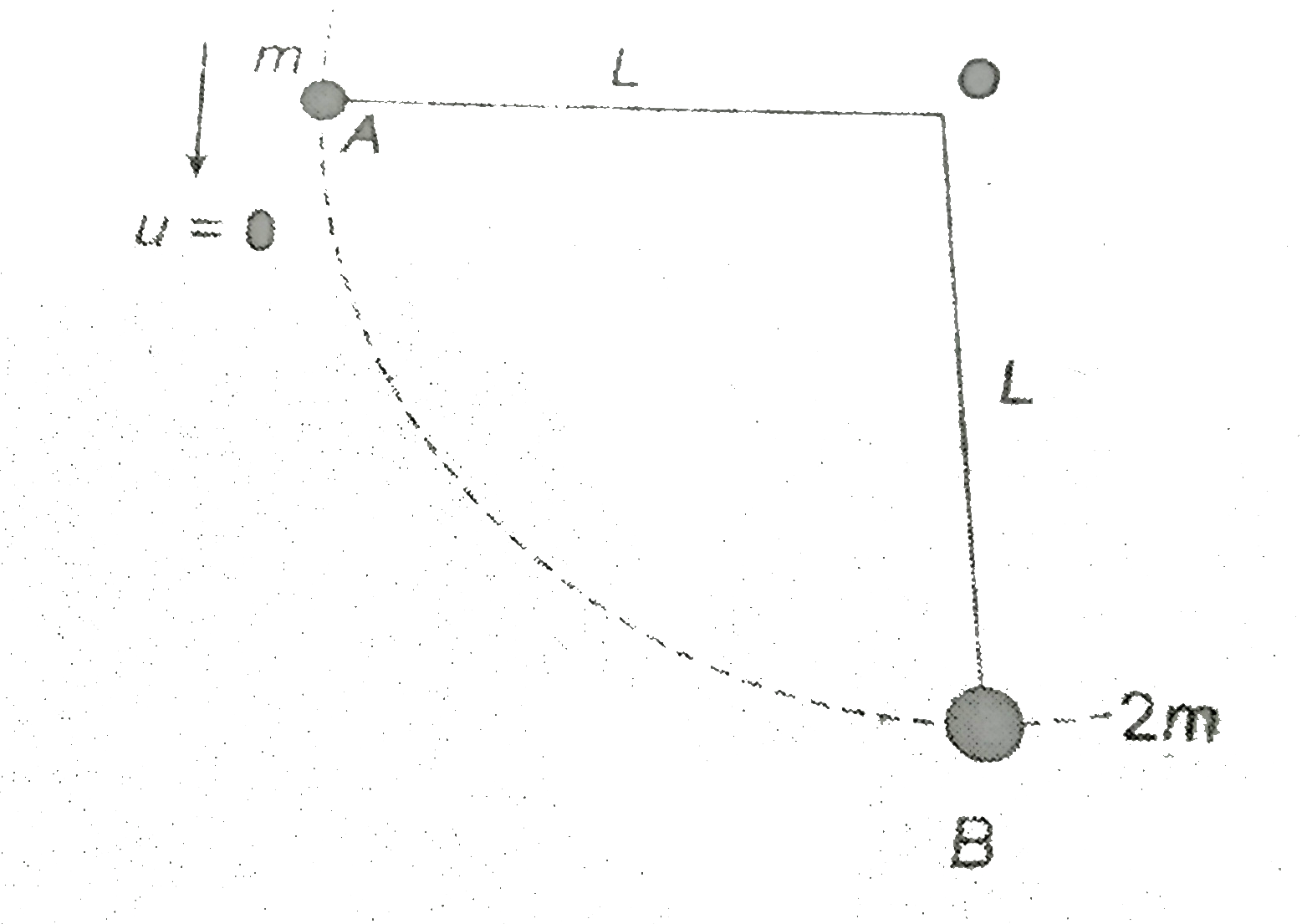
View Solution
Knowledge Check
A pendulum consists of a small mass m at the end of a string of length L. The pendulum is pulled aside making an angle θ with the vertical and released. Taking the suspension point as the axis, at the instant of release
Atorque on the pendulum is mgL cosθBtorque on the pendulum is mgL sinθCangular acceleration of pendulum is gcosθLDangular acceleration of pendulum is gsinθLA body of mass m is tied to a string of length l and whirled in a verticle cirlce. The velocity of the body at the lowest position is u. Then the tension in the string at a position when the string makes an angle θ with the vertical is
Amu2lBmu2l+mgcosθCmu2l+mg(2cosθ−3)Dmu2l+mg(3cosθ−2)A pendulum of mass m and length l is released from rest in a horizontal position. A nail, a distance d below the pivot, causes the mass to move along the path indicated by the dotted line. The minimum distance such that the mass will swing completely round in the circle shown in figure is d then 5dL is
 A2B3C4D5
A2B3C4D5
A bob tied to an ideal string of length l is released from the horizontal position shown. A peg P whose height is adjustable, can arrest the free swing of the pendulum, as shown in Figure.
View SolutionA pendulum bob of mass m and length L is released from angle θ with the vertical. Find
(a) the speed of the bob at the bottom of the swing and
(b) tension in the string at that time
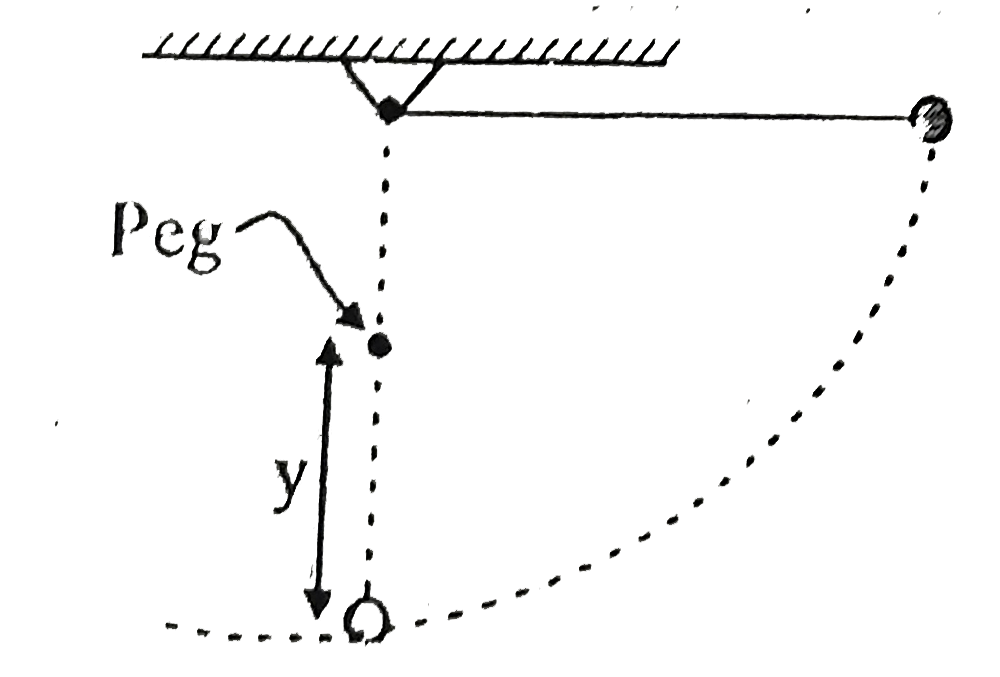
View SolutionA pendulum, comprising a light string of length L and a small sphere, swings in a vertical plane. The string hits a peg located a distance d below the point of suspension as shown in the figure. If the pendulum is released from the horizontal position (θ=90∘) and is to swing in a complete circle centered on the peg, then the minimum value of d is kL. Find k :
'(##CEN_KSR_PHY_JEE_C07_012_Q06##)'
View SolutionA particle of mass m is attached to a string of length L and given velocity √10hL in the horizontal direction at the lowest point. Find tension in the string when the particle is at (a) (i) lowest position (ii) highest position, (b) when the string makes an angle 60∘ with (i) lower vertical and (ii) upper vertical.
View SolutionA pendulum comprising a light string of length L and small sphere, swings in the vertical plane . The string hits a peg located a distance of bellow the point of suspension (figure). If the pendulum is released from rest at the horizontal possition (θ=90∘) and is to swing in a complete circule centered on the peg, the minimum value of d is

View Solution

