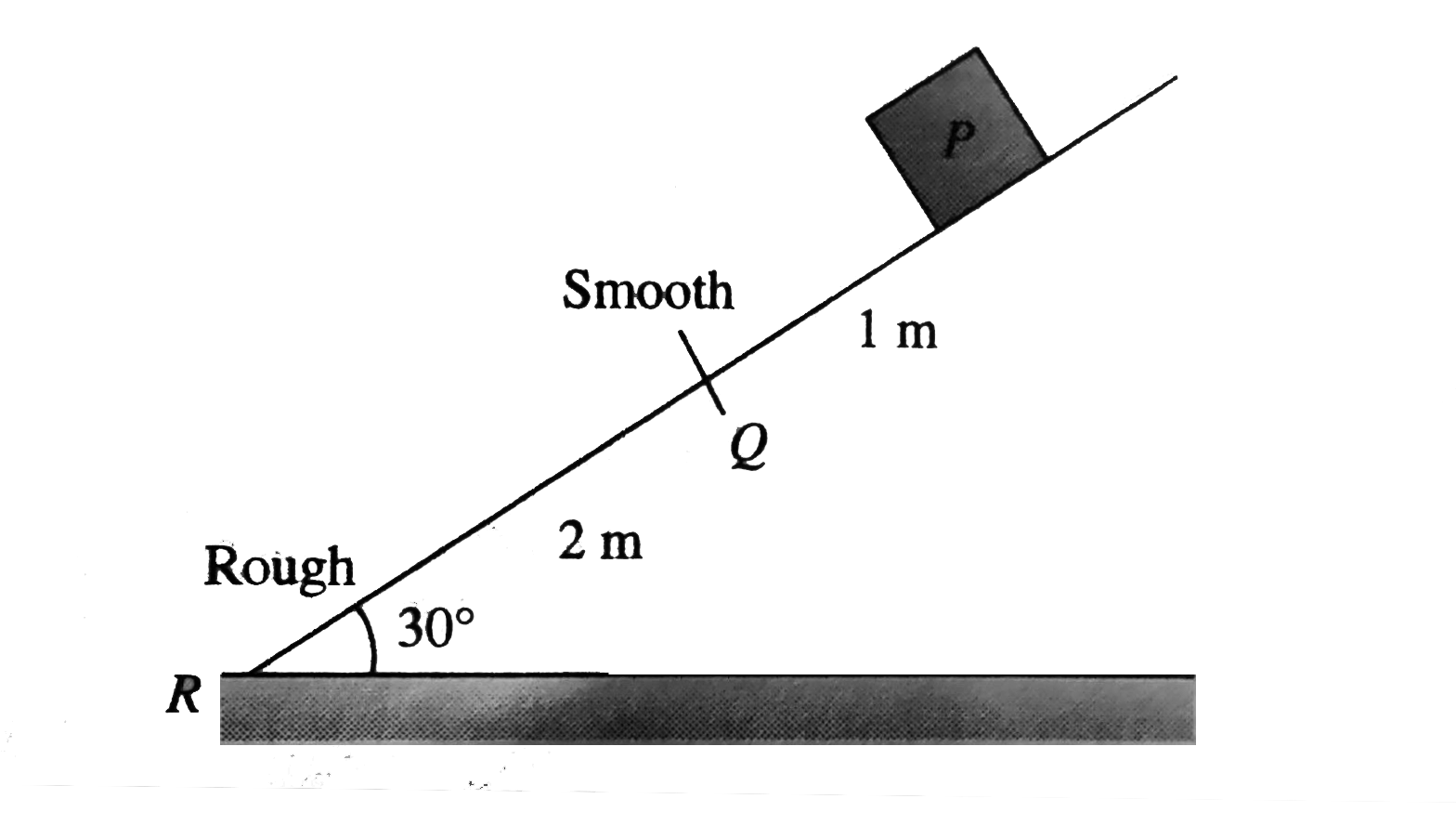
A block of mass 5.0kg slides down from the top of an inclined plane of length 3m. The first 1m of the plane is smooth and the next 2m is rough. The block is released from rest and again comes to rest at the bottom of the plane. If the plane is inclined at 30∘ with the horizontal, find the coefficient of friction on the rough portion.
(a) 2√3
(b) √32
(c) √34
(d) √35
The correct Answer is:B
Force method:
From P to Q: v2=02+2a1s1
where a1=gsin30∘, s1=1m
and from Q to R: 02=v2+2a2s2
where a2=gsin30∘−μgcos30∘, s2=2m
solve to get μ=√3/2
Work-energy method:

In terms of energy considerations you can summarize the whole process as loss in gravitational potential energy of the block=work done against friction, or
(mg)×(3sin30∘)=(μmgcosθ)×2
3×1/2μ×√32⇒μ=√32
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Subjective
Explore 23 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A body is released from rest from the top of an inclined plane of length L and angle of inclination θ ,.The top of plane of length LN (N>1) is smooth and the remaining part is rough.If the body comes to rest on reaching the bottom of the plane, then the value of coefficient of friction of rough surface is ?
View SolutionThe upper portion of an inclined plane of inclination α is smooth and the lower portion is rough. A particle slides down from rest from the top and just comesto rest at the foot.If the ratio ofthe smooth length to rough length is w : find the coefficient of friction.
View Solution
Knowledge Check
A block of mass m is released from the top of a mooth inclined plane of height h its speed at the bottom of the plane is proportion to
Am0BmCm2Dm−1What is the time required for a block to slide down from the top to the bottom ofan inclined plane 6.4 m long if the inclination of the plane with the horizonta l is 30° and the coefficient of friction= 0.2?
A2sB1.5sC3sD2.5sAn object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1
The upper portion of an inclined plane of inclination a is smooth and the lower portion is rough. A partical slide down from rest the top and just comes to rest at the foot . If the ratio of smooth length to rough length is m:n, find the coefficient of friction .
View SolutionIf the body starts from rest from the top of the rough inclined plane of length 1, time taken to reach the bottom of the plane is
View Solution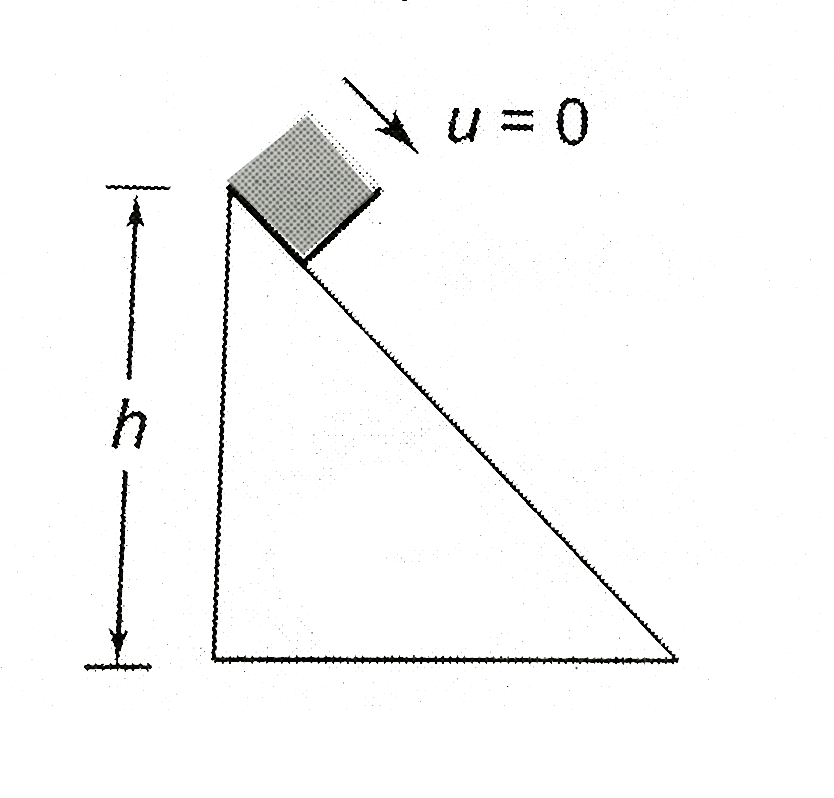
A block is released from the top of the smooth inclined plane of height h. Find the speed of the block as it reaches the bottom of the plane.
View SolutionThe upper portion of an incline plane of inclination α is smooth and the lower portion is rough. A particle slides down from rest from the top and just comes to rest at the fool. If the ratio of the smooth length to rough length is 2:1 and coefficient of frection is n tanα, then write the value of n.
View SolutionThe upper half of an inclined plane of inclination 45∘ is perfectly smooth while the lower half is rough. A block starting from rest at the top comes back to rest at the bottom. The coefficient of friction for the lower half is
View Solution

