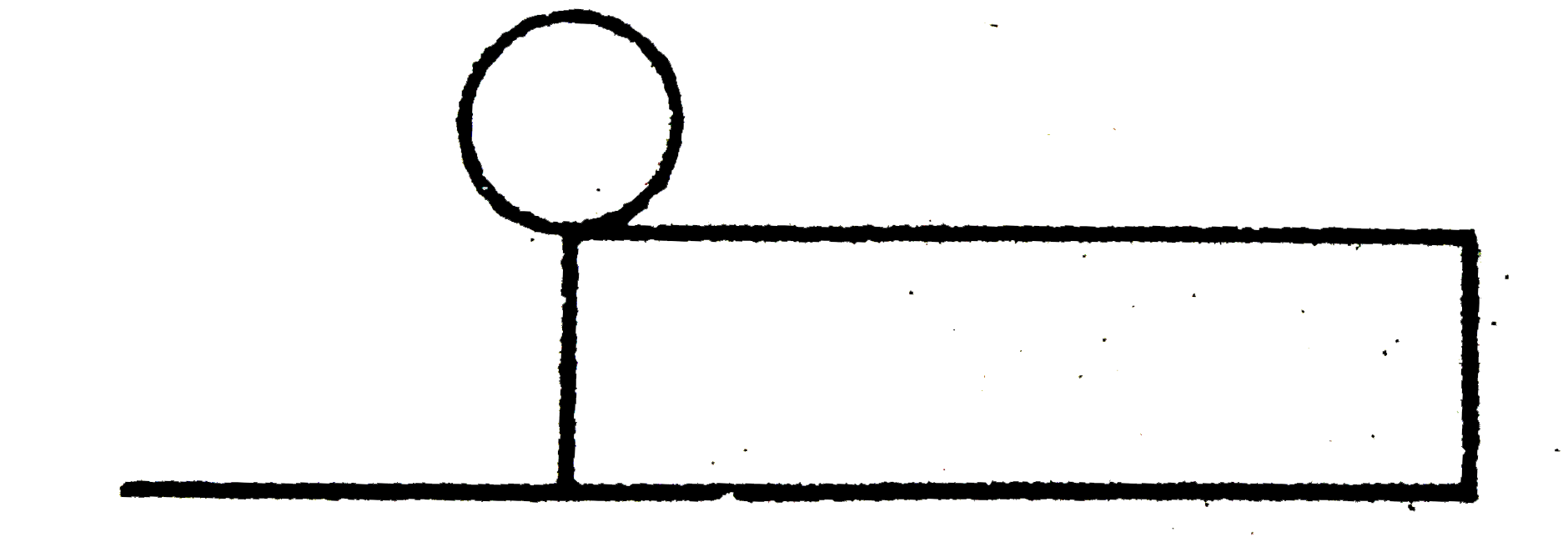
A cylinder of mass m is placed on the edge of a long plank of same mass kept on the smooth horizontal surface, where μ the is the coefficient of friction between cylinder and plank. The cylinder is given an impulse at t=0 which impacts it is velocity V0. find the time in which pure rolling starts.
V0/2μg
V0/4μg
V02√2μg
V0/4√2μg
The correct Answer is:2
Acceleration of plank, =ap=μg
αc=μmgR(mR2/2)

=2μgR
For pure rolling after t,
VP=VC−Rωc
αpt=(V0−aCt)−RαCt
or μgt=(V0−μgt)−2μgt
t=V0/4g
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
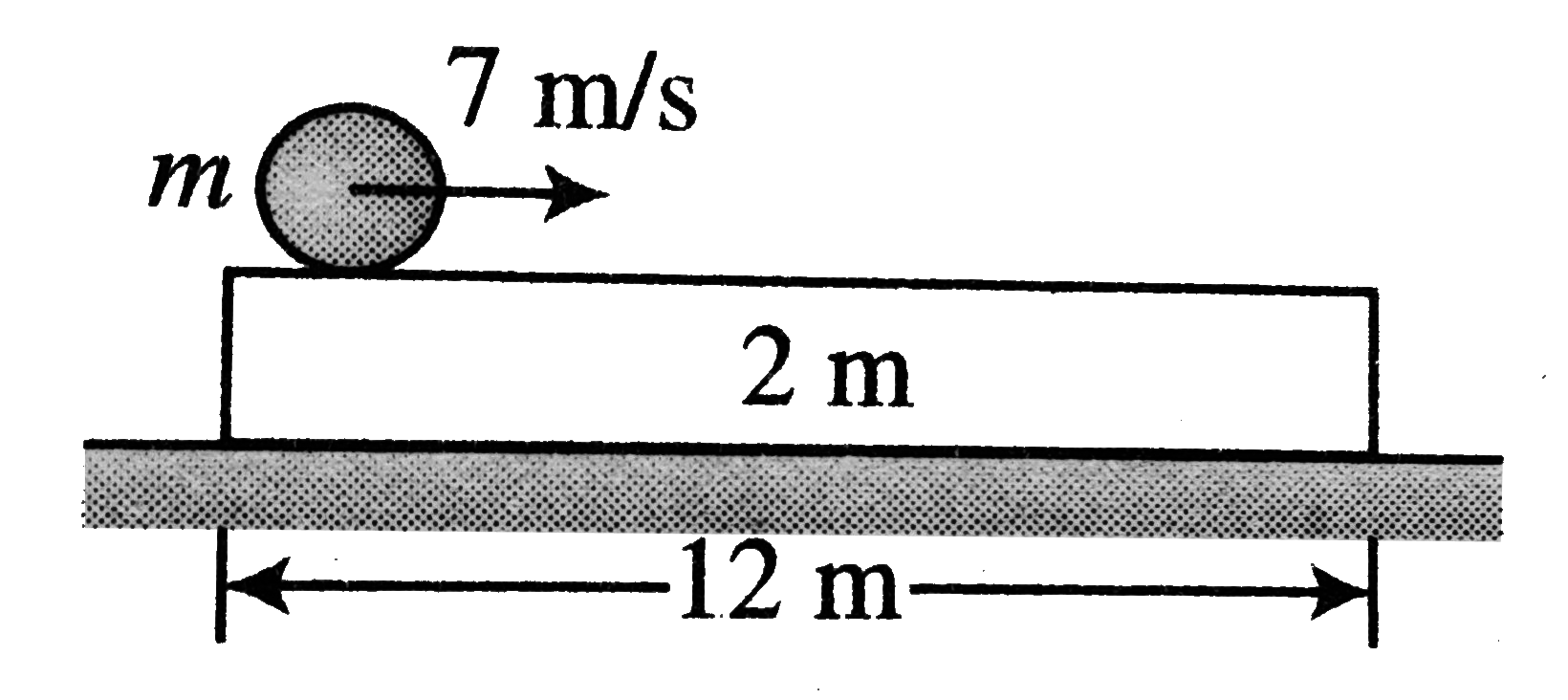
A cylinder of mass m is kept on the edge of a plank of mass 2m and length 12m, which in turn is kept on smooth ground. Coefficient of friction between the plank and the cylinder is 0.1. The cylinder is given an impulse, which imparts it a velocity 7ms−1 but no angular velocity. Find the time after which the cylinder falls off the plank.
View SolutionA solid cylinder is kept on one edge of a plank of same mass and length 25 m placed on a smooth surface as shown in the figure. The coefficient of friction between the cylinder and the plank is 0.5. The plank is given a velocity of 20ms−1 towards right. Find the time (in S) after which plank any cylinder will separate. [g=10ms−2]

View Solution
Knowledge Check
A block A of mass m is placed over a plank B of mass 2m. Plank B is placed over a smooth horizontal surface. The coefficient of friction between A and B is 12 block A is given a velocity v0 towards right. Accelration of B relative to A is
 Ag2BzeroC3g4Dg4
Ag2BzeroC3g4Dg4A block of mass m is placed gently onto a long plank of mass M moving with a velocity v0 on a smooth horizontal floor. If friction is present between M and m :
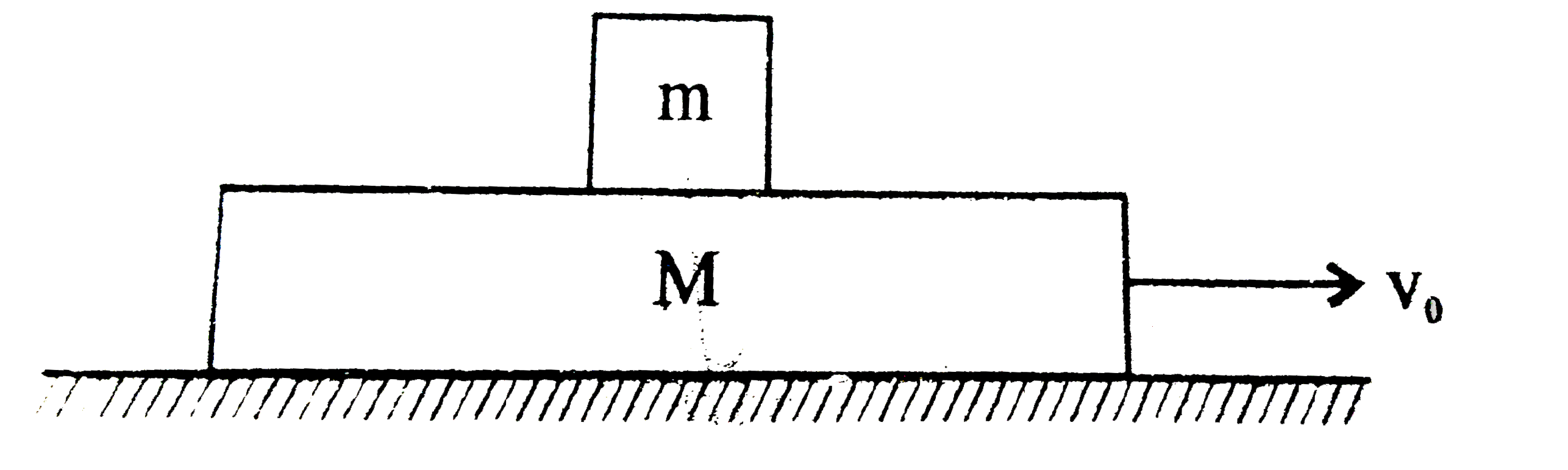 Avcentre of mass=Mv0M+mBWfriction on m is positiveCWFriction on M is negativeDfinal velocity of both =mv0m+M
Avcentre of mass=Mv0M+mBWfriction on m is positiveCWFriction on M is negativeDfinal velocity of both =mv0m+MA block A of mass m is over a plank B of mass 2m. Plank B si placed over a smooth horizontal surface. The coefficient of friction between A and B is 12. Blocks A is given a velocity V0 towards right. Then
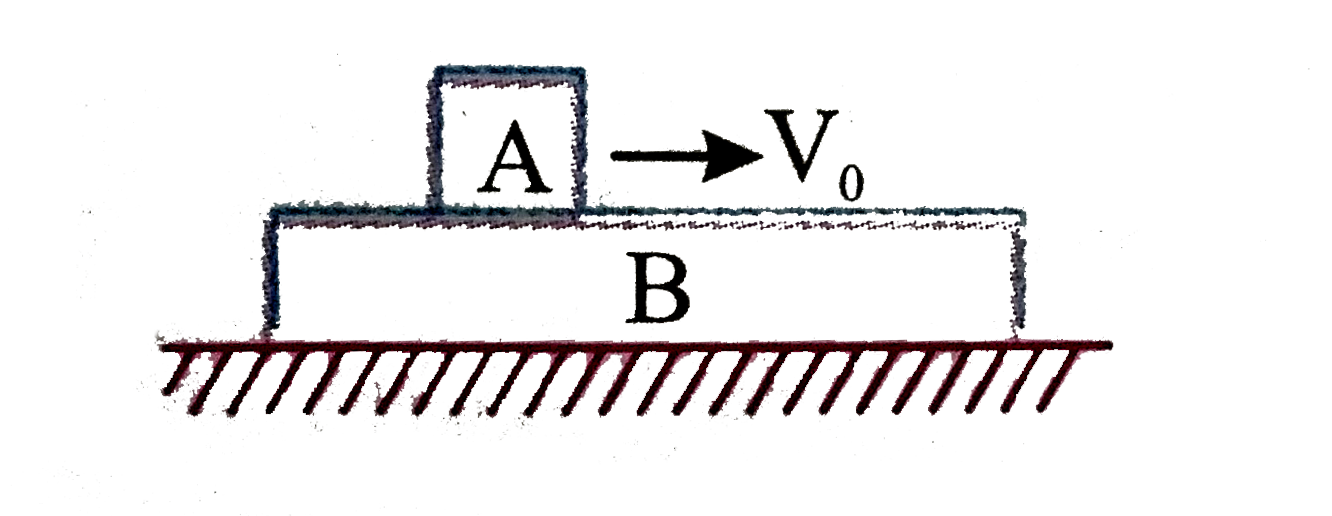 AAcceleration of A is g2BAcceleration of A is gCAcceleration of B relative to A is 34gDAcceleration of A is zero
AAcceleration of A is g2BAcceleration of A is gCAcceleration of B relative to A is 34gDAcceleration of A is zero
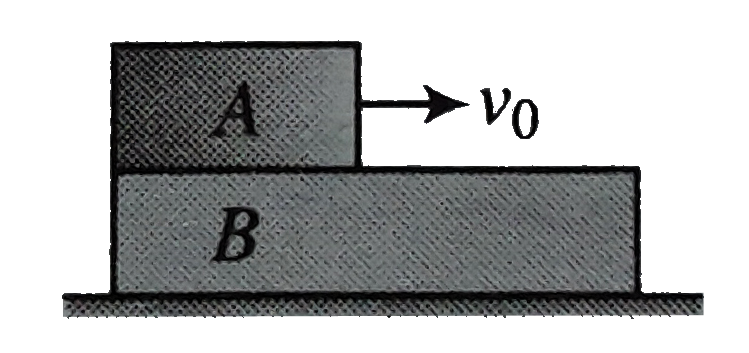
A block A of mass m is placed over a plankB of mass 2m plank B is placed over a smooth horizontal surface .The coefficient of friction between A and B is 0.4 Block A is given a velocity v0 toward right Find acceleration (in ms−2 of B relative to A
View SolutionIn the figure shown, a solid sphere of mass 'm' and radius r is released from a height 6r to slide down a smooth surface. A plank of same mass 'm' touches the horizontal portion of the surface at the ground. The co-efficient of friction between the plank and the sphere is μ and that between the plank and the ground is μ/4. Find the work done by the friction force between the plank and the ground till the sphere starts pure rolling on the plank. Neglect the height of the plank.

View SolutionA bar of mass m1 is placed on a plank of mass m2 which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t0 at which the plank starts sliding is :

View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
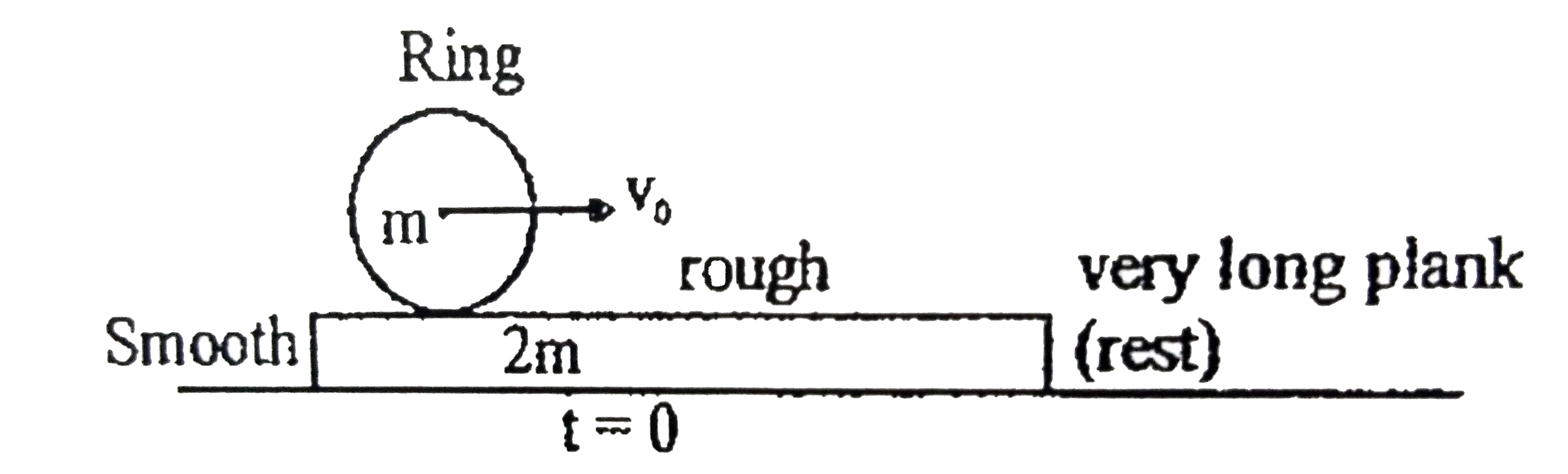
View SolutionA ring of mass m having velocity v0 is placed on a long plank lies on smooth horizontal surface at time t=0 as shown. Find the time when the ring start pure rolling on the plank. [μ is coefficient of friction between the ring and the plank.]
View Solution