The axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed $v_{1}$ . It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I

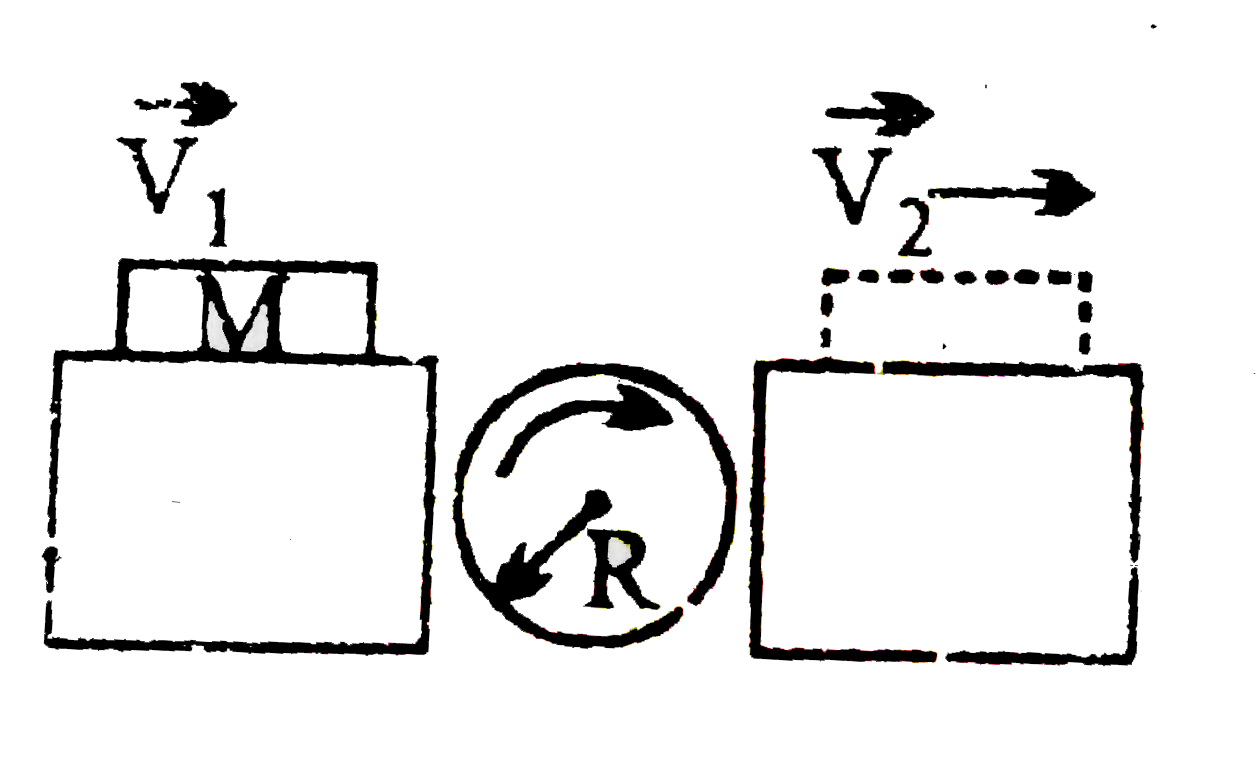
For the entire process the quantitiy (ies) which will remain conserved for the (cylinder+block) system is/ are (anuglar momentum is considered about the cylinder axis)

mechanical energy, momentum and angular momentum

mechanical energy & angular momentum only

momentum & angular momentum only

angular momentum only

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Answer

Step by step video, text & image solution for The axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed v_(1). It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I For the entire process the quantitiy (ies) which will remain conserved for the (cylinder+block) system is/ are (anuglar momentum is considered about the cylinder axis) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
The axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed $v_{1}$ . It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I

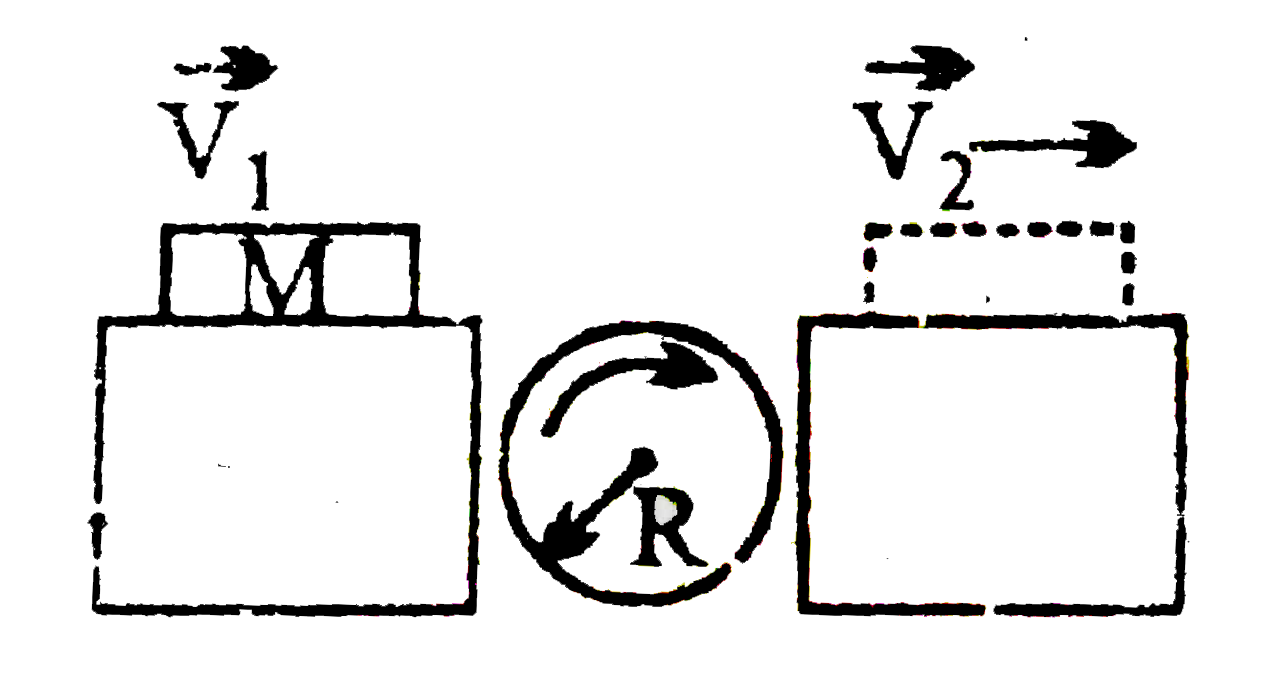
If $ω$ is final angular velocity of the cylinder, then
A $v_{1} = ω R$
B $v_{2} = ω R$
C $v_{1} < ω R$
Dnone
Question 2 - Select One
The axis of the uniform cylinder in figure is fixed. The cylinder is initially at rest. The block of mass M is initially moving to the friction and with speed $v_{1}$ . It passes over the cylinder to the dashed position. When it first makes contact with the cylinder, it slips on the cylinder, but the friciton is large enough so that slipping ceases before M loses contacts wtih the cylinder. the cylinder has a radius R and a rotaitonal intertia I

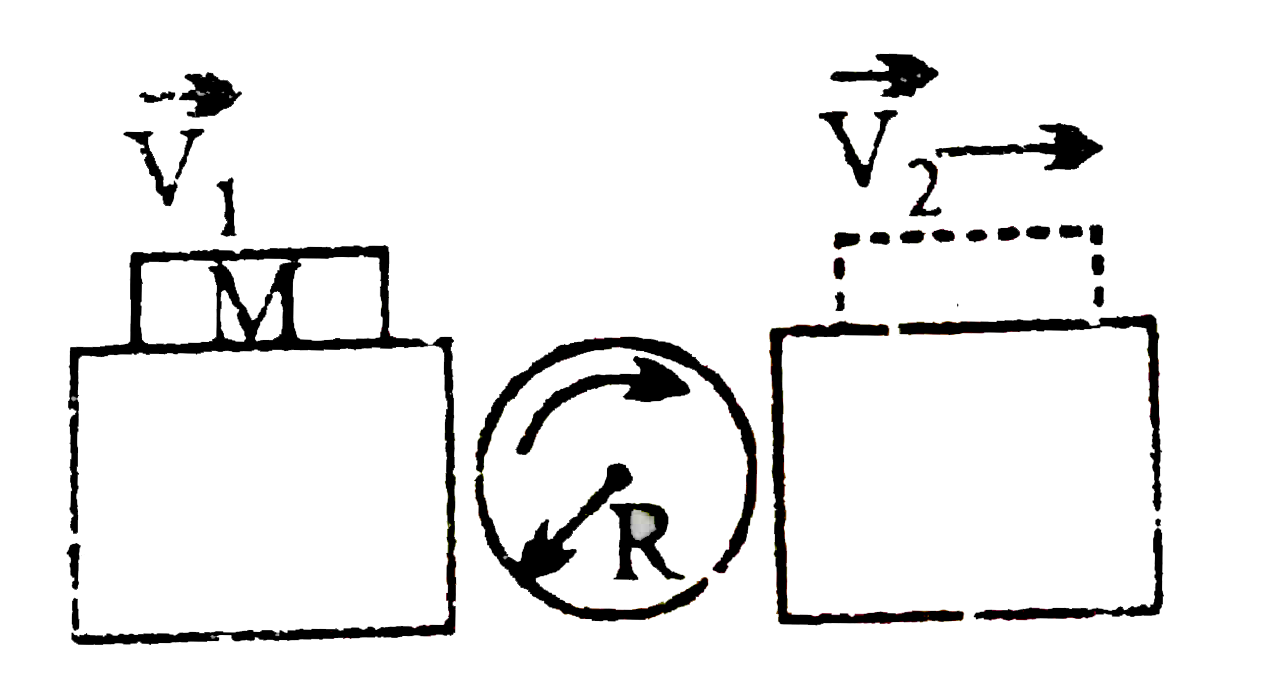
Assertion : Momentum of the block -cylinder system is conserved
Reason: Force of friction between block and cylinder is internal force of block -cylinder system.
AIf both (A) and (R) are true and (R) is the correct explanation of (A)
BIf both (A) and (R) are true but (R) is not correct explanation
C(if (A) is true but (R) is false
DIF (A) is false and (R) is true
Question 3 - Select One
A uniform disc of mass M and radius R is initially at rest. Its axis is fixed through O. A block of mass m is moving with speed $v_{1}$ on a frictionless surface passes over the disc to the dotted position. On coming in contact with the disc, it slips on it. The slipping ceases before the block loses contact with the disc, due to the high friction. Now, the velocity of mass m is

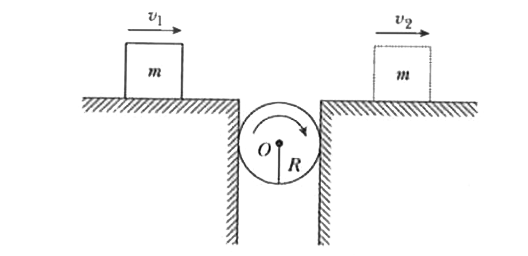A $v_{2} = \frac{v_{1}}{1 + (M / 2 m)}$
B $v_{2} = \frac{v_{1}}{2 M}$
C $v_{2} = \frac{v_{1}}{1 + (M / m)}$
D $v_{2} = 2 v_{1}$

BANSAL-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile

The correct Answer is:D

Topper's Solved these Questions

Similar Questions

Knowledge Check

BANSAL-TEST PAPERS-PHYSICS