In the arrangements as shown Mgt2m. Find the extension in the spring of forces constant K1. All pulleys are smooth and massless and the blocks do not oscillates.
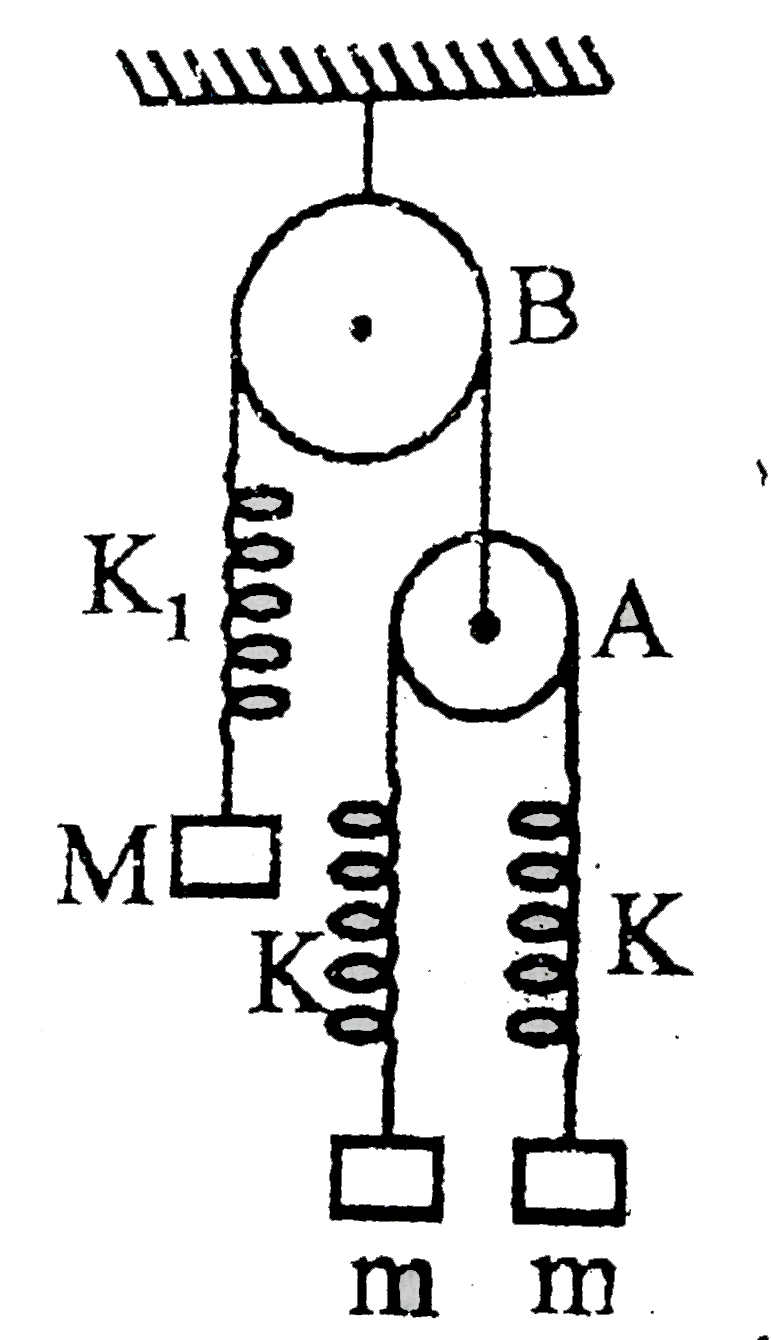
MmgK1(M+m)
(4Mmg).((M+m)).KK1
MmgK1(M+2m)
4MmgK1(M+2m)
The correct Answer is:4
a=(M−2m)g(M+2m)
Now, Mg−K1x1=Ma
x1=M(g−a)K1
=4MmgK1(M+2m)
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
In the arrangement shown, find the acceleration of each block, tension in the string and reaction in the pulley. The string and pulley are light (massless) (m1>m2). Neglect the friction in pulley.

View SolutionIn the device shown in Fig, the block m is displaced down slightly and released. It starts oscillating. Pulleys are smooth and massless string and springs are also massless. Find time period of oscillations.

View Solution
Knowledge Check
As shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be
 Ak1k2Bk1+k2C1k1+1k2Dk1k2k1+k2
Ak1k2Bk1+k2C1k1+1k2Dk1k2k1+k2In the adjoining figure, block A is of mass (m) and block B is of mass2 m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched.
 .AThe maximum extension of the spring is 4mgk.BThe speed of A when extension in spring is 2mgk is 2g√2m3k.CThe acceleration of block B when the extension in the spring is maximum, is 23gDTension in the thread for extension of 2mgk in spring is mg
.AThe maximum extension of the spring is 4mgk.BThe speed of A when extension in spring is 2mgk is 2g√2m3k.CThe acceleration of block B when the extension in the spring is maximum, is 23gDTension in the thread for extension of 2mgk in spring is mgIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are 1ms−2 downwards and 5ms−2 downwards, respectively. Acceleration of block 3 relative to 4 is zero.

Find the absolute acceleration of block 1.A2ms−2 upwardsB1ms−2 downwardsC3ms−2 upwardsD1.5ms−2 downwards
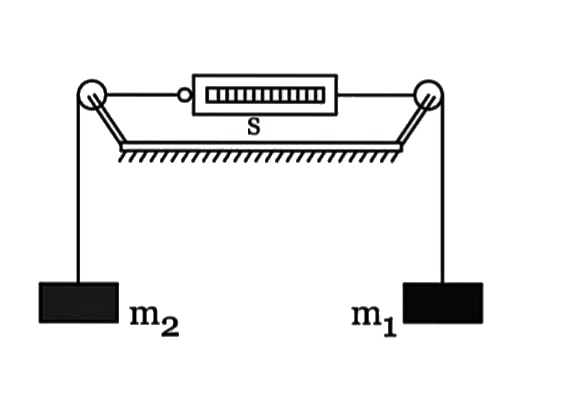
In the arrangement shown, the pulleys, string and the spring balance, all the ideal. If m1>m2, then the reading of the spring balance is
View SolutionIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are 1ms−2 downwards and 5ms−2 downwards, respectively. Acceleration of block 3 relative to 4 is zero.

Find the absoulte acceleration of block 2.
View SolutionIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are 1ms−2 downwards and 5ms−2 downwards, respectively. Acceleration of block 3 relative to 4 is zero.

Find the absoulte acceleration of block 3.
View SolutionIn the arrangement shown in fig., all pulleys are smooth and massless. When the system is released from the rest, acceleration of block 2 and 3 relative to 1 are 1ms−2 downwards and 5ms−2 downwards, respectively. Acceleration of block 3 relative to 4 is zero.

Find the absoulte acceleration of block 4.
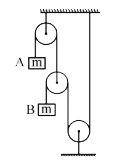
View SolutionIn the arrangement shown, the pulleys and strings are massless. The acceleration of block B is :
View Solution