A tapering rod of length L has cross sectional radii of a and b(<a) at its two ends. Its thermal conductivity is k. The end with radius a is maintained at a higher temperature T1 and the other end is maintained at a lower temperature T2. The curved surface is insulated.
(i) At which of the two points–1 and 2– shown in the figure will the temperature gradient be higher?
(ii) Calculate the thermal resistance of the rod.
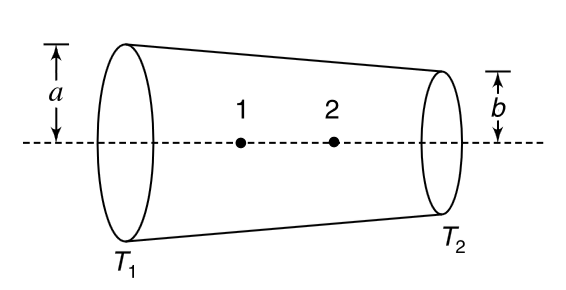
The correct Answer is:(a) At point 2 (ii) Lkπab
Step by step video, text & image solution for A tapering rod of length L has cross sectional radii of a and b(lt a) at its two ends. Its thermal conductivity is k. The end with radius a is maintained at a higher temperature T_(1) and the other end is maintained at a lower temperature T_(2). The curved surface is insulated. (i) At which of the two points – 1 and 2 – shown in the figure will the temperature gradient be higher? (ii) Calculate the thermal resistance of the rod. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The space between two thin concentric metallic spherical shells of radii a and b is filled with a thermal conducting medium of conductivity k. The inner shell is maintained at temperature T1 and outer is maintained at a lower temperatureT2 . Calculate the rate of flow of heat in radially outward direction through the medium.
View SolutionA rod of length l with thermally insulated lateral surface is made of a material whose thermal conductivity varies as K=sc/T where c is a constant. The ends are kept at temperatures T1 and T2. Find the temperature at a distance x from te first end where the temperature is T1 and the heat flow density.
View Solution
Knowledge Check
A slab of material has area A, thickness L, and thermal conducitivy k. One of its surface (P ) is maintained at temperature T1 and the other surface (Q ) is maintained at a lower temperature T2. The rate of heat flow from P to Q is :
AkA(T1−T2)L2BkL(T1−T2)ACkL(T1−T2)LDk(T1−T2)(LA)A rod of length l and cross sectional area A has a variable conductivity given by K=αT, where α is a positive constant T is temperatures in Kelvin. Two ends of the rod are maintained at temperatures T1 and T2(T1>T2). Heat current flowing through the rod will be
AAαT21−T22lBAαT21+T22lCAαT21+T223lDAαT21−T222lA rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
AAα(T21−T22)lBAα(T21+T22)lCAα(T21+T22)3lDAα(T21−T22)2l
A metal rod of length 2 m has cross sectional areas 2 A and A as shown in figure. The ends are maintained at temperatures 100° C and 70° C . The temperature at middle point C is

View SolutionTwo bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is

View SolutionTwo rods of same length and cross section are joined along the length. Thermal conductivities of first and second rod are K1 and K2. The temperature of the free ends of the first and seconds rods are maintained at θ1 and θ2 respectively. The temperature of the common junction is
View Solution
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
View SolutionA rod AB is 1m long. The temperature of its one end A is maintained at 100∘C and other end B at 10∘C, the temperature at a distance of 60 cm from point B is
View Solution

