A rod AB is 1m long. The temperature of its one end A is maintained at C and other end B at C, the temperature at a distance of 60 cm from point B is
C
C
C
C
The correct Answer is:A
To find the temperature at a distance of 60 cm from point B in a rod AB that is 1 meter long, with one end A at 100°C and the other end B at 10°C, we can use the concept of linear temperature distribution in a uniform rod.
1. Identify the Lengths and Temperatures:
- Length of the rod (AB) = 1 m = 100 cm
- Temperature at end A (T_A) = 100°C
- Temperature at end B (T_B) = 10°C
- Distance from point B to point C (where we need to find the temperature) = 60 cm
2. Calculate the Distance from Point A:
- Since the total length of the rod is 100 cm, the distance from point A to point C (T_C) is:
Distance from A to C=Total length−Distance from B to C=100 cm−60 cm=40 cm
3. Use the Formula for Temperature Distribution:
- The temperature at any point in a uniform rod can be calculated using the formula:
T(x)=TA+(TB−TAL)⋅x
- Where:
- T(x) = temperature at distance x from point A
- TA = temperature at point A
- TB = temperature at point B
- L = total length of the rod
- x = distance from point A
4. Substitute the Values:
- Here, TA=100°C, TB=10°C, L=100 cm, and x=40 cm:
T(40)=100+(10−100100)⋅40
T(40)=100+(−90100)⋅40
T(40)=100−36=64°C
5. Conclusion:
- The temperature at a distance of 60 cm from point B (or 40 cm from point A) is 64°C.
- Length of the rod (AB) = 1 m = 100 cm
- Temperature at end A (T_A) = 100°C
- Temperature at end B (T_B) = 10°C
- Distance from point B to point C (where we need to find the temperature) = 60 cm
- Since the total length of the rod is 100 cm, the distance from point A to point C (T_C) is:
Distance from A to C=Total length−Distance from B to C=100 cm−60 cm=40 cm
- The temperature at any point in a uniform rod can be calculated using the formula:
T(x)=TA+(TB−TAL)⋅x
- Where:
- T(x) = temperature at distance x from point A
- TA = temperature at point A
- TB = temperature at point B
- L = total length of the rod
- x = distance from point A
- Here, TA=100°C, TB=10°C, L=100 cm, and x=40 cm:
T(40)=100+(10−100100)⋅40
T(40)=100+(−90100)⋅40
T(40)=100−36=64°C
- The temperature at a distance of 60 cm from point B (or 40 cm from point A) is 64°C.
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY AND HEAT TRANSFERExercise:Match the columns
Explore 4 Videos
- CALORIMETRY & HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY & HEAT TRANSFERExercise:Level 2 Subjective
Explore 14 Videos
- CENTRE OF MASSBook:DC PANDEYChapter:CENTRE OF MASSExercise:Medical entrances gallery
Explore 27 Videos
Similar Questions
Two rods of material, x and two of y are connected as shown in the figure. All the rods are indentical in length and cross-sectional area. If the end A is maintained at 80∘C and the end D is maintained at 10∘C, calculate the temperature of the junctions B and C in the steady state. Thermal conductivity of x is double that of y.

View SolutionFew rods of material X and Y are connected as shown in figure - 4.10. The cross sectional area of all the rods are same. If the end A is maintained at 80∘C and the end F is maintained at 10^(@)C~ . Calculate the temperatures of junctions B and E in steady state . Given that thermal conductivty of material X is double that of Y.
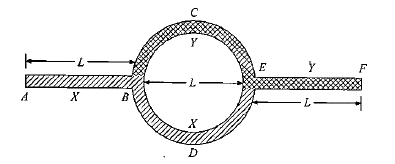
View Solution
Knowledge Check
The end A of rod AB of length 1 m is maintained at 80∘C and the end B at 0∘C. The temperature at a distance of 60 cm from the end A is
A16∘CB32∘CC48∘CD64∘CIn a steady state of heat conduction the temperature of the ends A and B of a rod 100cm long per 0∘C and 100∘C The temperature of the rod at a point 60cm distant from the end A is .
A0∘CB40∘CC60∘CD100∘CA cylindrical steel rod of length 0.10 m and thermal conductivity 50W.m−1K−1 is welded end to end to copper rod of thermal conductivity 400W.m−1.K−1 and of the same area of cross section but 0.20 m long. The free end of the steel rod is maintained at 100∘C and that of the copper and at 0∘C. Assuming that the rods are perfectly insulated from the surrounding, the temperature at the junction of the two rods–
A20∘CB30∘CC40∘CD50∘C
Three identical rods have been joined at a junction to make it a Y shape structure .If two free ends are maintained at 60∘C and the thired end is at 0∘C then what is the juction temperature θ?
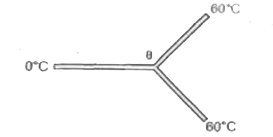
View SolutionThe temperature of hot and cold end of a 20 cm long rod in thermal steady state are at 100∘C and 20∘C respectively. Temperature at the centre of the rod is
View SolutionSeven identical rods of matrical of thermal conductivity k are connected as shown in All the rod are of identical length l and cross sectional area A if the one end b is kept at 100∘C and the other end is kept at 0∘C The temperatures of the junctions C,D and E(θDandθE) be in the steady state
 .
.
View SolutionIn the steady state the two ends of a meter rod are at 30∘C and 20∘C the temperature at the 40thcm from the end at higher temperature is .
View SolutionA rod of negligible heat capacity has a length of 50 cm, area of cross section 5cm2 and thermal conductivity 500 W/m∘C. The temperature of one end is maintained at 0∘C and that fo the other end is slowly and linearly varied from 0∘C to 60∘C in 20 min. Assuming no heat loss through the lateral side, the total heat transmitted throught he rod in 20 minutes is
View Solution

