The temperature of hot and cold end of a 20 cm long rod in thermal steady state are at 100∘C and 20∘C respectively. Temperature at the centre of the rod is
50∘C
60∘C
40∘C
30∘C
The correct Answer is:B
To find the temperature at the center of a 20 cm long rod in thermal steady state with hot and cold ends at 100°C and 20°C respectively, we can follow these steps:
1. Identify the Given Information:
- Length of the rod (L) = 20 cm
- Temperature at the hot end (T_hot) = 100°C
- Temperature at the cold end (T_cold) = 20°C
2. Understand the Concept of Thermal Steady State:
- In thermal steady state, the temperature gradient along the rod is linear. This means that the temperature changes uniformly from the hot end to the cold end.
3. Determine the Temperature at the Center of the Rod:
- The center of the rod is located at half the length of the rod. Therefore, the center position (x) is:
x=L2=20cm2=10cm
- The temperature at any point in a uniformly varying temperature gradient can be calculated using the formula:
T(x)=Tcold+(Thot−TcoldL)⋅x
- Substituting the known values into the equation:
T(10cm)=20°C+(100°C−20°C20cm)⋅10cm
4. Calculate the Temperature Gradient:
- The temperature difference between the hot and cold ends is:
Thot−Tcold=100°C−20°C=80°C
- The temperature gradient (slope) is:
80°C20cm=4°C/cm
5. Calculate the Temperature at the Center:
- Now, substituting the gradient back into the temperature equation:
T(10cm)=20°C+(4°C/cm)⋅10cm=20°C+40°C=60°C
6. Final Result:
- The temperature at the center of the rod is:
T(10cm)=60°C
Summary:
The temperature at the center of the rod is 60°C.
- Length of the rod (L) = 20 cm
- Temperature at the hot end (T_hot) = 100°C
- Temperature at the cold end (T_cold) = 20°C
- In thermal steady state, the temperature gradient along the rod is linear. This means that the temperature changes uniformly from the hot end to the cold end.
- The center of the rod is located at half the length of the rod. Therefore, the center position (x) is:
x=L2=20cm2=10cm
- The temperature at any point in a uniformly varying temperature gradient can be calculated using the formula:
T(x)=Tcold+(Thot−TcoldL)⋅x
- Substituting the known values into the equation:
T(10cm)=20°C+(100°C−20°C20cm)⋅10cm
- The temperature difference between the hot and cold ends is:
Thot−Tcold=100°C−20°C=80°C
- The temperature gradient (slope) is:
80°C20cm=4°C/cm
- Now, substituting the gradient back into the temperature equation:
T(10cm)=20°C+(4°C/cm)⋅10cm=20°C+40°C=60°C
- The temperature at the center of the rod is:
T(10cm)=60°C
The temperature at the center of the rod is 60°C.
Topper's Solved these Questions
- TRANSMISSION OF HEATBOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - Convection
13 Videos
- TRANSMISSION OF HEATBOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - Radiation (General, Kirchoff s law, Black body)
38 Videos
- THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY BOOK - ERRORLESS CHAPTER - THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY EXERCISE - Self Evaluation Test
15 Videos
- UNITS, DIMENSION & MEASUREMENTSBOOK - ERRORLESS CHAPTER - UNITS, DIMENSION & MEASUREMENTSEXERCISE - All Questions
333 Videos
Similar Questions
A wall consists of two layer, one of thickness 3 cm and other of 6 cm. the thermal conductivities of the materials of these layers are K and 3K respectively. The temperature of the outer surfaces of the two layers are −5∘C and 20∘C respectively. determine the temperature of the surface of contact of the two layers in the steady state.
View SolutionThe temperature of the two ends A and B of a rod of length 25cm and circular cross section are 100∘C and 0∘C respectively In the steady state, find the temperature at a point 10cm from the end B (ifnore loss of heat from curved surface of the body) ?
View Solution
Knowledge Check
Temperature of hot end and cold end of a rod, which is in steady state are 100∘C and 40∘C respectively. The area of cross section of rod and its thermal conductivity are uniform. The temperature of rod at its mid point is (Assume no heat loss thorugh lateral surface)
A70∘CB60∘CC80∘CDNone of theseIn a steady state of thermal conduction, temperature of the ends A and B of a 20 cm long rod are 100∘C and 0∘C respectively. What will be the temperature of the rod at a point at a distance of 6 cm from the end A of the rod
A−30∘CB70∘CC5∘CDNone of the aboveTwo ends of a conducting rod of varying cross-section are maintained at 200∘Cand0∘C respectively. In steady state :
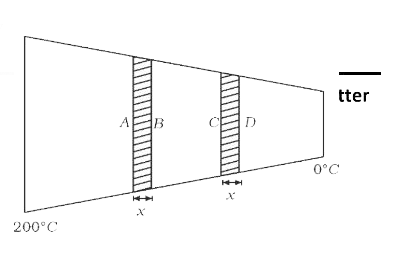 Atemperature differences across AB and CD are equalBtemperature difference across AB is greater than that across CDCtemperature difference across AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Atemperature differences across AB and CD are equalBtemperature difference across AB is greater than that across CDCtemperature difference across AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Rods X and Y of identical dimensions but of different materials are joined as shown in The length of each part is the same It the temperature of end A and F be main tained at 100∘C and 20∘C respectively then find the temperatures of the junctions B and E (Thermal conductivity of X is double that of Y) .
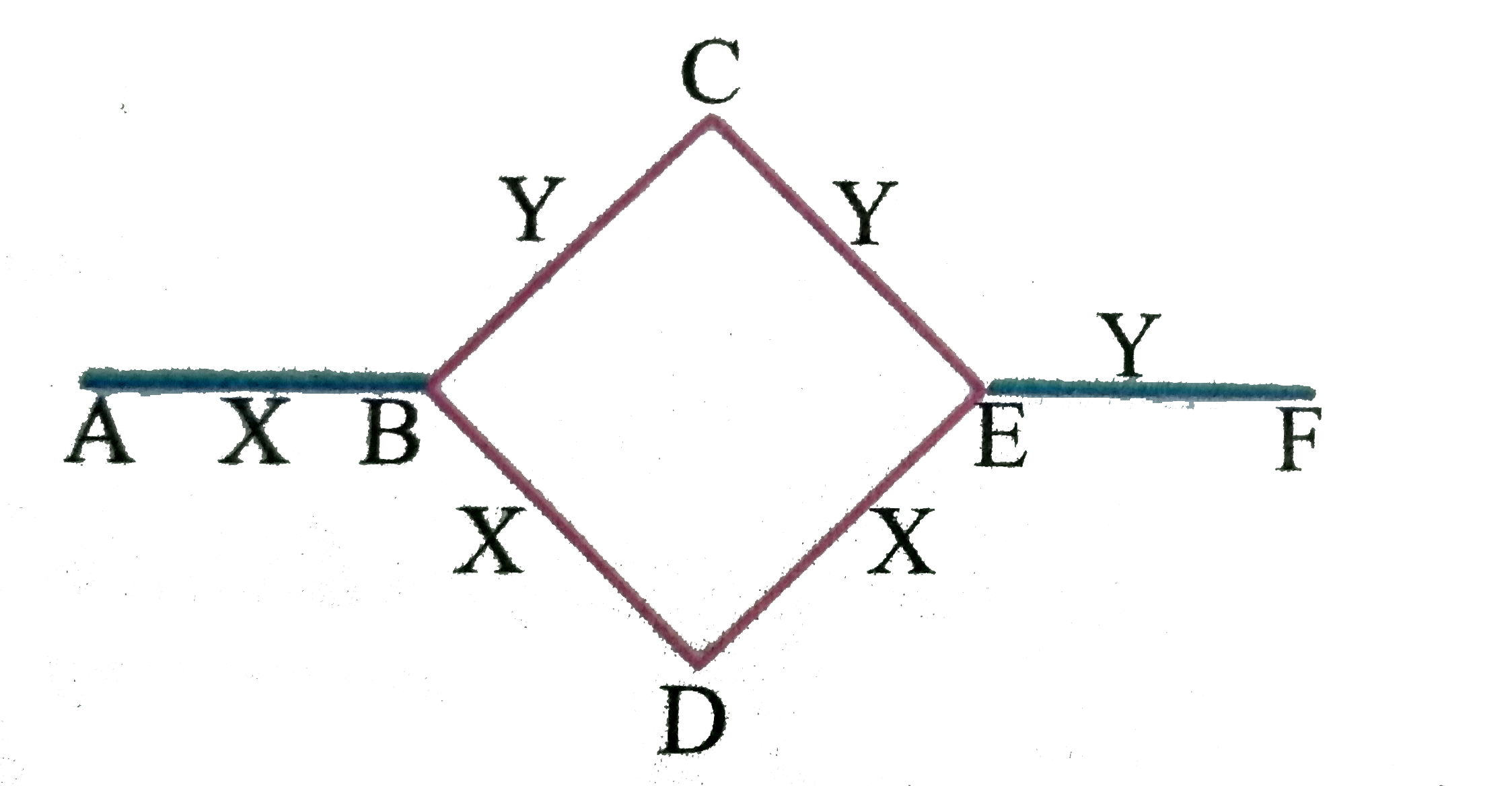
View SolutionTwo rods of same dimensions, but made of different materials are joined end to end to end with their free end being maintained at 100∘C and 0∘C respectively. The temperature of the junction is 70∘C. Then the temperature of the junction if the rods are inerchanged will be equal to T∘C Find T:
View SolutionTwo ends of a conducting rod of varying cross-section are maintained at 200∘C and 0∘C respectively. In steady state:

View SolutionIn the steady state the two ends of a meter rod are at 30∘C and 20∘C the temperature at the 40thcm from the end at higher temperature is .
View SolutionTwelve conducting rods from the sides of a uniform cube of side l. If in steady state, B and H ends of the cube are at 100∘C and 0∘C respectively. Find the temperature of the junction 'A' :-
_E01_117_Q01.png)
View Solution
