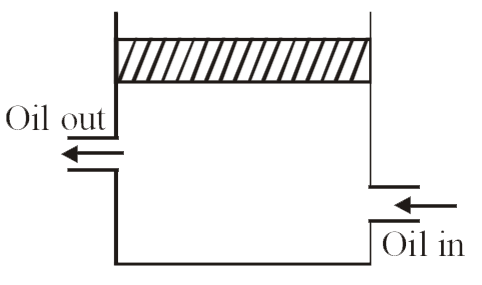
The top of an insulated cylindrical container is covered by a disc having emissivity 0.6 and conductivity 0.167 WK–1m–1 and thickness 1 cm. The temperature is maintained by circulating oil as shown in figure. Find the radiation loss to the surrounding in Jm–2s–1if temperature of the upper surface of the disc is 127∘C and temperature of the surrounding is 27∘C.
595J/m×sec
595cal/m×sec
991.0J/m×sec
440J/m×sec
The correct Answer is:D
Step by step video, text & image solution for The top of an insulated cylindrical container is covered by a disc having emissivity 0.6 and conductivity 0.167 "WK"^(– 1)m^(–1) and thickness 1 cm. The temperature is maintained by circulating oil as shown in figure. Find the radiation loss to the surrounding in "Jm"^(–2)s^(–1 )if temperature of the upper surface of the disc is 127^(@)"C" and temperature of the surrounding is 27^(@)"C". by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRANSMISSION OF HEATBOOK - ERRORLESS CHAPTER - TRANSMISSION OF HEATEXERCISE - Assertion & Reason
24 Videos
- THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY BOOK - ERRORLESS CHAPTER - THERMOMETRY, THERMAL EXPANSION AND CALORIMETRY EXERCISE - Self Evaluation Test
15 Videos
- UNITS, DIMENSION & MEASUREMENTSBOOK - ERRORLESS CHAPTER - UNITS, DIMENSION & MEASUREMENTSEXERCISE - All Questions
333 Videos
Similar Questions
A heated iron block at 127 ∘C loses "300J of heat to the surrounding which is at a temperature of 27∘C.Delta S for this process is 0.05xJK^(-1) Find the value of x.
View SolutionSix identical conducting rods are connected as shown in figure. In steady state temperature of point ϕ1 is fixed at 100∘C and temperature of ϕ6 at −80∘C

Q. What is the temperature of ϕ2?
View Solution
Knowledge Check
If two conducting slabs of thickness d1 and d2, and thermal conductivity K1 and K2 are placed together face to face as shown in figure in the steady state temperature of outer surfaces are θ1 and θ2. The temperature of common surface is-
 AK1θ1d1+K2θ2d2K1d1+K2d2BK1θ1+K2θ2K1+K2CK1θ1+K2θ2θ1+θ2DK1θ1d2+K2θ2d1K1d2+K2d1
AK1θ1d1+K2θ2d2K1d1+K2d2BK1θ1+K2θ2K1+K2CK1θ1+K2θ2θ1+θ2DK1θ1d2+K2θ2d1K1d2+K2d12 litres water at 27∘C is heated by a 1kW heater in an open container. On an average heat is lost to surroundings at the rate 160J/s. The time required for the temperature to reach 77∘C is
A8min20secB10minC7minD14minIf two conducting slabs of thickness d1 and d2, and thermal conductivity K1 and K2 are placed together face to face as shown in figure in the steady state temperature of outer surfaces are θ1 and θ2. The temperature of common surface is-
 AK1θ1d1+K2θ2d2K1d1+K2d2BK1θ1+K2θ2K1+K2CK1θ1+K2θ2θ1+θ2DK1θ1d2+K2θ2d1K1d2+K2d1
AK1θ1d1+K2θ2d2K1d1+K2d2BK1θ1+K2θ2K1+K2CK1θ1+K2θ2θ1+θ2DK1θ1d2+K2θ2d1K1d2+K2d1
Six identical conducting rods are connected as shown in figure. In steady state temperature of point ϕ1 is fixed at 100∘C and temperature of ϕ6 at −80∘C

Q. What is the temperature of ϕ3?
View SolutionSix identical conducting rods are connected as shown in figure. In steady state temperature of point ϕ1 is fixed at 100∘C and temperature of ϕ6 at −80∘C
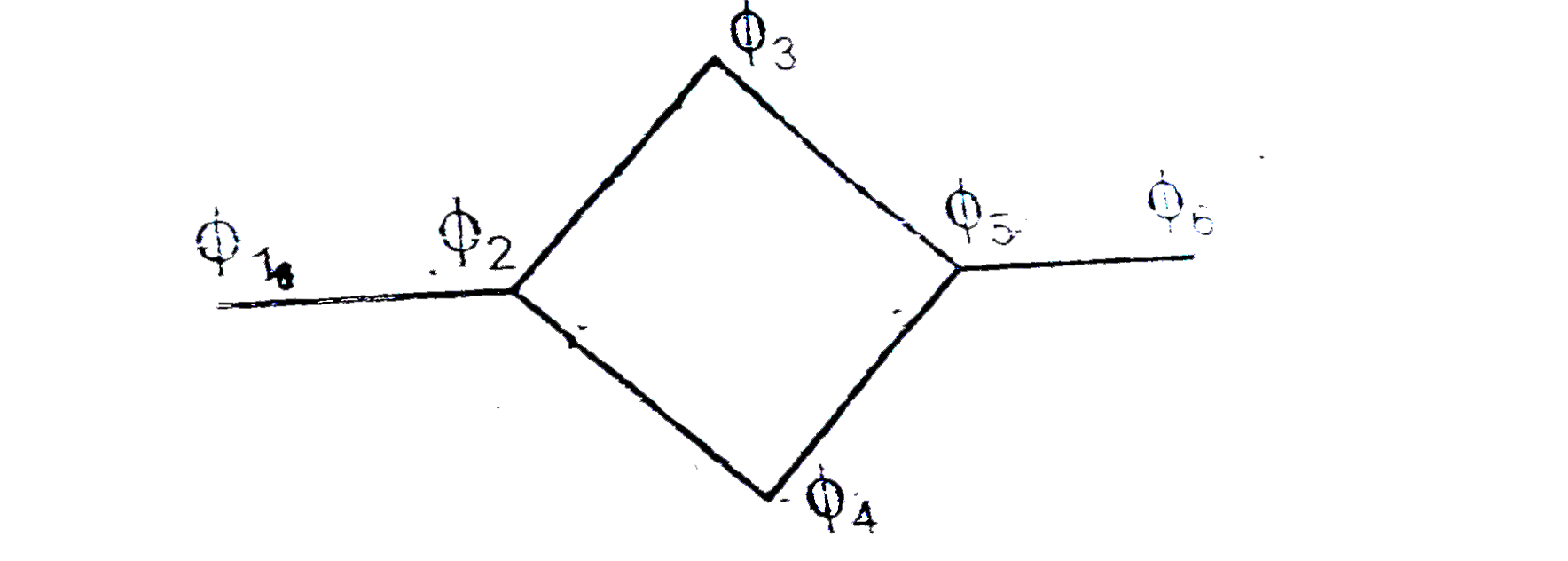
Q. What is the temperature of ϕ5?
View SolutionAn insulated container has a wooden lid at the top whose conductivity is 0.15J/m∘Cs , thickness is 5 mm and emissivity is 0.5. The temperature of the top of the wooden lid is maintained at 125∘C and the ambient temperature is 27∘C . Hot liquid is now circulated through the container as shown in the figure. Determine the rate of loss of heat per unit area due to radiation from the wooden lid and temperature of the oil.

Take σ=5.66×10−8Wm−2K−4
View SolutionA heated irron block at 127∘C loses 300J of heat to the surroundings which are at a temperature of 27∘C. This process is 0.05JK−1. Find the value of x.
View SolutionStatement-1: If the temperature of body and surrounding is same then no heat is radiated by the body.
Statement-2: The rise of 1∘C is equivalent to 1.8∘F
Statement-3: If heat is given to the system then temperature of the system must rise.
View Solution
