A wall consists of two layer, one of thickness 3 cm and other of 6 cm. the thermal conductivities of the materials of these layers are K and 3K respectively. The temperature of the outer surfaces of the two layers are −5∘C and 20∘C respectively. determine the temperature of the surface of contact of the two layers in the steady state.
The correct Answer is:10∘C
To determine the temperature at the surface of contact of the two layers in the steady state, we can follow these steps:
Step 1: Understand the setup
We have two layers of a wall:
- Layer A: Thickness = 3 cm, Thermal conductivity = K
- Layer B: Thickness = 6 cm, Thermal conductivity = 3K
- Outer surface temperatures: T1 = -5°C (for Layer A) and T2 = 20°C (for Layer B)
Step 2: Set up the heat flow equation
In steady state, the rate of heat flow through both layers must be equal. We denote the temperature at the interface of the two layers as T.
The heat flow through Layer A (dQ/dt)_A can be expressed as:
dQdt=K⋅A⋅(T−T1)LA
Where:
- T1=−5°C
- LA=3 cm=0.03 m
The heat flow through Layer B (dQ/dt)_B can be expressed as:
dQdt=3K⋅A⋅(T2−T)LB
Where:
- T2=20°C
- LB=6 cm=0.06 m
Step 3: Equate the heat flows
Since the heat flow is the same through both layers, we can set the two equations equal to each other:
K⋅A⋅(T−(−5))0.03=3K⋅A⋅(20−T)0.06
Step 4: Simplify the equation
We can cancel K and A from both sides, as they are common factors:
T+50.03=3(20−T)0.06
Next, simplify the right side:
T+50.03=3⋅20−3T0.06
T+50.03=60−3T0.06
Multiply both sides by 0.06 to eliminate the denominators:
2(T+5)=60−3T
Step 5: Solve for T
Expanding the left side:
2T+10=60−3T
Rearranging gives:
2T+3T=60−10
5T=50
T=10°C
Conclusion
The temperature at the surface of contact of the two layers in the steady state is 10°C.
---
We have two layers of a wall:
- Layer A: Thickness = 3 cm, Thermal conductivity = K
- Layer B: Thickness = 6 cm, Thermal conductivity = 3K
- Outer surface temperatures: T1 = -5°C (for Layer A) and T2 = 20°C (for Layer B)
In steady state, the rate of heat flow through both layers must be equal. We denote the temperature at the interface of the two layers as T.
dQdt=K⋅A⋅(T−T1)LA
Where:
- T1=−5°C
- LA=3 cm=0.03 m
dQdt=3K⋅A⋅(T2−T)LB
Where:
- T2=20°C
- LB=6 cm=0.06 m
Since the heat flow is the same through both layers, we can set the two equations equal to each other:
K⋅A⋅(T−(−5))0.03=3K⋅A⋅(20−T)0.06
We can cancel K and A from both sides, as they are common factors:
T+50.03=3(20−T)0.06
T+50.03=3⋅20−3T0.06
T+50.03=60−3T0.06
2(T+5)=60−3T
Expanding the left side:
2T+10=60−3T
2T+3T=60−10
5T=50
T=10°C
The temperature at the surface of contact of the two layers in the steady state is 10°C.
Topper's Solved these Questions
- THERMODYNAMICSBook:SL ARORAChapter:THERMODYNAMICSExercise:Exercise
Explore 342 Videos
- THERMODYNAMICSBook:SL ARORAChapter:THERMODYNAMICSExercise:Problems from competitive examinations
Explore 22 Videos
- Thermal Properties of MatterBook:SL ARORAChapter:Thermal Properties of MatterExercise:Exercise
Explore 449 Videos
- Units and MeasurementsBook:SL ARORAChapter:Units and MeasurementsExercise:Exercise
Explore 499 Videos
Similar Questions
A composite wall of area A is made of equal thickness of lead and iron having thermal conductivities K and 2K, respectively. The temperature on the two sides of the composite wall are 100∘C and 0∘C with the layer on the hotter side. Calculate the steady -state temperature of the lead-iron interface.
View SolutionTwo walls of thickness in the ratio 1:3 and thermal conductivities in the ratio 3:2 form a composite wall of a building. If the free surfaces of the wall be at temperatures 30∘C and 20∘C, respectively, what is the temperature of the interface?
View Solution
Knowledge Check
The temperature of hot and cold end of a 20 cm long rod in thermal steady state are at 100∘C and 20∘C respectively. Temperature at the centre of the rod is
A50∘CB60∘CC40∘CD30∘CIn a steady state of thermal conduction, temperature of the ends A and B of a 20 cm long rod are 100∘C and 0∘C respectively. What will be the temperature of the rod at a point at a distance of 6 cm from the end A of the rod
A−30∘CB70∘CC5∘CDNone of the aboveA composite slab consists of two parts of equal thickness. The thermal conductivity of one is twice that of the other. What will be the ratio of temperature difference across the two layers in the state of equilibrium ?
A1B2C3D4
Three identical rods are joined in series as shown. Their thermal conductivities are K,K/2 and K/3 respectively. At steady, if the free ends of rods are at 100∘C and 20∘C respectively. Determine the temperature at two junction points. Also find the equivalent thermal conductivity.
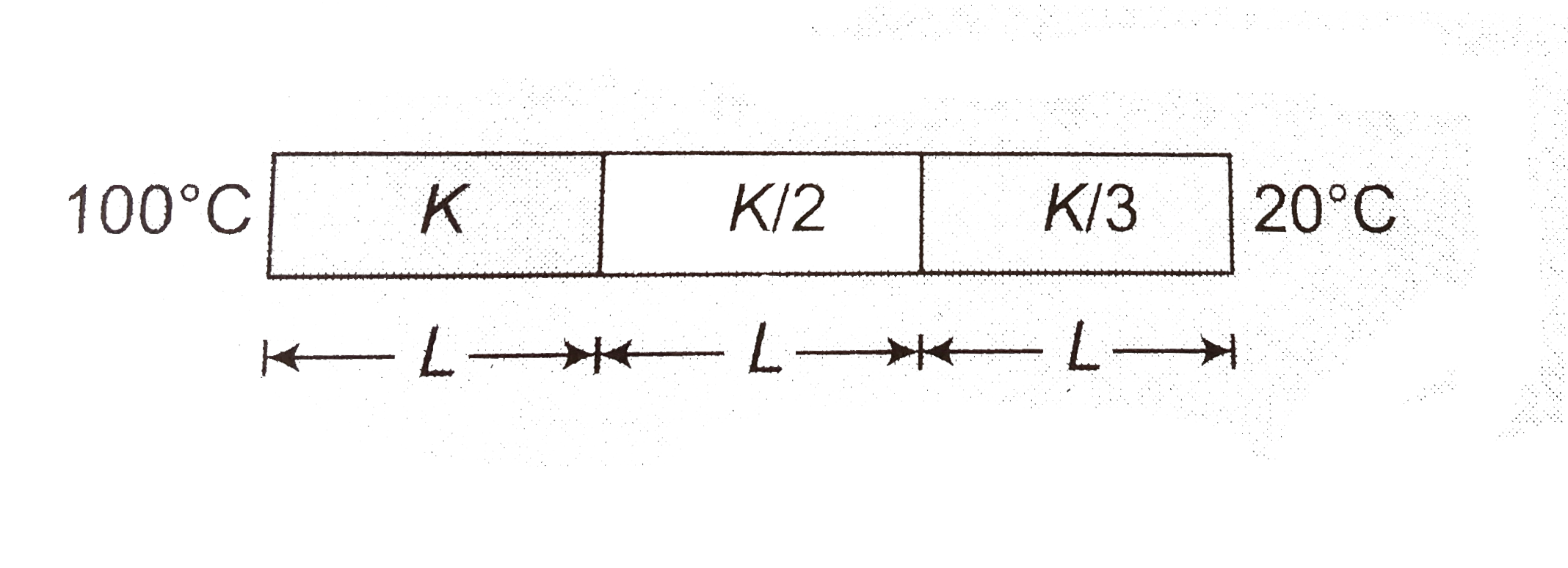
View SolutionHeat is conducted through a slab composed of paralel layers of two different materials of conductivities 134.4 SI units and 58.8 SI units and of thickness 3.6cm and 4.2cm respectively. The temperature of the outer faces of the compound slab are 96∘C and 8∘C. Find (i) the temperature of the interface, (ii) temperature gradient in each section of the slab.
View SolutionA slab consists of two parallel layers of different materials 4cm and 2cm thick and of thermal conductivities 54cals−1m−1K−1 and 36cals−1m−1K−1 respectively. If the faces of the slab are at 100∘C and 0∘C calculate the temperature of the surface dividing the two materials.
View SolutionIf layer thickness L2 is 1.4cm, then its thermal conductivity K2 will have value (in W/mK)
View SolutionTemperature of water at the surface of lake is −20∘C. Then temperature of water just below the lower surface of ice layer is
View Solution

