The thermal conductivity of copper is four times that of brass. Two rods of copper and brass of same length and cross-section are joined end to end. The free end of copper rod is at 0∘C and that of brass rod at 100∘C. Calculate the temperature of junction at equilibrium. neglect radiation losses.
The correct Answer is:20∘C
To solve the problem of finding the temperature at the junction of two rods (copper and brass) joined end to end, we can follow these steps:
1. Identify Given Data:
- Let the thermal conductivity of brass be k.
- Therefore, the thermal conductivity of copper is 4k (as given).
- Both rods have the same length L and cross-sectional area A.
- The temperature at the free end of the copper rod is 0∘C and at the free end of the brass rod is 100∘C.
2. Define the Temperature at the Junction:
- Let the temperature at the junction be T.
3. Apply the Heat Flow Equation:
- The rate of heat flow through the copper rod can be expressed as:
dQdt=kCu⋅AL(T−0)=4k⋅ALT
- The rate of heat flow through the brass rod can be expressed as:
dQdt=kBr⋅AL(100−T)=k⋅AL(100−T)
4. Set the Heat Flow Rates Equal:
- Since the system is in equilibrium, the rate of heat flow through both rods must be equal:
4k⋅ALT=k⋅AL(100−T)
5. Cancel Common Terms:
- We can cancel k, A, and L from both sides:
4T=100−T
6. Solve for T:
- Rearranging the equation gives:
4T+T=100
5T=100
T=1005=20∘C
7. Conclusion:
- The temperature at the junction at equilibrium is T=20∘C.
- Let the thermal conductivity of brass be k.
- Therefore, the thermal conductivity of copper is 4k (as given).
- Both rods have the same length L and cross-sectional area A.
- The temperature at the free end of the copper rod is 0∘C and at the free end of the brass rod is 100∘C.
- Let the temperature at the junction be T.
- The rate of heat flow through the copper rod can be expressed as:
dQdt=kCu⋅AL(T−0)=4k⋅ALT
- The rate of heat flow through the brass rod can be expressed as:
dQdt=kBr⋅AL(100−T)=k⋅AL(100−T)
- Since the system is in equilibrium, the rate of heat flow through both rods must be equal:
4k⋅ALT=k⋅AL(100−T)
- We can cancel k, A, and L from both sides:
4T=100−T
- Rearranging the equation gives:
4T+T=100
5T=100
T=1005=20∘C
- The temperature at the junction at equilibrium is T=20∘C.
Topper's Solved these Questions
- THERMODYNAMICSBook:SL ARORAChapter:THERMODYNAMICSExercise:Exercise
Explore 342 Videos
- THERMODYNAMICSBook:SL ARORAChapter:THERMODYNAMICSExercise:Problems from competitive examinations
Explore 22 Videos
- Thermal Properties of MatterBook:SL ARORAChapter:Thermal Properties of MatterExercise:Exercise
Explore 449 Videos
- Units and MeasurementsBook:SL ARORAChapter:Units and MeasurementsExercise:Exercise
Explore 499 Videos
Similar Questions
Figure shows a copper rod joined to a steel rod. The rods have equal length and and the equal cross sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C . Find the temperature at the junction of the rods. conductivity of copper =390WM−1^(@)C^(-1)andtˆofsteel=46Wm^(-1)(∘)C−1 .

View SolutionTwo rods having thermal conductivity in the ratio of 5 : 3 having equal lengths and equal cross-sectional area are joined by face to face. If the temperature of the free end of the first rod is 100∘C and free end of the second rod is 20∘C . Then temperature of the junction is
View Solution
Knowledge Check
Two rods of copper and brass having the same length and cross - section are joined end to end. The free end of the copper is at 0∘C and of brass is at 80∘C in steady-state. If thermal conductivity of copper is 4 times of that of brass find the temp. at junction of two rods
A80∘CB64∘CC20∘CD16∘CA large cylindrical rod of length L is made by joining two identical rods of copper and steel of length (L2) each. The rods are completely insulated from the surroundings. If the free end of copper rod is maintained at 100∘C and that of steel at 0∘C then the temperature of junction is (Thermal conductivity of copper is 9 times that of steel)
A90∘CB50∘CC10∘CD67∘CA slab consists of two parallel layers of copper and brass of the same thichness and having thermal conductivities in the ratio 1:4 If the free face of brass is at 100∘C anf that of copper at 0∘C the temperature of interface is .
A80∘CB20∘CC60∘CD40∘C
A metallic prong consists of 4 rods made of the same material, cross-section and same lengths as shown. The three forked ends are kept at 100∘C and the handle end is at 0∘C. The temperature of the junction is
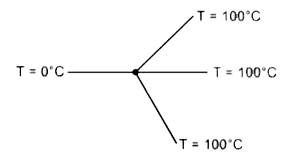
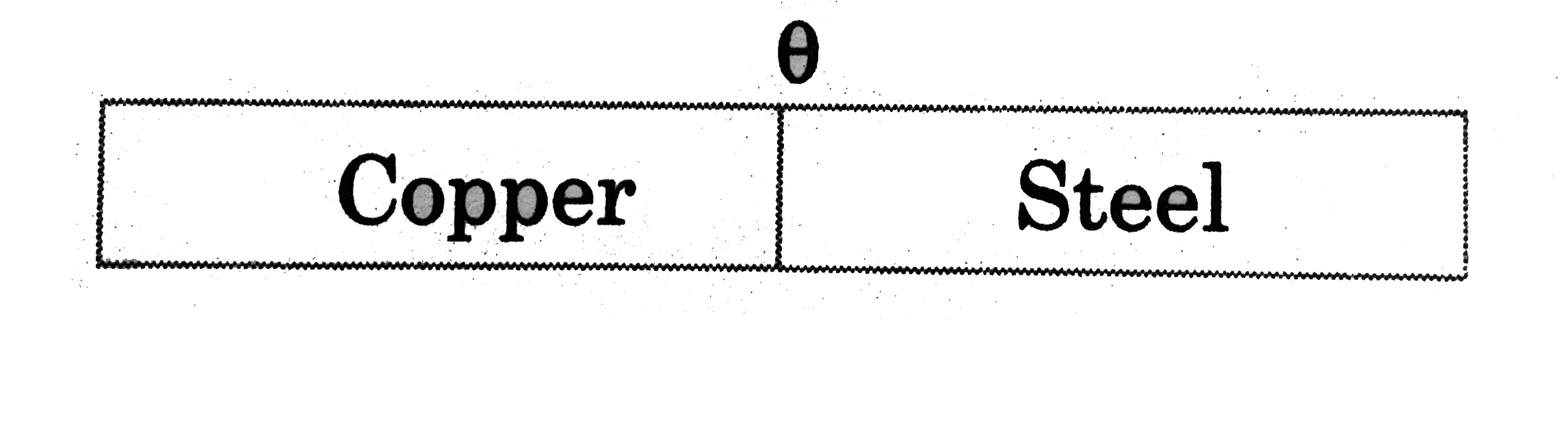
View SolutionFigure shows a copper rod joined to a steel rod. The rods have equal length and equal cross-sectional area. The free end of the copper rod is kept at 0∘C and that of the steel rod is kept at 100∘C. Find the temperature θ at the junction of the rods. Conductivity of copper
=390W/m−∘C and that of steel =46W/m−∘C.
 .
.
View SolutionA slab consists of two parallel layers of copper and brass of the time thickness and having thermal conductivities in the ratio 1:4. If the free face of brass is at 35∘C and that of copper at 1:√2.5, the temperature of interface is
View SolutionTwo rods of different materials having differnet lengths and same cross sectional areas are joined end to end in a straight line. The free ends of this compound rod are maintained at different temperatures The temperature gradient in each rod will be .
View SolutionA compound slab is made of two parallel plates of copper and brass of the same thickness and having thermal conductivities in the ratio 4:1. The free face of copper is at 0∘C. The temperature of the internal is 20∘C. What is the temperature of the free face of brass?
View Solution

