Temperature of hot end and cold end of a rod, which is in steady state are 100∘C and 40∘C respectively. The area of cross section of rod and its thermal conductivity are uniform. The temperature of rod at its mid point is (Assume no heat loss thorugh lateral surface)
70∘C
60∘C
80∘C
None of these
The correct Answer is:A
To find the temperature at the midpoint of the rod, we can use the concept of steady-state heat conduction. Here’s the step-by-step solution:
Step 1: Understand the Setup
We have a rod with two ends at different temperatures:
- Hot end (Point P): T1=100∘C
- Cold end (Point Q): T2=40∘C
The rod is in steady state, meaning the temperature distribution along the rod does not change with time.
Step 2: Identify the Midpoint
Let’s denote the midpoint of the rod as Point C. We need to find the temperature at this point, TC.
Step 3: Apply the Concept of Steady-State Heat Conduction
In steady state, the rate of heat transfer through the rod is constant. The heat transfer can be expressed using Fourier's law of heat conduction:
Q=k⋅A⋅(T1−T2)L
Where:
- Q is the rate of heat transfer,
- k is the thermal conductivity,
- A is the cross-sectional area,
- L is the length of the rod.
Step 4: Set Up the Equation for the Midpoint
Since the rod is uniform, we can assume that the temperature gradient is linear between the two ends. Therefore, the temperature at the midpoint can be calculated using the formula:
TC=T1+T22
Step 5: Substitute the Values
Substituting the given temperatures:
TC=100∘C+40∘C2=140∘C2=70∘C
Conclusion
The temperature at the midpoint of the rod is:
70∘C
We have a rod with two ends at different temperatures:
- Hot end (Point P): T1=100∘C
- Cold end (Point Q): T2=40∘C
Let’s denote the midpoint of the rod as Point C. We need to find the temperature at this point, TC.
In steady state, the rate of heat transfer through the rod is constant. The heat transfer can be expressed using Fourier's law of heat conduction:
Q=k⋅A⋅(T1−T2)L
Where:
- Q is the rate of heat transfer,
- k is the thermal conductivity,
- A is the cross-sectional area,
- L is the length of the rod.
Since the rod is uniform, we can assume that the temperature gradient is linear between the two ends. Therefore, the temperature at the midpoint can be calculated using the formula:
TC=T1+T22
Substituting the given temperatures:
TC=100∘C+40∘C2=140∘C2=70∘C
The temperature at the midpoint of the rod is:
70∘C
Topper's Solved these Questions
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) (LEVEL-I) (ASSERTION AND REASON)
Explore 2 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:ASSIGNMENT PROBLEMS (OBJECTIVE) (LEVEL II)
Explore 20 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) (LEVEL II AND III)
Explore 15 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 5 Videos
Similar Questions
Two rods of same length and same material having area of cross section A and 4A respectively are joined as shown in the figure. If TA and TB are temperatures of free ends in steady state. The temperature of junction point C is (Assume no heat loss wil take place through lateral surface)

View SolutionThe temperature of the two ends A and B of a rod of length 25cm and circular cross section are 100∘C and 0∘C respectively In the steady state, find the temperature at a point 10cm from the end B (ifnore loss of heat from curved surface of the body) ?
View Solution
Knowledge Check
The temperature of hot and cold end of a 20 cm long rod in thermal steady state are at 100∘C and 20∘C respectively. Temperature at the centre of the rod is
A50∘CB60∘CC40∘CD30∘CTwo ends of a conducting rod of varying cross-section are maintained at 200∘Cand0∘C respectively. In steady state :
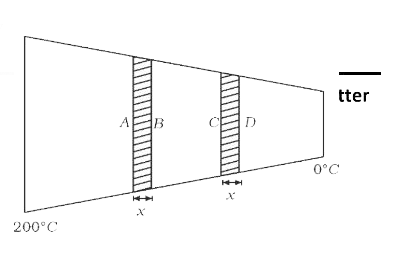 Atemperature differences across AB and CD are equalBtemperature difference across AB is greater than that across CDCtemperature difference across AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Atemperature differences across AB and CD are equalBtemperature difference across AB is greater than that across CDCtemperature difference across AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.Two ends of a conducting rod of varying cross-section are maintained at 200∘C and 0∘C respectively. In steady state:
 Atemperature differences across ABandCD are equalBtemperature difference aross AB is greater than that across CDCtemperature difference aross AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Atemperature differences across ABandCD are equalBtemperature difference aross AB is greater than that across CDCtemperature difference aross AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
One end of a rod of length 20 cm is maintained at 800 K. The temperature of the other end of the rod is 750 K in steady state and this end is blackened to radiate thermal radiations like a black body. If temperature of the surrounding is 300 K, find the thermal conductivity of the rod. Assume no energy loss takes place through the lateral surface of the rod during conduction through its length.
View SolutionCylinder copper rod of length 1m and a cylinder steel rod of length 1.5m are joined together end to end. The cross sectional area of eac rod is 3.14cm. The free ends of steel rod and copper rods are maintained at 0∘C and 100∘C respectively. The surfaces of rods are thermally insulated. Find the temperature of copper steel junction. (Given thermal conductivity of steel =46J/m−s.∘C and the thermal conductivity of copper =386J/m−s.∘C)
View SolutionThe ends of a rod of uniform thermal conductivity are maintained at different (constant) temperatures. Afer the steady state is achieved:
View SolutionA conducting cylindrical rod of uniform cross-sectional area is kept between two large chambers which are at temperatures 100∘C and 0∘C, respectively. The cconductivety of the rod increases with x, where x is distance from 100∘C end. The temperature profile of the rod in steady -state will be as

View SolutionTwo rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
View Solution

