In the steady state the two ends of a meter rod are at 30∘C and 20∘C the temperature at the 40thcm from the end at higher temperature is .
22∘C
26∘C
25∘C
24∘C
The correct Answer is:B
To solve the problem step by step, we will use the concept of linear temperature distribution in a rod that is in steady state.
Step 1: Understand the Setup
We have a meter rod (100 cm) with one end at a temperature of 30∘C and the other end at 20∘C. We need to find the temperature at the 40th cm from the end that is at 30∘C.
Step 2: Identify the Lengths
- The length of the rod is 100cm.
- The distance from the higher temperature end (30°C) to the point of interest (40 cm) is 40cm.
Step 3: Set Up the Linear Temperature Distribution Equation
In steady state, the temperature T at a distance x from the higher temperature end can be expressed as:
T(x)=T1+(T2−T1L)x
where:
- T1=30∘C (temperature at one end),
- T2=20∘C (temperature at the other end),
- L=100cm (length of the rod),
- x is the distance from the higher temperature end.
Step 4: Substitute the Values
Substituting the known values into the equation:
T(40)=30+(20−30100)⋅40
Step 5: Calculate the Temperature
Now, calculate the term inside the parentheses:
20−30100=−10100=−0.1
Now substitute this back into the equation:
T(40)=30+(−0.1)⋅40
T(40)=30−4=26∘C
Final Answer
The temperature at the 40th cm from the higher temperature end (30°C) is 26∘C.
---
We have a meter rod (100 cm) with one end at a temperature of 30∘C and the other end at 20∘C. We need to find the temperature at the 40th cm from the end that is at 30∘C.
- The length of the rod is 100cm.
- The distance from the higher temperature end (30°C) to the point of interest (40 cm) is 40cm.
In steady state, the temperature T at a distance x from the higher temperature end can be expressed as:
T(x)=T1+(T2−T1L)x
where:
- T1=30∘C (temperature at one end),
- T2=20∘C (temperature at the other end),
- L=100cm (length of the rod),
- x is the distance from the higher temperature end.
Substituting the known values into the equation:
T(40)=30+(20−30100)⋅40
Now, calculate the term inside the parentheses:
20−30100=−10100=−0.1
Now substitute this back into the equation:
T(40)=30+(−0.1)⋅40
T(40)=30−4=26∘C
The temperature at the 40th cm from the higher temperature end (30°C) is 26∘C.
Topper's Solved these Questions
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL-II(C.W)
Explore 27 Videos
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:SINGLE ANSWER QUESTIONS
Explore 68 Videos
- THERMODYNAMICSBook:NARAYNAChapter:THERMODYNAMICSExercise:Exercise
Explore 187 Videos
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:STATEMENT TYPE QUESTION
Explore 23 Videos
Similar Questions
Heat is flowing through a rod of length 25.0cm having cross-sectional area 8.80cm2. The coefficient of thermal conductivity for the material of the rod is K=9.2×10−2kcals−1m−1.∘C−1. The Temperatures of the ends of the rod are 125∘C and 0∘C in the steady state. Calculate (i) temeprature gradient in the rod (ii) temperature of a point at a distance of 10.0cm from the hot end and (iii) rate of flow of heat.
View SolutionTwo rods of same dimensions, but made of different materials are joined end to end to end with their free end being maintained at 100∘C and 0∘C respectively. The temperature of the junction is 70∘C. Then the temperature of the junction if the rods are inerchanged will be equal to T∘C Find T:
View Solution
Knowledge Check
In a steady state of heat conduction the temperature of the ends A and B of a rod 100cm long per 0∘C and 100∘C The temperature of the rod at a point 60cm distant from the end A is .
A0∘CB40∘CC60∘CD100∘CThe end A of rod AB of length 1 m is maintained at 80∘C and the end B at 0∘C. The temperature at a distance of 60 cm from the end A is
A16∘CB32∘CC48∘CD64∘CThe temperature of hot and cold end of a 20 cm long rod in thermal steady state are at 100∘C and 20∘C respectively. Temperature at the centre of the rod is
A50∘CB60∘CC40∘CD30∘C
A copper rod 2 m long has a circular cross-section of radius 1 cm. One end is kept at 100∘C and the other at 0∘C. The surface is insulated so that negligible heat is lost through the surface. In steady state, find
(a) the thermal resistance of the bar
(b) the thermal current H
(c) the temperature gradient dTdx and
(d) the temperature at a distance 25 cm from the hot end.
Thermal conductivity of copper is 401 W/m−K.
View SolutionThree identical rods are joined in series as shown. Their thermal conductivities are K,K/2 and K/3 respectively. At steady, if the free ends of rods are at 100∘C and 20∘C respectively. Determine the temperature at two junction points. Also find the equivalent thermal conductivity.
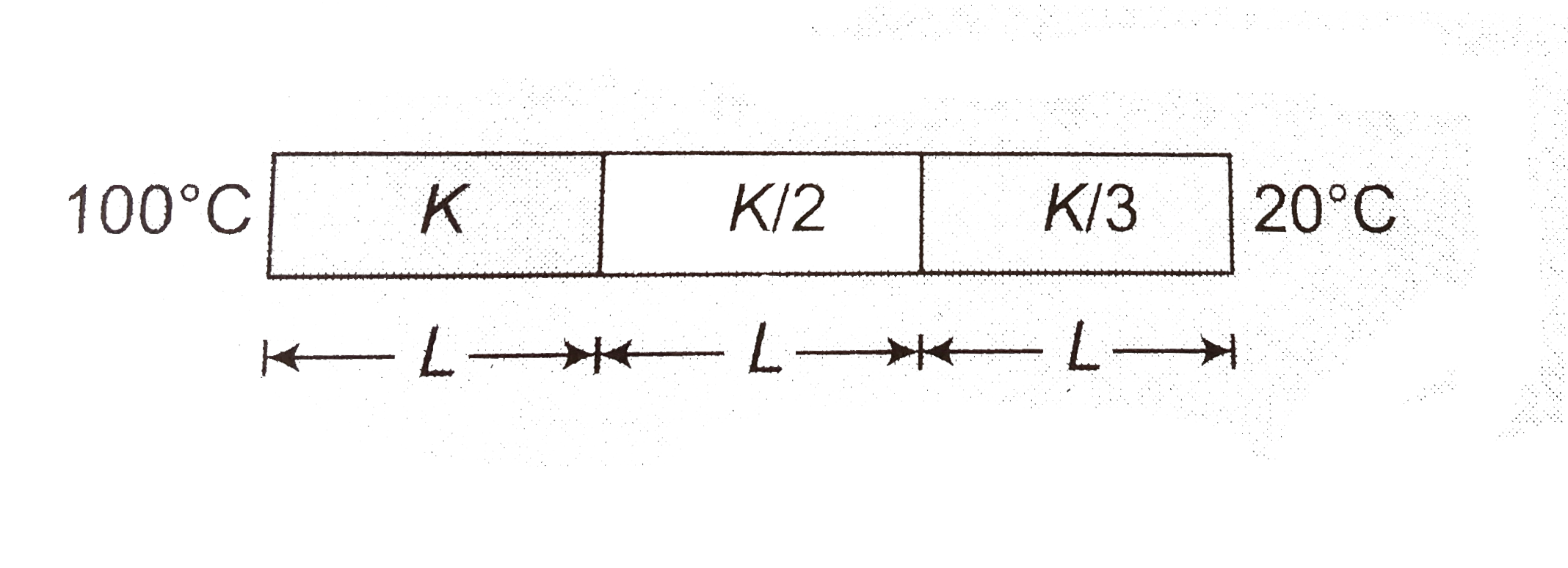
View SolutionSix identical conducting rods are connected as shown in figure. In steady state temperature of point ϕ1 is fixed at 100∘C and temperature of ϕ6 at −80∘C

Q. What is the temperature of ϕ2?
View SolutionThe ends of a thin bar are maintained at different temperatures. The temperature of the cooler end is 11∘C , while the temperature at a point 0.13m from the cooler end is 23∘C and the temperature of the warmer end is 48∘C. Assuming that heat flows only along the length of the bar ( the sides are insulated), find the length of the bar.
View SolutionA rod AB is 1m long. The temperature of its one end A is maintained at 100∘C and other end B at 10∘C, the temperature at a distance of 60 cm from point B is
View Solution

