0.5 mole of an ideal gas at constant temperature 27∘C kept inside a cylinder of length L and cross-section area A closed by a massless piston The cylinder is attached with a conducting rod of length L cross-section area (1/9)m2 and thermal conductivity k whise other end is maintained at 0∘C If piston is moved such that rate of heat flow through the conducing rod is constant then find velocity of piston when it is at height L/2 from the bottom of cylinder [Neglect any kind of heat loss from system
 .
.
k50R
k100R
k110R
k90R
The correct Answer is:B
ΔQΔt=ΔwΔt work done per unit time =kaθL
Power=F×Velocity=PAV'=nRTvAV
where V→ volume V'→ velocity
⇒0.5R(300)VAV'=kaθL
0.5R(300)AL2AV'=kaθL⇒V'=kaR(27300)=k100R .
Topper's Solved these Questions
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL-I(H.W)
Explore 19 Videos
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL-II(C.W)
Explore 27 Videos
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:SINGLE ANSWER QUESTIONS Passage -1
Explore 1 Video
- THERMODYNAMICSBook:NARAYNAChapter:THERMODYNAMICSExercise:Exercise
Explore 187 Videos
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:STATEMENT TYPE QUESTION
Explore 23 Videos
Similar Questions
As shownin the figure, 0.5mol of an ideal gas is kept inside an adiabatic cylinder of length L and cross-sectional area A closed by massless adiabatic piston. The cylinder is attached with a conducting rod of length L, crosssectionail area 1900m2 and thermal condactivity 415.5W m^(-1) K^(-1),whoseotherendisma∫a∈edat0^(circ) C.Theπs→nismovedsuchtˆthetemperatureofthegasrema∈sconstantat27^(circ) C.F∈dthevelocity(∈(mm) / (s))oftheπs→nwhenitisatbeightL / 2omthe⊥→mofcyl∈der.(Rodiswelllag≥dandhas¬ligib≤heat∩acity,R=8.31 (Jmol ^(-1) K^(-1) )
'(##CEN_KSR_PHY_JEE_C15_E01_034_Q22##)'
View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View Solution
Knowledge Check
0.5 mole of an ideal gas at constant temperature 27∘C kept inside a cylinder of length L and cross-section area A closed by a massless piston The cylinder is attached with a conducting rod of length L cross-section area (1/9)m2 and thermal conductivity k whose other end is maintained at 0∘C If piston is moved such that rate of heat flow through the conducing rod is constant then find velocity of piston when it is at height L/2 from the bottom of cylinder [Neglect any kind of heat loss from system
 .A(kR)m/secB(k10R)m/secC(k100R)m/secD(k1000R)m/sec
.A(kR)m/secB(k10R)m/secC(k100R)m/secD(k1000R)m/secA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKLIf l is the length, A is the area of cross-section and K the thermal conductivity, then the thermal resistance of the block is given by
AKlABlKACAKlDAKl
A steel farme (K=45Wm−1^(@)C^(-1)of→tal≤n>h60cmandcrosssectionarea0.02cm^(2),Formsthreesofa□.Theeeendsarema∫a∈edat20^(@)Cand40^(@)C . Find the rate of heat flow through a cross section of the frame.
View SolutionTwo ends of a conducting rod of varying cross-section are maintained at 200∘Cand0∘C respectively. In steady state :
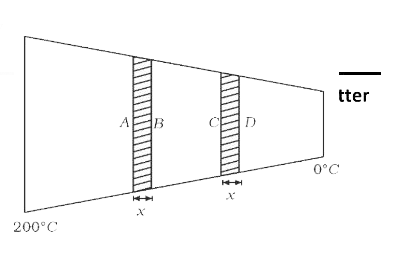
View SolutionTwo ends of a conducting rod of varying cross-section are maintained at 200∘C and 0∘C respectively. In steady state:

View SolutionOne end of a metal rod of length 1.0 m and area of cross section 100cm2 is maintained at . 100∘C. If the other end of the rod is maintained at 0∘C , the quantity of heat transmitted through the rod per minute is (Coefficient of thermal conductivity of material of rod =100W/m−K)
View SolutionA metal rod of length 'L' and cross-sectional area 'A' is heated through 'T'∘C What is the force required to prevent the expansion of the rod lengthwise ?
View Solution

