Three metal rods of coefficient of thermal conductivities K,2K,3K conducts heats of 3Q,2Q,Q per seconds through unit area then the ratio of temperature gradients .
9:3:1
9:1:1
3:1:1
1:1:1
The correct Answer is:A
Q=KA(Δθ)tl
(Δθl)∝QKletΔθl=X⇒X∝QK
X1:X2:X3=Q1K1:Q2K2:Q3K3 .
Topper's Solved these Questions
Similar Questions
Three rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below

Then , the temperature of the junction in steady - state is
View SolutionA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
View Solution
Knowledge Check
Two ends of area A of a uniform rod of thermal conductivity k are maintained at different but constant temperatures. At any point on the rod, the temperature gradient is dTdl. If I be the thermal current in the rod, then:
AI∝ABI∝dTdlCI∝A∘DI∝1(dTdl)Two identical rods with different thermal conductivities k1 & k2 and different temperatures are first placed along length and then along area, then the ratio of rates of heat flow in both cases is
Ak1+k2k1+k2B4k1k2(k1+k2)2C(k1+k2)24k1D4k1k2(k1+k2)2Three rods of same dimensions have thermal condutivity 3K,2K and K They are arranged as shown in Then the temperature of the junction in steady state is
 .A2003∘CB1003∘CC75∘CD81∘C
.A2003∘CB1003∘CC75∘CD81∘C
Three rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is
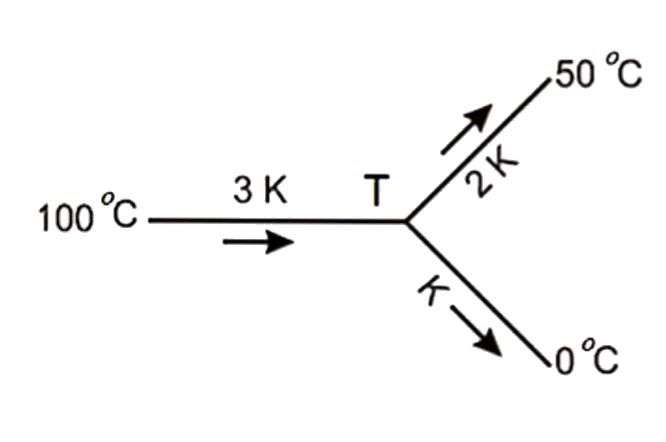
View SolutionRate of heat flow through two conducting rods of identiclal dimensions having thermal conductivities K1 and K2 and Q1 and Q2 when their ends are maintained at the same difference of temperature individually. When the two rods are joined in series with their ends maintained at the same temperature difference (as shown in the figure), the rate of heat flow will be

View SolutionTwo identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

View SolutionThree rods of lengths L,21 and 3L having thermal conductivities 3K,2K and K are connected end to end If cross sectional areas of three rods are equal If cross sectional areas of three rods are equal then equivalent thermal conductivity of the system is .
View SolutionTwo rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
View Solution

