Two rods one is semi circular of thermal conductivity K1 and otheir is straight of thermal conductivity K2 and of same cross sectional area are joined as shown in the The points A and B are maintained at same temperature difference. If rate of flow of heat is same in two rods then K1/K2 is
 .
.
2:π
1:2
π:2
3:2
The correct Answer is:C
(Qt)semicircularrod=(Qt)straightrod
K1A(Δθ)πr=K2A(Δθ)2r
r = radius of semi circle .
Topper's Solved these Questions
Similar Questions
In the steady state the two ends of a meter rod are at 30∘C and 20∘C the temperature at the 40thcm from the end at higher temperature is .
View SolutionAn amount Q of heat is added to a mono atomic ideal gas in a process in which the gas performs a work Q/2 on its surrounding. Find equation of the process.
View SolutionStatement-1 : Plane angle is a dimensionaless quantity.
Statement-2 : All supplementary quantities are dimensionless.
View SolutionTwo rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be

View SolutionTwo rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be

View SolutionTwo rods of the same length and diameter, having thermal conductivities K1 and K2, are joined in parallel. The equivalent thermal conductivity to the combinationk is
View SolutionTwo rods of same length and area of cross-section A_(1)" and" A_(2) have their ends at the same temperature. If K_(1) "and" K_(2) are their thermal conductivities, c_(1) "and" c_(2) are their specific heats and d_(1) "and "d_(2) are their densities, then the rate of flow of heat is the same in both the rods if
View SolutionTwo identical rods with different thermal conductivities k1 & k2 and different temperatures are first placed along length and then along area, then the ratio of rates of heat flow in both cases is
View SolutionTwo rods of length d1 and d2 and coefficients of thermal conductivites K1 and K2 are kept touching each other. Both have the same area of cross-section. The equivalent thermal conductivity.
View SolutionCondider two rods of same length and different specific heats (s_(1), s_(2)) , thermal conductivities (K_(1), K_(2)) and areas of cross-section (A_(1), A_(2)) and both having temperatures (T_(1), T_(2)) at their ends. If their rate of loss of heat due to conduction are equal, then
View SolutionTwo different metal rods of the same length have their ends kept at the same temperature theta_(1) , and theta_(2) with theta_(2) gt theta_(1) . If A_(1) and A_(2) are their cross-sectional areas and K_(1) and K_(2) their thermal conductivities, the rate of flow of heat in the two rods will be the same it:
View SolutionTwo metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
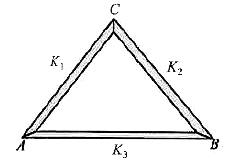
View SolutionThree rods of same dimensions are arranged as shown in the figure. They have thermal conductivities K1, K2 and K3. The points A and B are maintained at different temperatures. For the heat to flow at the same rate along ACB and AB,
View Solution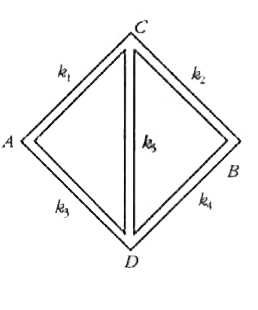
Five rods of same dimensions are arranged as shown in the figure. They have thermal conductivities k1,k2,k3,k4andk5 when points A and B are maintained at different temperatures. No heat flows through the central rod if
View SolutionTwo rods of same length and areas of cross-section A1 and A2 have their ends maintained at same temperature. If K1 and K2 are their thermal conductivities, c1 and c2 are the specific heats of their material and ρ1,ρ2 their densities, then for the rate of flow by conduction through them to be equal
View Solution

