Two rods of same length and area of cross-section A1 andA2 have their ends at the same temperature. If K1andK2 are their thermal conductivities, c1andc2 are their specific heats and d1and d2 are their densities, then the rate of flow of heat is the same in both the rods if
A1A2=−k1k2
A1A2=k1c1d1k2c2d2
A1A2=k2c1d1c2d2k1
A1A2=k2k1
Step by step video & image solution for Two rods of same length and area of cross-section A_(1)" and" A_(2) have their ends at the same temperature. If K_(1) "and" K_(2) are their thermal conductivities, c_(1) "and" c_(2) are their specific heats and d_(1) "and "d_(2) are their densities, then the rate of flow of heat is the same in both the rods if by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
View SolutionIn the following situations, the length and area of cross-section of each rod is same. Find temperature θ at junction of rods.
(a)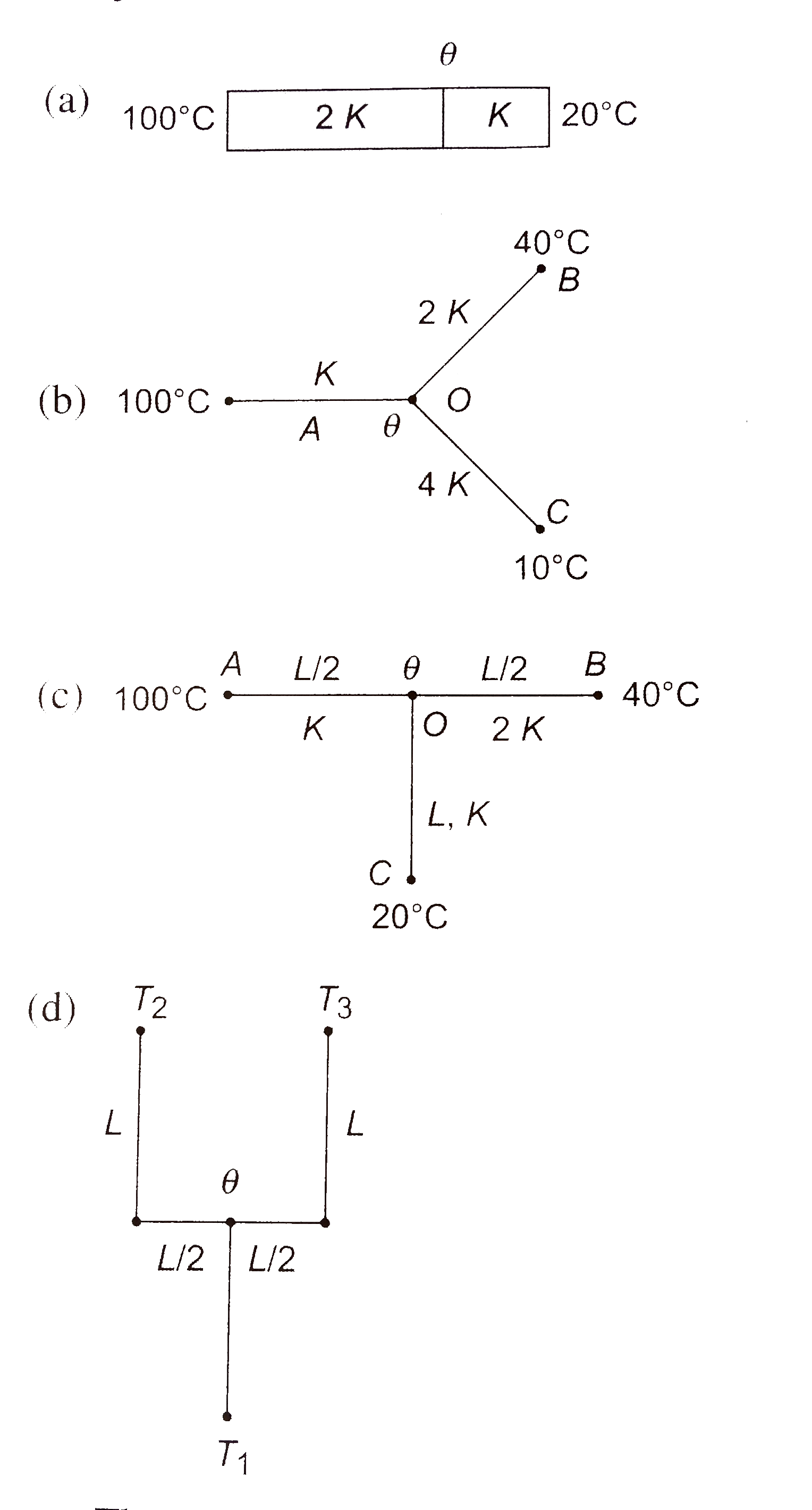
(b)
(c )
(d)
The thermal conductivity of each rod is K.
View Solution
Knowledge Check
Two rods of same length and areas of cross section A1 and A2 have their ends at same temperature. If K1 and K2 are their thermal conductivities, C1 and C2 their specific heats and ρ1 and ρ2 are their densities, then the condition that rate of flow of heat is same in both the rods is
AA1/A2=K1/K2BA1/A2=K1C1ρ1/K2C2ρ2CA1/A2=K2C1ρ1/K1C2ρ2DA1/A2=K2/K1Two rods of the same length and areas of cross-section A1 and A2 have their ends at the same temperature. K1 and K2 are the thermal conductivities of the two rods. The rate of flow of heat is same in both the rods if-
AA1A2=L1K2BA1A2=K2K1CA1A2=K1K2Dplaced in hot oilTwo different metal rods of equal lengths and equal areas of cross-section have their ends kept at the same temperature θ1 and θ2. if K1 and K2 are their thermal conductivities, ρ1 and ρ2 their densities and S1 and S2 their specific heats, then the rate of flow of heat in the two rods will be the same if:
Ak1k2=ρ1s1ρ1s2Bk1k2=ρ1s2ρ2s1Ck1k2=θ1θ2Dk1=k2
Two different metal rods of the same length have their ends kept at the same temperature θ1, and θ2with θ2>θ1. If A1 and A2 are their cross-sectional areas and K1 and K2 their thermal conductivities, the rate of flow of heat in the two rods will be the same it:
View SolutionTwo rods A and B are of equal lengths. Their ends of kept between the same temperature and their area of cross-section are A1 and A2 and thermal conductivities K1 and K2. The rate of heat transmission in the two rods will be equal, if
View SolutionTwo identical rods with different thermal conductivities k1 & k2 and different temperatures are first placed along length and then along area, then the ratio of rates of heat flow in both cases is
View SolutionTwo rods of the same length and diameter, having thermal conductivities K1 and K2, are joined in parallel. The equivalent thermal conductivity to the combinationk is
View SolutionThree metal rods of same lenghs and same area of cross sections having conductivities 1,2,3, units are connected in series Then their effective conductivity will be .
View Solution
