
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
√7T0
√5T0
2T0
√3T0
The correct Answer is:B
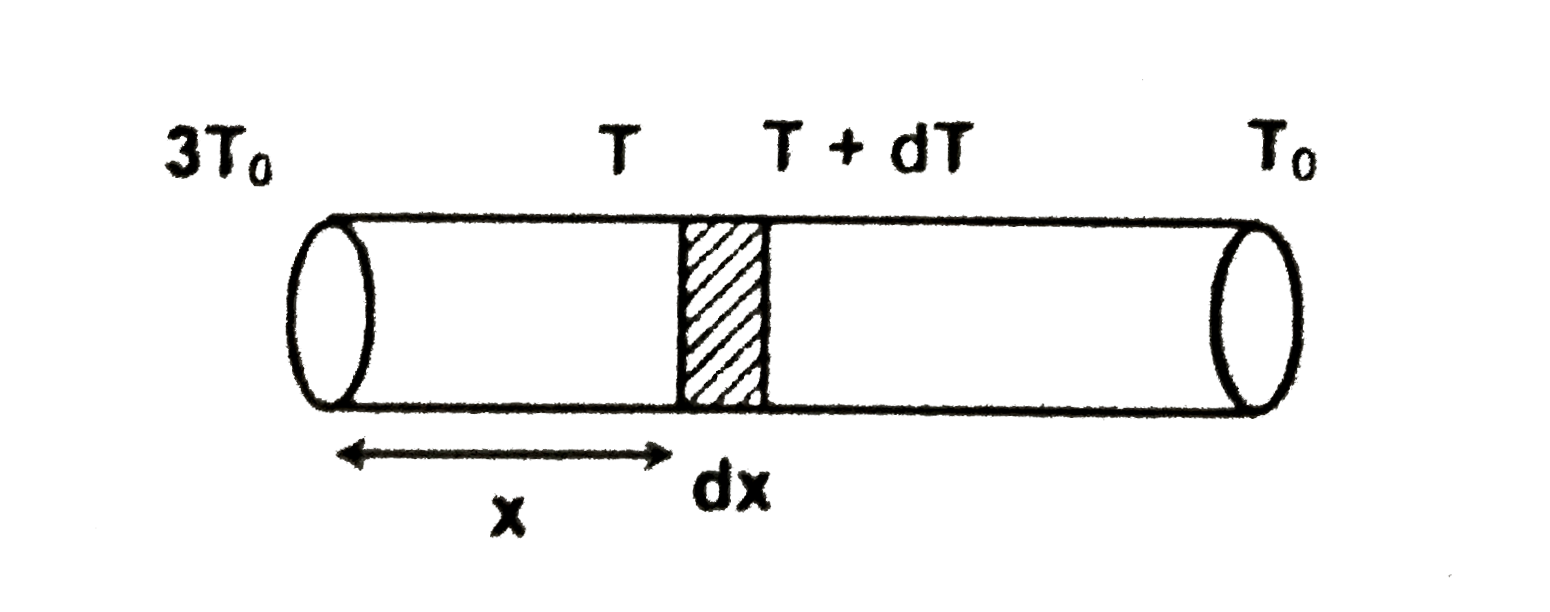
Ins steady state
ΔQΔt=−kAdTdx
ΔQΔt=−αTAdTdx
ΔQΔtl∫0dx=−αA∫T03T0TdT
ΔQΔtl=4αAT20 ...(i)
Similarly,
ΔQΔtl/2∫0dx=−αAT∫3T0TdT
ΔQΔtl2=αA(9T20−T2)2 ...(ii)
Dividing (ii) by (i)
9T20−T2=4T20
T2=5T20
T2=5T20
T=√5T0.
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
Two ends of a rod of non uniform area of cross section are maintained at temperature T1and T2 (T1>T2) as shown in the figure
If l is heat current through the cross-section of conductor at distance x from its left face, then the variation of l with x is best represented by
View SolutionA rod of length L with sides fully insulated is made of a material whose thermal conductivity K varies with temperature as K=αT where α is constant. The ends of rod are at temperature T1 and T2(T2>T1) Find the rate of heat flow per unit area of rod .
View Solution
Knowledge Check
One end of a metal rod is kept in a furnce. In steady state, the temperature of the rod
AincreasesBdecreasesCremains constantDis non uniform.The two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
AdQdt=KL(T1−T2)ABdQdt=KL(T1−T2)LACdQdt=KLA(T1−T2)DdQdt=KA(T1−T2)LTwo rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature (θ) of the interface will be -
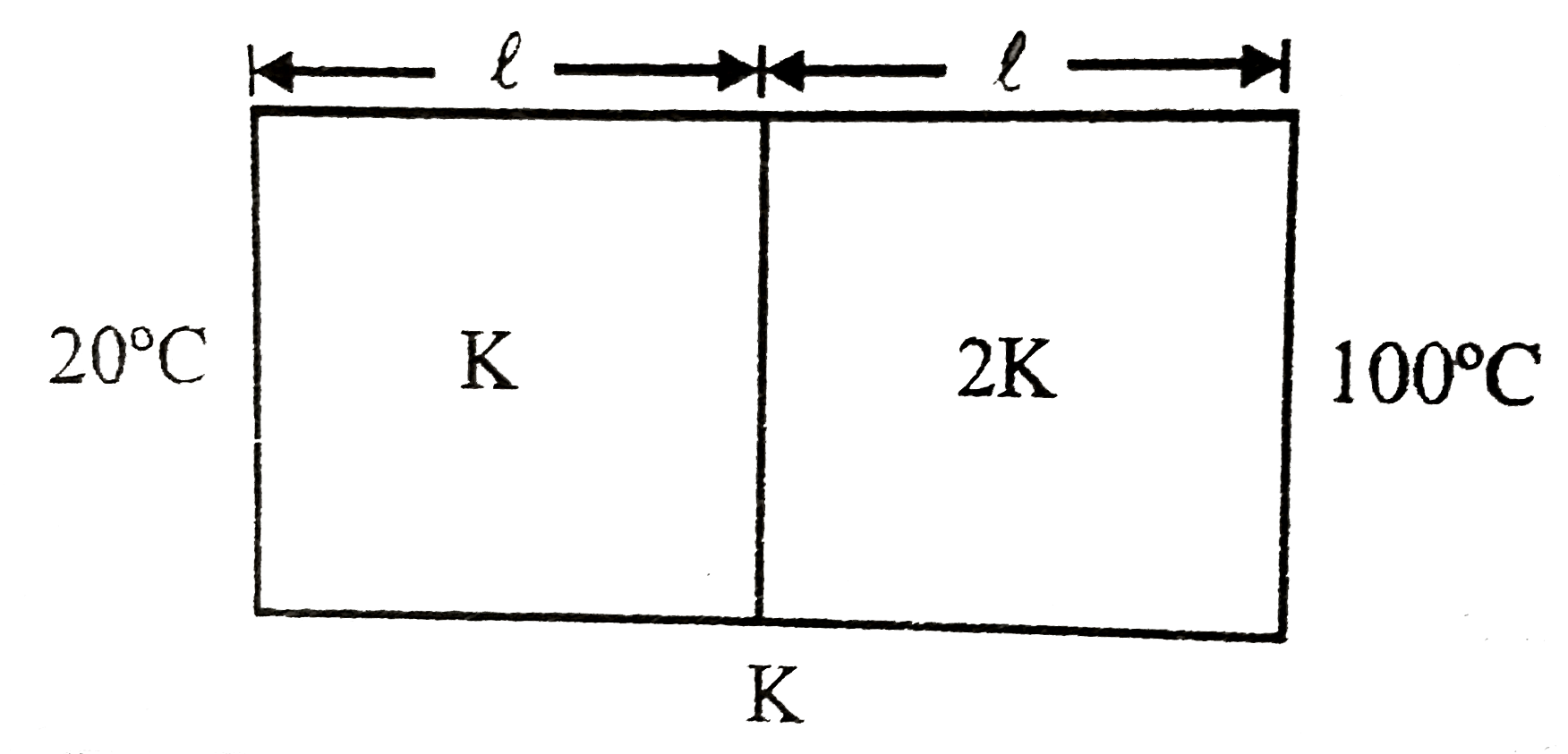 A60∘CB73.3∘CC46.7∘CD37.3∘C
A60∘CB73.3∘CC46.7∘CD37.3∘C
A conducting cylindrical rod of uniform cross-sectional area is kept between two large chambers which are at temperatures 100∘C and 0∘C, respectively. The cconductivety of the rod increases with x, where x is distance from 100∘C end. The temperature profile of the rod in steady -state will be as

View SolutionA rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
View SolutionA rod of length l and cross sectional area A has a variable conductivity given by K=αT, where α is a positive constant T is temperatures in Kelvin. Two ends of the rod are maintained at temperatures T1 and T2(T1>T2). Heat current flowing through the rod will be
View SolutionA rod of length l (laterally thermally insulated) of the uniform cross sectional area A consists of a material whose thermal conductivity varies with temperature as K=K0a+bT' where K0, a and b are constants. T1 and T2(<T1) are the temperatures of the ends of the rod. Then, the rate of flow of heat across the rod is
View SolutionTwo rods A and B of same cross sectional are A and length l connected in series between a source
(T1=100∘C) and a sink (T2=0∘C) as shown in The rod is laterally insulated

If AA and TB are the temperature drops across temperature gradients the rod A and B then .
View Solution
