The space between two thin concentric metallic spherical shells of radii a and b is filled with a thermal conducting medium of conductivity k. The inner shell is maintained at temperature T1 and outer is maintained at a lower temperatureT2 . Calculate the rate of flow of heat in radially outward direction through the medium.
To solve the problem of calculating the rate of flow of heat in the radially outward direction through the medium between two concentric metallic spherical shells, we can follow these steps:
1. Understand the Setup:
- We have two concentric metallic spherical shells with radii a (inner shell) and b (outer shell).
- The inner shell is maintained at temperature T1 and the outer shell at temperature T2 (where T1>T2).
- The space between the shells is filled with a thermal conducting medium of conductivity k.
2. Use Fourier's Law of Heat Conduction:
- According to Fourier's law, the rate of heat transfer (dQdt) through a medium is given by:
dQdt=−kAdTdr
- Here, A is the surface area through which heat is being transferred, and dTdr is the temperature gradient.
3. Determine the Surface Area:
- The surface area A of a sphere at radius r is:
A=4πr2
4. Consider an Elementary Shell:
- Consider an infinitesimally thin spherical shell of radius r and thickness dr.
- The temperature difference across this shell is dT and the thickness is dr.
5. Set Up the Heat Flow Equation:
- The heat flow through the shell can be expressed as:
dQdt=−k⋅4πr2⋅dTdr
6. Assume Steady State:
- In steady state, the heat flow dQdt is constant. Let’s denote it as IH:
IH=−k⋅4πr2⋅dTdr
7. Integrate the Equation:
- Rearranging gives:
IH⋅dr=−k⋅4πr2⋅dT
- Integrating both sides from r=a to r=b and T=T1 to T=T2:
IH∫badr4πr2=−k∫T2T1dT
8. Perform the Integration:
- The left-hand side integrates to:
IH4π(−1r)ba=IH4π(−1b+1a)
- The right-hand side integrates to:
−k(T2−T1)
9. Set the Two Integrals Equal:
- Equating both sides gives:
IH4π(1a−1b)=k(T1−T2)
10. Solve for IH:
- Rearranging for IH:
IH=4πk(T1−T2)(1a−1b)−1
- This can be simplified to:
IH=4πk(T1−T2)abb−a
Final Answer:
The rate of flow of heat in the radially outward direction through the medium is:
dQdt=4πk(T1−T2)abb−a
- We have two concentric metallic spherical shells with radii a (inner shell) and b (outer shell).
- The inner shell is maintained at temperature T1 and the outer shell at temperature T2 (where T1>T2).
- The space between the shells is filled with a thermal conducting medium of conductivity k.
- According to Fourier's law, the rate of heat transfer (dQdt) through a medium is given by:
dQdt=−kAdTdr
- Here, A is the surface area through which heat is being transferred, and dTdr is the temperature gradient.
- The surface area A of a sphere at radius r is:
A=4πr2
- Consider an infinitesimally thin spherical shell of radius r and thickness dr.
- The temperature difference across this shell is dT and the thickness is dr.
- The heat flow through the shell can be expressed as:
dQdt=−k⋅4πr2⋅dTdr
- In steady state, the heat flow dQdt is constant. Let’s denote it as IH:
IH=−k⋅4πr2⋅dTdr
- Rearranging gives:
IH⋅dr=−k⋅4πr2⋅dT
- Integrating both sides from r=a to r=b and T=T1 to T=T2:
IH∫badr4πr2=−k∫T2T1dT
- The left-hand side integrates to:
IH4π(−1r)ba=IH4π(−1b+1a)
- The right-hand side integrates to:
−k(T2−T1)
- Equating both sides gives:
IH4π(1a−1b)=k(T1−T2)
- Rearranging for IH:
IH=4πk(T1−T2)(1a−1b)−1
- This can be simplified to:
IH=4πk(T1−T2)abb−a
The rate of flow of heat in the radially outward direction through the medium is:
dQdt=4πk(T1−T2)abb−a
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.7
1 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.8
1 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.5
1 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
Two thin metallic spherical shells of radii r1andr2(r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells. Is maintained at temperature θ1 .and the outer shell at temperature θ2(θ1<θ2). Calculate the rate at which heat flows radially through the material.

View SolutionA tapering rod of length L has cross sectional radii of a and b(<a) at its two ends. Its thermal conductivity is k. The end with radius a is maintained at a higher temperature T1 and the other end is maintained at a lower temperature T2. The curved surface is insulated.
(i) At which of the two points–1 and 2– shown in the figure will the temperature gradient be higher?
(ii) Calculate the thermal resistance of the rod.
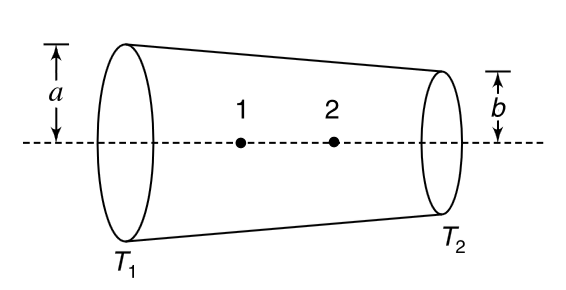
View Solution
Knowledge Check
A slab of material has area A, thickness L, and thermal conducitivy k. One of its surface (P ) is maintained at temperature T1 and the other surface (Q ) is maintained at a lower temperature T2. The rate of heat flow from P to Q is :
AkA(T1−T2)L2BkL(T1−T2)ACkL(T1−T2)LDk(T1−T2)(LA)
The space between two concentric conducting spherical shells of radii b=1.70 cm and a=1.20 cm is filled with a substance of dielectric constant k=6.91 A. A potential difference V=73.0 V is applied across the inner and outer shells Determine (a) the capacitance of the device (b) the free charge q on the inner shell, and (c) the charge q induced along the surface of the inner shell?
View SolutionThere are two concentric metallic shells of negligible thickness of radii 5 cm and 20 cm. The region between the two shells is filled with a medium of thermal conductivity k. The temperature of inner and outer sphere is maintained at 5∘C and 10∘C respectively. If the heat current flowing from inner to outer sphere is 100 W, find the value of k.
View SolutionThere are two thin concentric conducting shells of radii a and b(a<b) . Equal charges Q given to each shell. Find the charge distribution on the inner and outer shell.
View SolutionNine identical conducting rods are arranged as shown in the figure. The ends A and B are maintained at temperatues T1 and T2. Calculate the ratio of rate of flow of heat across AD to that of EB in the given arrangement in steady state.
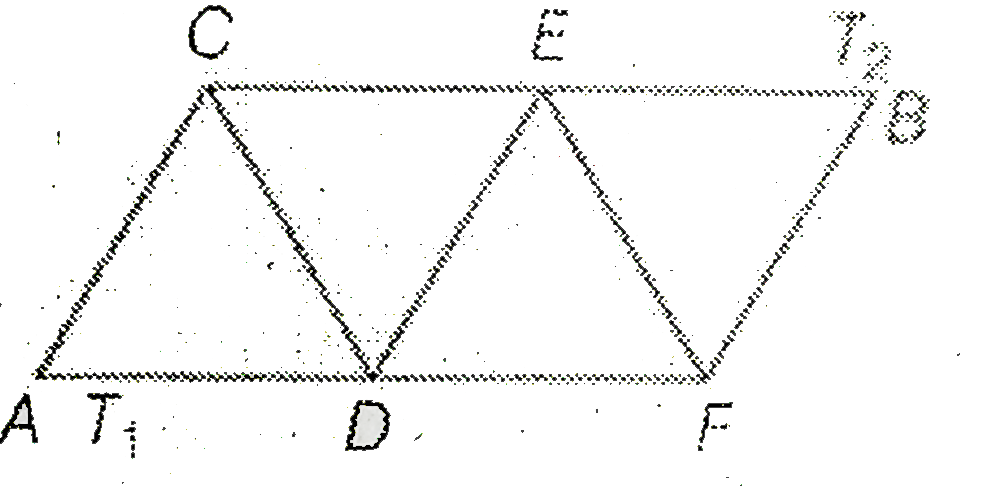
View SolutionThe space between two conducting concentric spheres of radii a and b(a<b) is filled up with homongeneous poorly conducting medium. The capacitance of such a system equals C. Find the resistivity of the medium if the potential difference between the spheres, when they are disconnected from an external voltage , decreases η-fold during the time interval Δt.
View Solution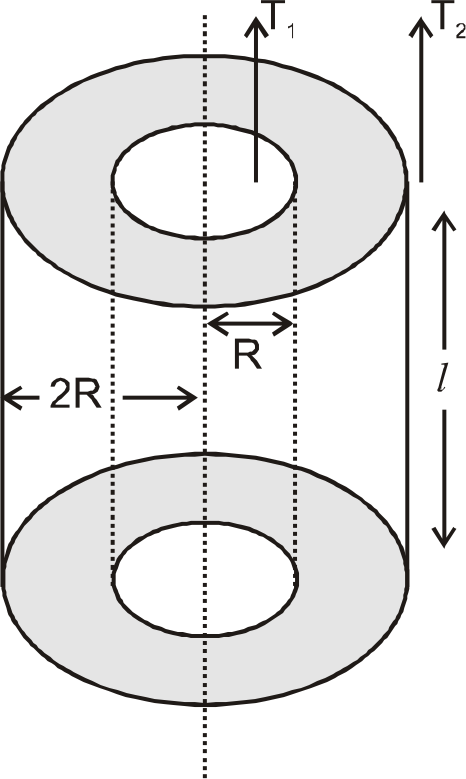
Inner surfaec of a cylindrical shell of length l and of material of thermal conductivity k is kept at constant temperature T1 and outer surface of the cylinder is kept at constant temperature T2 such that (T1>T2) as shown in figure. heat flows from inner surface to outer surface radially outward. inner and outer radii of the shell are R and 2R resspectively. Due to lack of space this cylinder has to be replaced by a smaller cylinder of length l2 inner and outer radii R4 and R respectively and thermal conductivity of material nk. if rate of radially outward heat flow remains same for same temperatures of inner and outer surface i.e., T1 and T2 then find the value of n.
View Solution(i) A cylindrical pipe of length L has inner and outer radii as a and b respectively. The inner surface of the pipe is at a temperature T1 and the outer surface is at a lower temperature of T2. Calculate the radial heat current if conductivity of the mate- rial is K.
(ii) A cylindrical pipe of length L has two layers of material of conduc- tivity K1 and K2. (see figure). If the inner wall of the cylinder is maintained at T1 and outer surface is at T2(<T1), calcu- late the radial rate of heat flow.
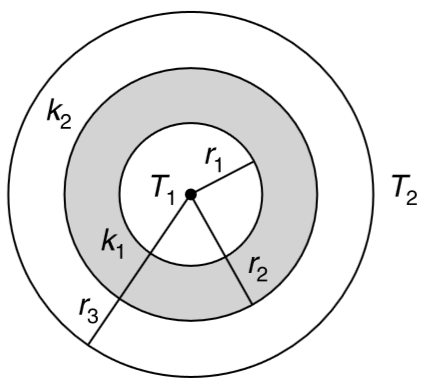
View Solution
