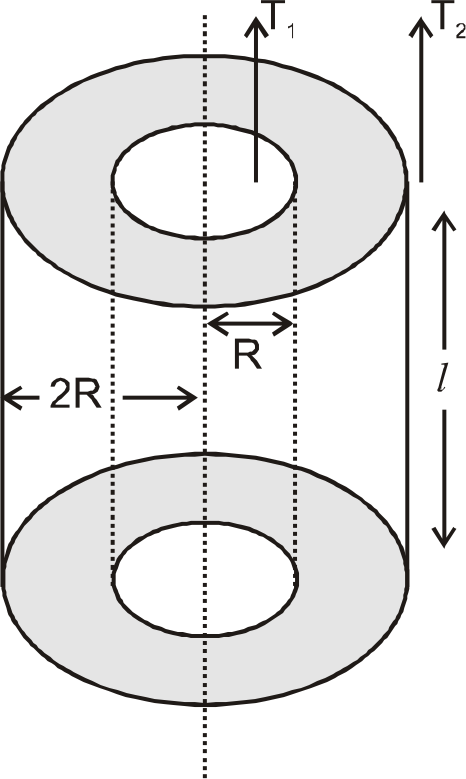
Inner surfaec of a cylindrical shell of length l and of material of thermal conductivity k is kept at constant temperature T1 and outer surface of the cylinder is kept at constant temperature T2 such that (T1>T2) as shown in figure. heat flows from inner surface to outer surface radially outward. inner and outer radii of the shell are R and 2R resspectively. Due to lack of space this cylinder has to be replaced by a smaller cylinder of length l2 inner and outer radii R4 and R respectively and thermal conductivity of material nk. if rate of radially outward heat flow remains same for same temperatures of inner and outer surface i.e., T1 and T2 then find the value of n.
H=−K.2πrldTdr
∫R2R1Hdr2πrl=−K∫T2T1dT
H=2πlk(T1−T2)ln(R2R1)
Hi=Hf
∴n=4
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased then
View SolutionIn the above example, if temperature of inner surface P is kept constant at θ1 and of the outer surface Q at θ2(<θ1). Then,
Find.
(a) rate of heat flow or heat current from inner surface to outer surface.
(b) temperature θ at a distance r(a<r<b) from centre.
View SolutionA spherical shell of inner radius R1 and outer radius R2 is having variable Where 'r' is the distance from the centre Two surface of the shell are maintained at temperature T1 respectively (T1<T2) The heat current flowing through the shell would be .
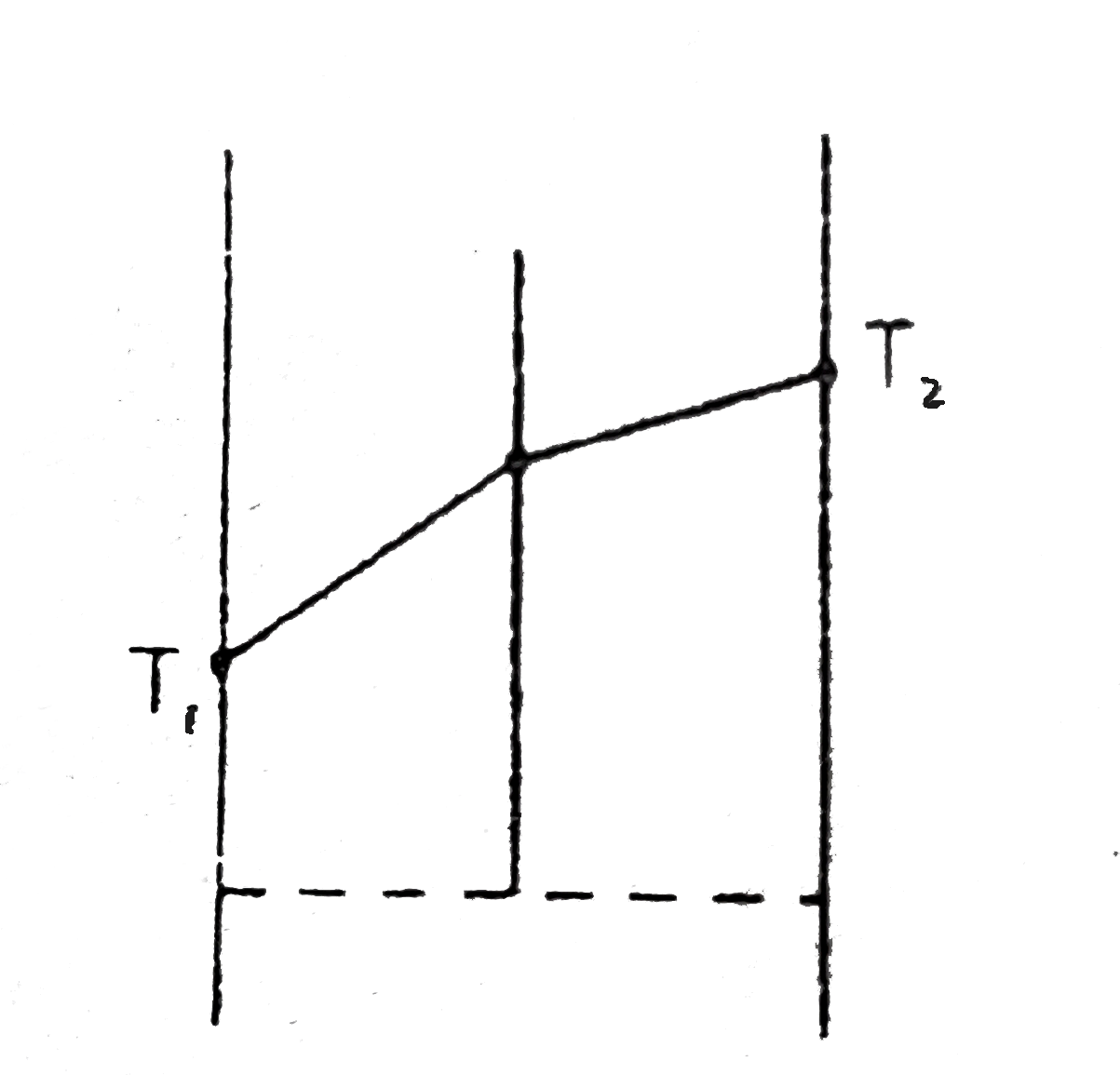
View SolutionThe wall of a house is made of two different materials of same thickness. The temperatures of the outer wall is T2 and that of inner wall is T1<T2. The temperature variation inside the wall as shown in the figure. Then :
View SolutionA thick spherical shell of inner and outer radii r and R respectively has thermal conductivity k=ρxn , where ρ is a constant and x is distance from the centre of the shell. The inner and outer walls are maintained at temperature T1 and T2(<T1)
(a) Find the value of number n (call it n0) for which the temperature gradient remains constant throughout the thickness of the shell.
(b) For n=n0, find the value of x at which the temperature is T1+T22
(c) For n=n0, calculate the rate of flow of heat through the shell.
View Solution(i) A cylindrical pipe of length L has inner and outer radii as a and b respectively. The inner surface of the pipe is at a temperature T1 and the outer surface is at a lower temperature of T2. Calculate the radial heat current if conductivity of the mate- rial is K.
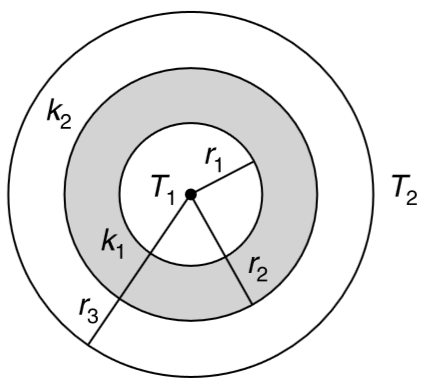
(ii) A cylindrical pipe of length L has two layers of material of conduc- tivity K1 and K2. (see figure). If the inner wall of the cylinder is maintained at T1 and outer surface is at T2(<T1), calcu- late the radial rate of heat flow.
View SolutionA thick cylindrical shell made of material of thermal conductivity k has inner and outer radii r and R respectively and its length is L. When the curved surface of the cylinder are lagged (i.e., given insulation cover) and one end is maintained at temperature T_(1) and the other end is maintained at T_(2)(lt T_(1)) , the heat current along the length of the cylinder is H. In another experiment the two ends are lagged and the inner wall and outer wall are maintained at T_(1) and T_(2) respectively. Find the radial heat flow in this case.
View SolutionA cylinder of radius R is surrounded by a cylindrical shell of inner radius R and oputer radius 2R. The thermal conductivity of the material of the inner cylinder si k_(1) and that of the outer cylinder is K_(2) ,Assumming no loss of heat , the effective thermal conductivity of the system for heat flowing along the length of the cylionder is :
View SolutionInner and outer surfaces of a cylinder are maintained at temperature 4T and T respectively. Heat flows radially from inner surface of radius R to outer surface of radius 4R. Radial distance from the center where temperature is 2T.
View SolutionThe space between two thin concentric metallic spherical shells of radii a and b is filled with a thermal conducting medium of conductivity k. The inner shell is maintained at temperature T1 and outer is maintained at a lower temperatureT2 . Calculate the rate of flow of heat in radially outward direction through the medium.
View SolutionA cylinder of radius R is surrounded by a cylindrical shell of inner radius R and oputer radius 2R. The thermal conductivity of the material of the inner cylinder is k1 and that of the outer cylinder is K2 ,Assumming no loss of heat , the effective thermal conductivity of the system for heat flowing along the length of the cylinder is :
View SolutionHeat flows radially outward through a spherical shell of outside radius R2 and inner radius R1. The temperature of inner surface of shell is θ1 and that of outer is θ2. At what radial distance from centre of shell the temperature is just half way between θ1 and θ2
View SolutionA spherical shell of inner radius R1 and outer radius R2 is having variable thermal conductivity given by K=a0T×r, where a0 is constant and T is temperature in kelvin and r is the distance from the centre. Two surface of the shell are maintained at temperature T1 (inner surface) and T2 (outer surface), respectively (T1>T2). The heat current flowing through the shell would be
View SolutionA thick spherical shell has two equally thick layers with conductivities for inner and outer layers nk and k respectively. If the interface temperature is arithmetic mean of inner and outer surface temperature of composite shell then value of n is (Assume inner radius R and other radius 2R for composite layer)
View Solution

