A thick spherical shell of inner and outer radii r and R respectively has thermal conductivity , where is a constant and x is distance from the centre of the shell. The inner and outer walls are maintained at temperature and
(a) Find the value of number n (call it ) for which the temperature gradient remains constant throughout the thickness of the shell.
(b) For , find the value of x at which the temperature is
(c) For , calculate the rate of flow of heat through the shell.
The correct Answer is:(a) (b)
Step by step video, text & image solution for A thick spherical shell of inner and outer radii r and R respectively has thermal conductivity k = (rho)/(x^(n)) , where rho is a constant and x is distance from the centre of the shell. The inner and outer walls are maintained at temperature T_(1) and T_(2) (lt T_(1)) (a) Find the value of number n (call it n_(0)) for which the temperature gradient remains constant throughout the thickness of the shell. (b) For n=n_(0), find the value of x at which the temperature is (T_(1)+T_(2))/(2) (c) For n = n_(0), calculate the rate of flow of heat through the shell. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two lead balls of mass m and 2 m are placed at a separation d. A third ball of mass m is placed at an unknown location on the line joining the first two balls such that the net gravitational force experienced by the first ball is 6Gm2d2 . What is the location of the third ball?
View SolutionA car manufacturer usually tells a optimum speed (V0) at which the car should be driven to get maximum mileage. In order to find the optimum speed for a new model, an engineer of the car company experimented a lot and finally plotted a graph between the extreme time t (defined as number of hours a tank full of petrol lasts) vs the constant speed V at which car was run.
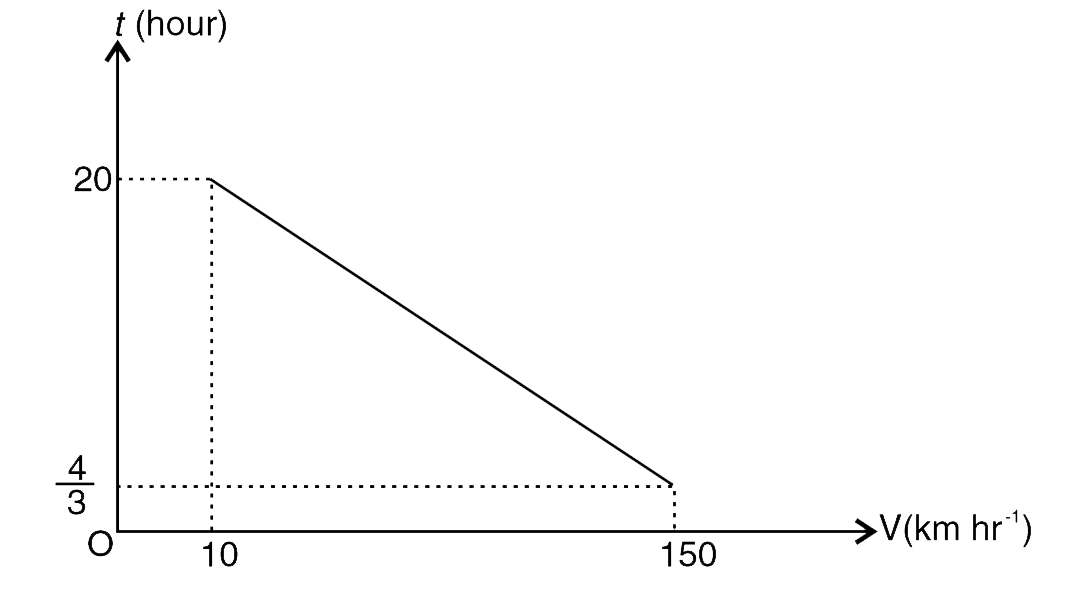
(a) Calculate the optimum speed V0 for this new model.
(b) If the fuel tank capacity of this car is 50 litre, what maximum mileage can be obtained from this car?
View Solution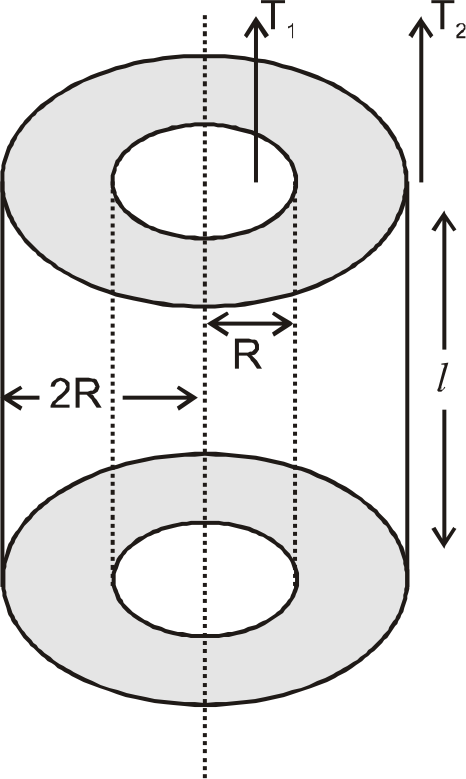
Inner surfaec of a cylindrical shell of length l and of material of thermal conductivity k is kept at constant temperature T1 and outer surface of the cylinder is kept at constant temperature T2 such that (T1>T2) as shown in figure. heat flows from inner surface to outer surface radially outward. inner and outer radii of the shell are R and 2R resspectively. Due to lack of space this cylinder has to be replaced by a smaller cylinder of length l2 inner and outer radii R4 and R respectively and thermal conductivity of material nk. if rate of radially outward heat flow remains same for same temperatures of inner and outer surface i.e., T1 and T2 then find the value of n.
View SolutionA spherical shell of inner radius R1 and outer radius R2 is having variable Where 'r' is the distance from the centre Two surface of the shell are maintained at temperature T1 respectively (T1<T2) The heat current flowing through the shell would be .
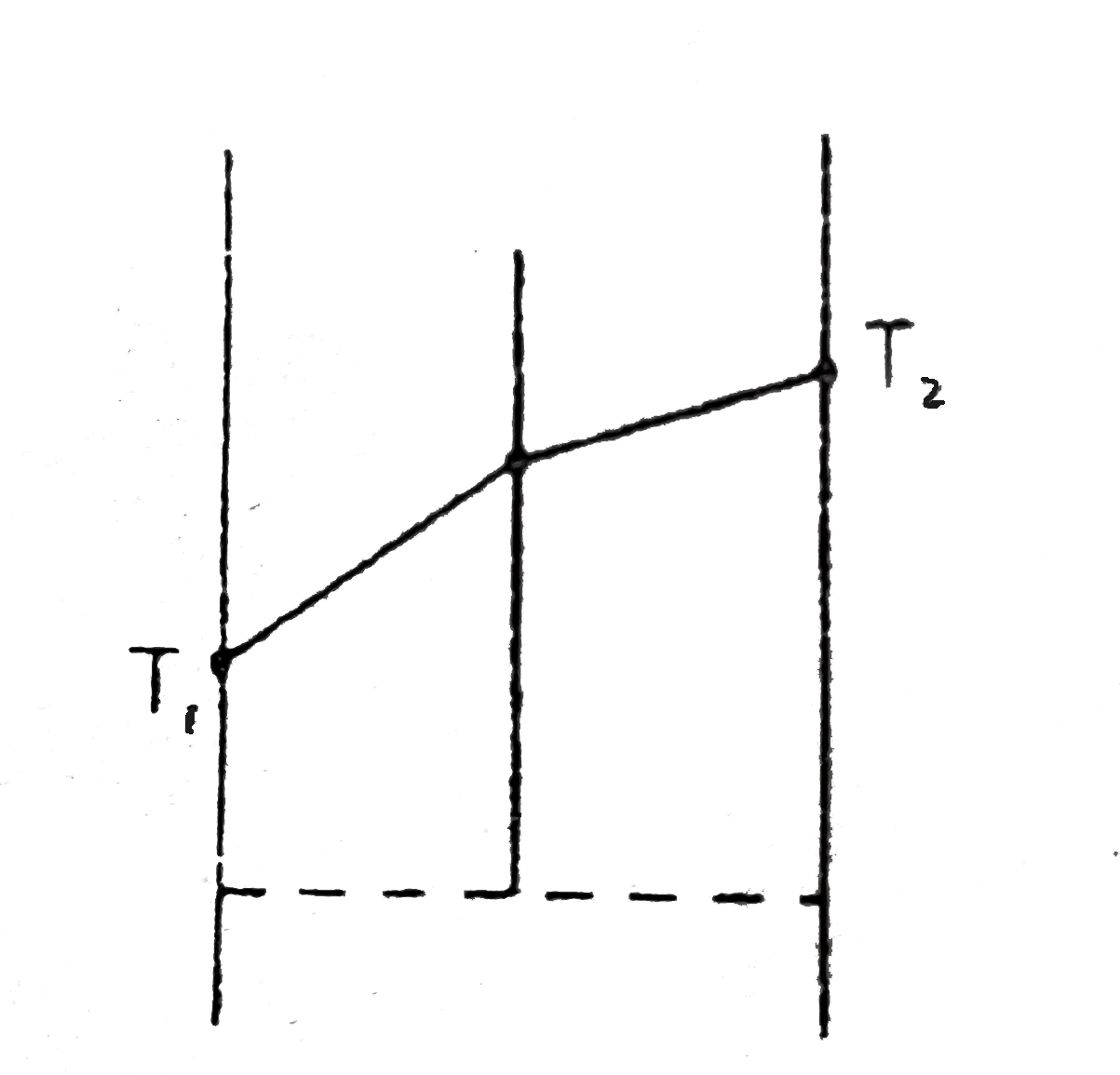
View SolutionThe wall of a house is made of two different materials of same thickness. The temperatures of the outer wall is T2 and that of inner wall is T1<T2. The temperature variation inside the wall as shown in the figure. Then :
View SolutionA thick cylindrical shell made of material of thermal conductivity k has inner and outer radii r and R respectively and its length is L. When the curved surface of the cylinder are lagged (i.e., given insulation cover) and one end is maintained at temperature T_(1) and the other end is maintained at T_(2)(lt T_(1)) , the heat current along the length of the cylinder is H. In another experiment the two ends are lagged and the inner wall and outer wall are maintained at T_(1) and T_(2) respectively. Find the radial heat flow in this case.
View SolutionTwo walls of thickness d and d and thermal conductivities k and k are in contact. In the steady state, if the temperature at the outer T_(1) and T_(2) , the temperature at the common wall is
View SolutionIn an arrangement of two concentric conducting shells, with centre at origin and radii a and b (a<b), charges Q1 and Q2 are given to inner and outer shell, then the potential V at a distance r from the origin is (r<a)
View SolutionThe space between two thin concentric metallic spherical shells of radii a and b is filled with a thermal conducting medium of conductivity k. The inner shell is maintained at temperature T1 and outer is maintained at a lower temperatureT2 . Calculate the rate of flow of heat in radially outward direction through the medium.
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d. The inner shell has total charge +2q, and the outer shell has charge +4q. (K=(1)/(4piepsilon_(0)))

Find the electric field in terms of q and the distance r from the common centre of the two shells for (i) r<a (ii) a<r<b
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d. The inner shell has total charge +2q, and the outer shell has charge +4q. (K=(1)/(4piepsilon_(0)))

Find the electric field in terms of q and the distance r from the common centre of the two shells for (i) b<r<c (ii) c<r<d
View SolutionIn Fig a conducting spherical shell of inner radius .x. and outer radius .y. is concentric with a larger conducting spherical shell of inner radius .a. and outer radius .b.. Inner shell has a total charge +3Q and the outer shell has a charge +5Q. Let r be the distance of any point from the common centre O.

View SolutionA hollow sphere of inner radius r_(0) and outer radius 2r_(0) is made of a uniform material of constant thermal conductivity K. The temperature with in the ball is maintained at 2T_(0) and outside the ball is T_(0) . If temperature at distance (3r_(0))/(2) from centre is (pT_(0))/(3) , then find the value of p.
View SolutionA spherical shell of inner radius R1 and outer radius R2 is having variable thermal conductivity given by K=a0T×r, where a0 is constant and T is temperature in kelvin and r is the distance from the centre. Two surface of the shell are maintained at temperature T1 (inner surface) and T2 (outer surface), respectively (T1>T2). The heat current flowing through the shell would be
View SolutionA conducting cylindrical shell inner radius R1 maintained at a temperature T1 and outer radius R2 maintained at a temperature T2 respectively. Thermal conductivity of the shell varies with distance from the axis as K=αr2. where α is constant. The temperature as a function of distance R from the axis of the cylinder is
View Solution

