A metal ball of mass 1.0 kg is kept in a room at 15∘C. It is heated using a heater. The heater supplies heat to the ball at a constant rate of 24 W. The temperature of the ball rises as shown in the graph. Assume that the rate of heat loss from the surface of the ball to the surrounding is proportional to the temperature difference between the ball and the surrounding. Calculate the rate of heat loss from the ball when it was at temperature of 20∘C.

The correct Answer is:4 Watt
Step by step video, text & image solution for A metal ball of mass 1.0 kg is kept in a room at 15^(@)C. It is heated using a heater. The heater supplies heat to the ball at a constant rate of 24 W. The temperature of the ball rises as shown in the graph. Assume that the rate of heat loss from the surface of the ball to the surrounding is proportional to the temperature difference between the ball and the surrounding. Calculate the rate of heat loss from the ball when it was at temperature of 20^(@)C. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Heat is supplied to a ice at a constant rate Temperature variation with time is as shown in figure. Then –
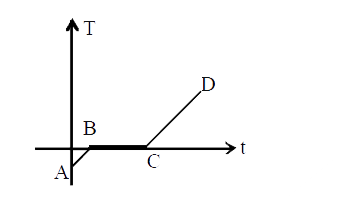
View SolutionA block is kept in a room which is at 20∘C. To raise the temperature of the block, heat is given to it at a constant rate of 600 watt (using an electric heater). The temperature of the block rises with time as shown in the graph. The slope of the graph at time t=0 is 3∘Cs−1. Once the temperature rises to 60∘C, the heater is switched off and another heater is switched on to maintain the temperature of the block at 60∘C. This new heater supplies heat at a constant rate of 100 watt. Assume that heat capacity of the block remains constant for the range of temperature involved.
(a) Explain why the slope of the given graph is decreasing with time.
(b) Calculate the heat capacity of the block.
(c) If the 100 W heater is also switched off, what will be initial rate of cooling of the block?
(d) Assuming that rate of heat loss by the block to the surrounding is proportional to difference in its temperature with surrounding, calculate the heat radiated per second by the block when it was at 30∘C.
View Solution
Knowledge Check
For a small temperature difference between the body and the surroundings, the relation between the rate of heat loss R and the temperature of the body is depicted by
A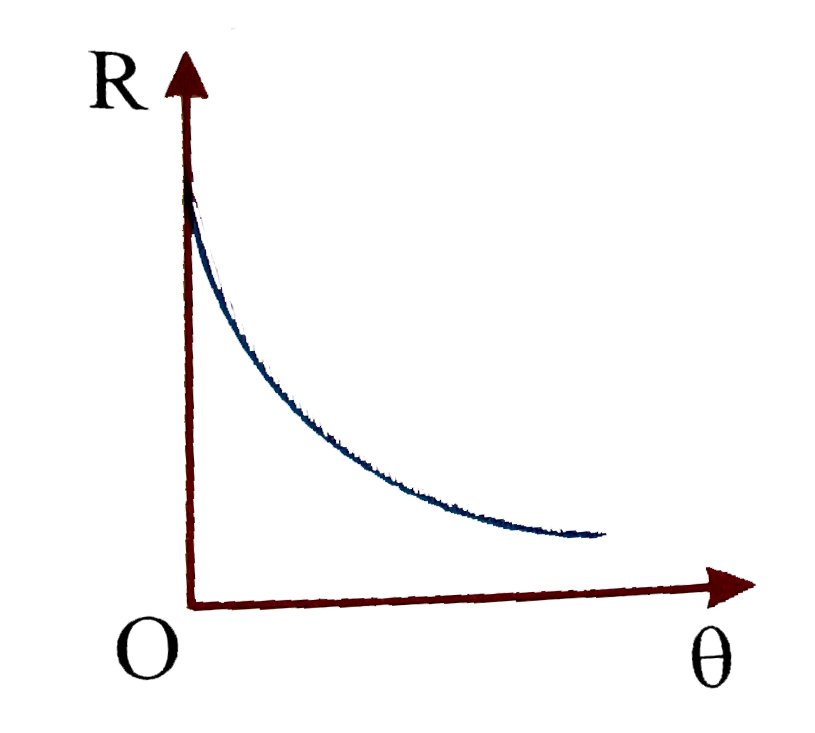 B
B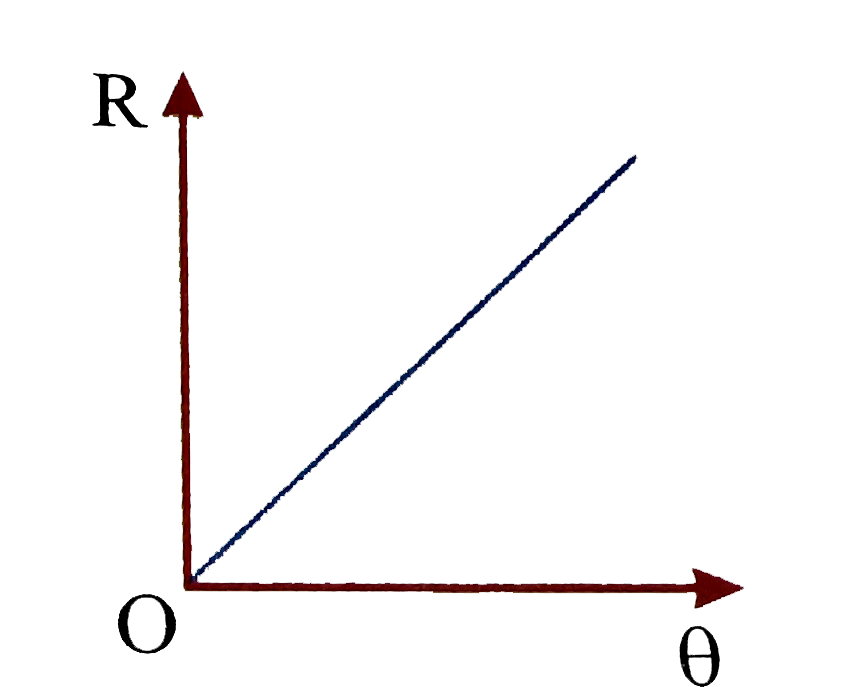 C
C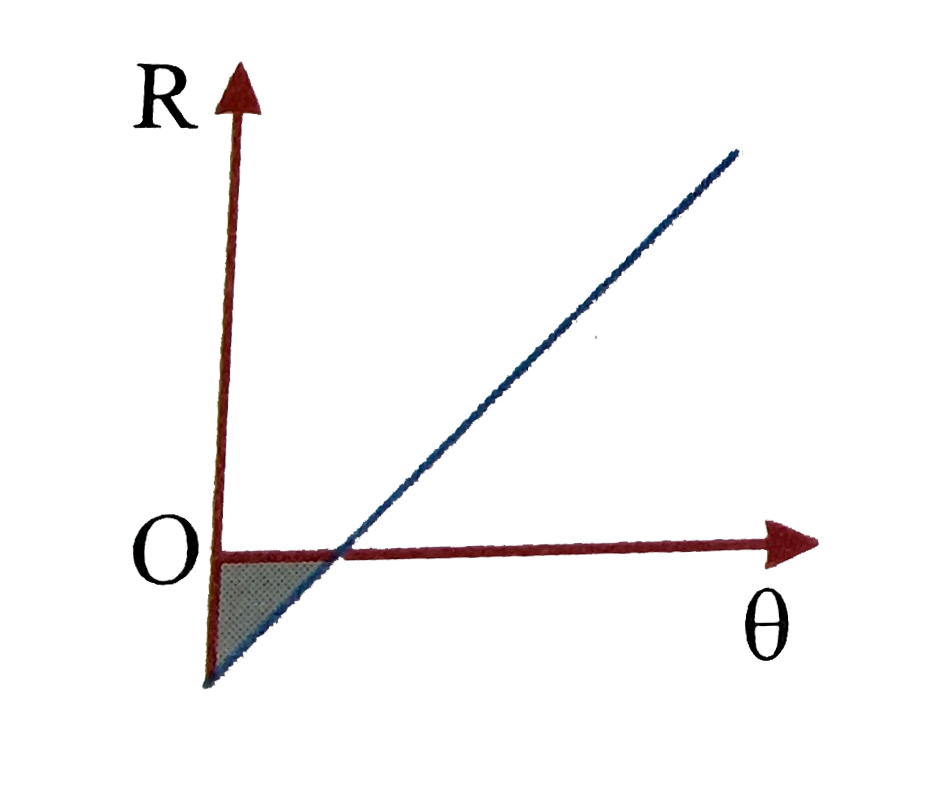 D
D
For a small temperature difference between the body and the surroundings the relation between the rate of loss heat R and the temperature of the body is depicted by
A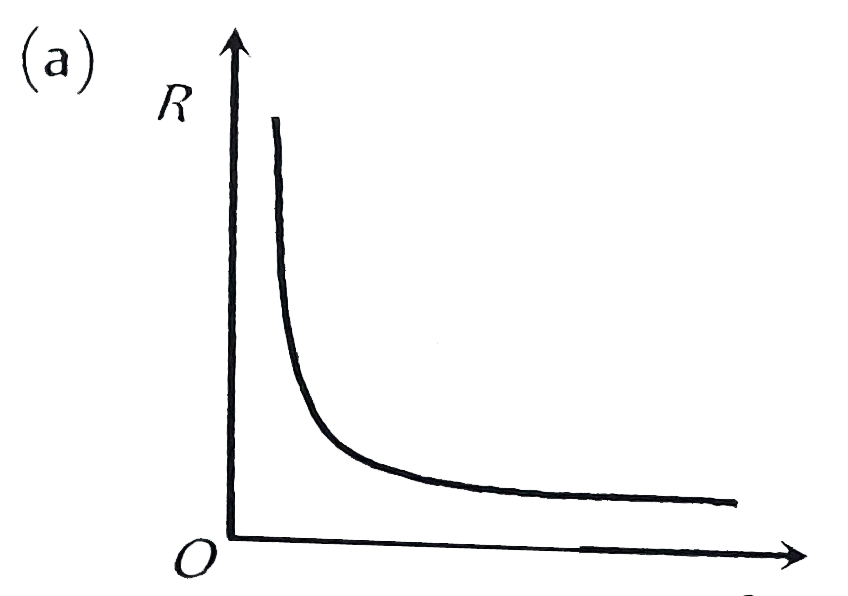 B
B C
C D
D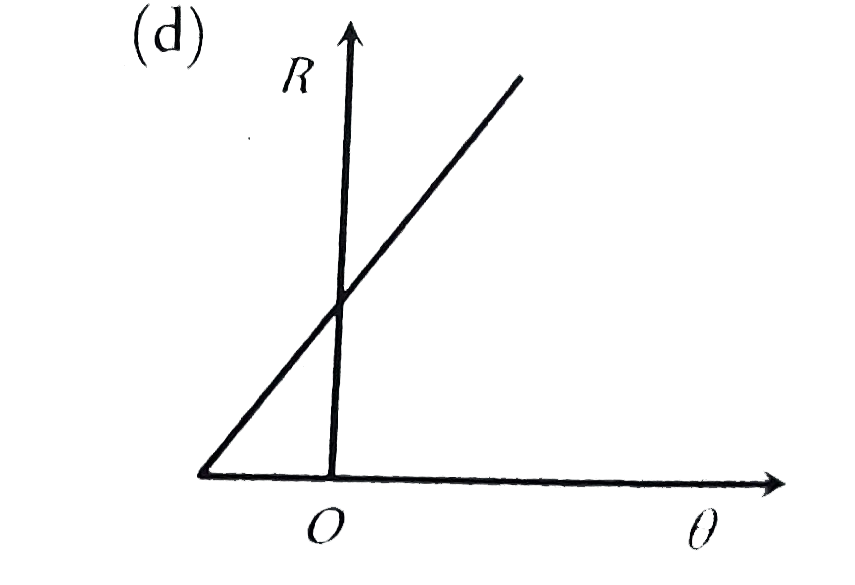
A metal ball of mass 2kg is heated means of a 40W heater in a room at 25∘C. The temperature of the ball beomes steady at 60∘C.
Assume that the temperature of the ball rises uniformly from 25∘C to 39∘Cin2 minutes. Find the total loss of heat to the surrounding during this period.A900JB940JC960JD1000J
A metal ball of 1kg mass is heated by a 20W heater in a room at20∘C. After some time temperature of ball becomes steady at 50'∘C. Find the rate of loss of heat by the ball to surrounding when its temperature becomes 50∘C. Also find the rate at which it looses heat to the surrounding when its temperature was 30∘C.
View SolutionA spherical metal ball of radius 1 cm is suspended in a room at 300 K temperature. Inside the sphere there is a battery operated heater which maintains the temperature of the ball at 1000 K. Find the power of the heater if emissivity of the metal ball is 0.3.
View SolutionA source of heat supplies heat at constant rate to a solid cube. The variatiion of the temperature of the cube with heat supplied is shown in figure. The portion DE of the graph represents conversion of
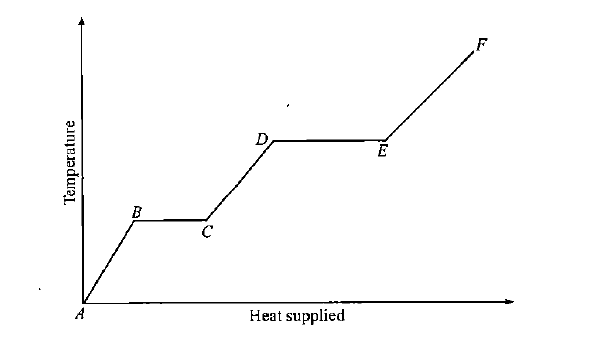
View SolutionAn electric heater supplies heat to a system at a rate of 120 W. if system performs work at a rate of 80 JS−1, the rate of increase in internal energy is
View SolutionA metal ball of mass 2kg is heated means of a 40W heater in a room at 25∘C. The temperature of the ball beomes steady at 60∘C.
Find the rate of loss of heat to the surrounding when the ball is at 60∘C.
View Solution

