A spherical shell is kept in an atmosphere at temperature T0. The wavelength corresponding to maximum intensity of radiation for the shell is λ0. A point source of constant power is switched on inside the shell. The power radiated by the source is P=04σSeT40 where S, e and σ are outer surface area of the shell, emissivity of the outer surface of the shell and Stefan’s constant respectively. Calculate the new wavelength (λ) corresponding to the maximum intensity of radiation from the shell. Assume that change in temperature (ΔT) of the shell is small compared to the ambient temperature T0.
The correct Answer is:1011λ0
Step by step video, text & image solution for A spherical shell is kept in an atmosphere at temperature T_(0). The wavelength corresponding to maximum intensity of radiation for the shell is lambda_(0). A point source of constant power is switched on inside the shell. The power radiated by the source is P = 04sigmaSeT_(0)^(4) where S, e and sigma are outer surface area of the shell, emissivity of the outer surface of the shell and Stefan’s constant respectively. Calculate the new wavelength (lambda) corresponding to the maximum intensity of radiation from the shell. Assume that change in temperature (DeltaT) of the shell is small compared to the ambient temperature T_(0). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Intensity of gravitational field inside the hollow spherical shell is
AVariableBminimumCmaximumDzeroA point source of heat of power P is placed at the centre of a thin spherical shell of a mean radius R. The material of the shell has thermal conductivity K. Calculate the thickness of the shell if the temperature difference between the outer and inner surfaces of the shell in steady - state is T.
A4πR2KT2PB3πR4KTPC4πR2KTPD2πR2KT3PA solid spherical conducting shell has inner radius a and outer radius 2a. At the center of the shell is located a point charge +Q. What must the excess charge of the shell be in order for the charge density on the inner and outer surface of the shell to be exactly equal?
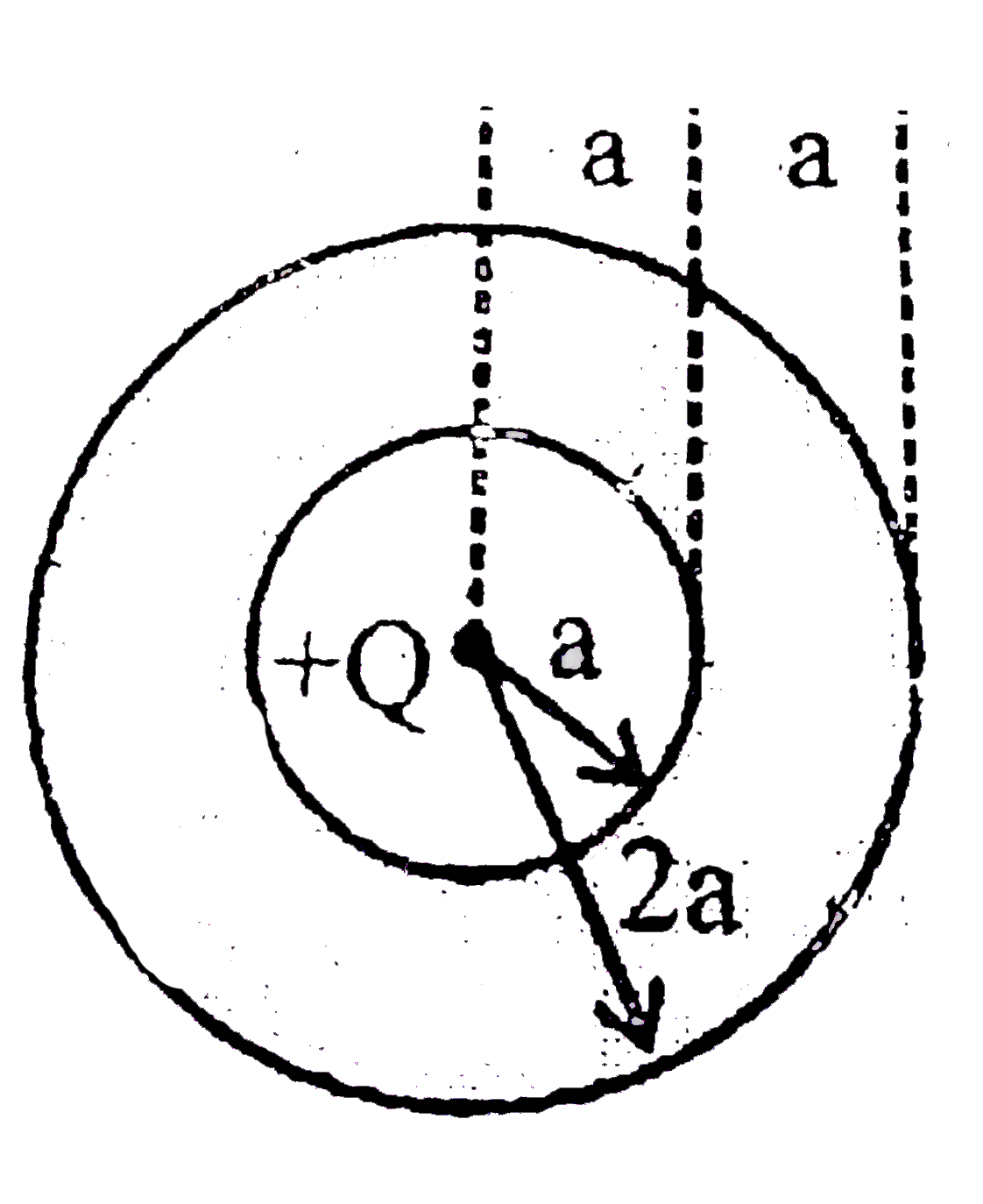 A−5QB+3QC−4QD+4Q
A−5QB+3QC−4QD+4Q
A spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
View SolutionA space station is covered by an envelope which is a blackened shell. The temperature of the envelope is T = 500 K that is constant due to the operation of applicances of the station. Determine the temperature of the shell if the station is enveloped by a thin spherical black screen of nearly the same radius as the radius of the shell. Assume that there are no radiations on this space station.
View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionA point source of heat of power P is placed at the centre of a spherical shell of mean radius R. The material of the shell has thermal conductivity K. If the temperature difference between the outer and inner surface of the shell in not to exceed T, the thickness of the shell should not be less than .......
View SolutionThe wavelength of the radiation emitted when the electron jumps from 4th shell to 2nd shell is
View Solution

