A plane surface A is at a constant temperature T1=1000K. Another surface B parallel to A, is at a constant lower temperature T2=300K. There is no medium in the space between two surfaces. The rate of energy transfer from A to B is equal to r1(Js). In order to reduce rate of heat flow due to radiation, a heat shield consisting of two thin plates C and D, thermally insulated from each other, is placed between A and B in parallel. Now the rate of heat transfer (in steady state) reduces to r2. Neglect any effect due to finite size of the surfaces, assume all surfaces to be black bodies and take Stefan’s constant σ=6×10−8Wm−2K−4. Area of all surfaces A=1m2.
(i) Find r1
(ii) Find the ratio r2r1
(iii)Find the ratio rE(2)r1 if temperature of A and B were 2000 K 600 K respectively.

The correct Answer is:(i) r1=59513W (ii) r2r1=13 (iii) r2r1=13
Step by step video, text & image solution for A plane surface A is at a constant temperature T_(1) = 1000 K. Another surface B parallel to A, is at a constant lower temperature T_(2) = 300 K. There is no medium in the space between two surfaces. The rate of energy transfer from A to B is equal to r_(1)(J/s). In order to reduce rate of heat flow due to radiation, a heat shield consisting of two thin plates C and D, thermally insulated from each other, is placed between A and B in parallel. Now the rate of heat transfer (in steady state) reduces to r_(2). Neglect any effect due to finite size of the surfaces, assume all surfaces to be black bodies and take Stefan’s constant sigma = 6 xx 10^(- )8 Wm^(- 2)K^(-4). Area of all surfaces A = 1m^(2). (i) Find r^(1) (ii) Find the ratio (r^(2))/(r^(1)) (iii)Find the ratio (r^E(2))/(r_(1)) if temperature of A and B were 2000 K 600 K respectively. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two lead balls of mass m and 2 m are placed at a separation d. A third ball of mass m is placed at an unknown location on the line joining the first two balls such that the net gravitational force experienced by the first ball is 6Gm2d2 . What is the location of the third ball?
View SolutionA car manufacturer usually tells a optimum speed (V0) at which the car should be driven to get maximum mileage. In order to find the optimum speed for a new model, an engineer of the car company experimented a lot and finally plotted a graph between the extreme time t (defined as number of hours a tank full of petrol lasts) vs the constant speed V at which car was run.
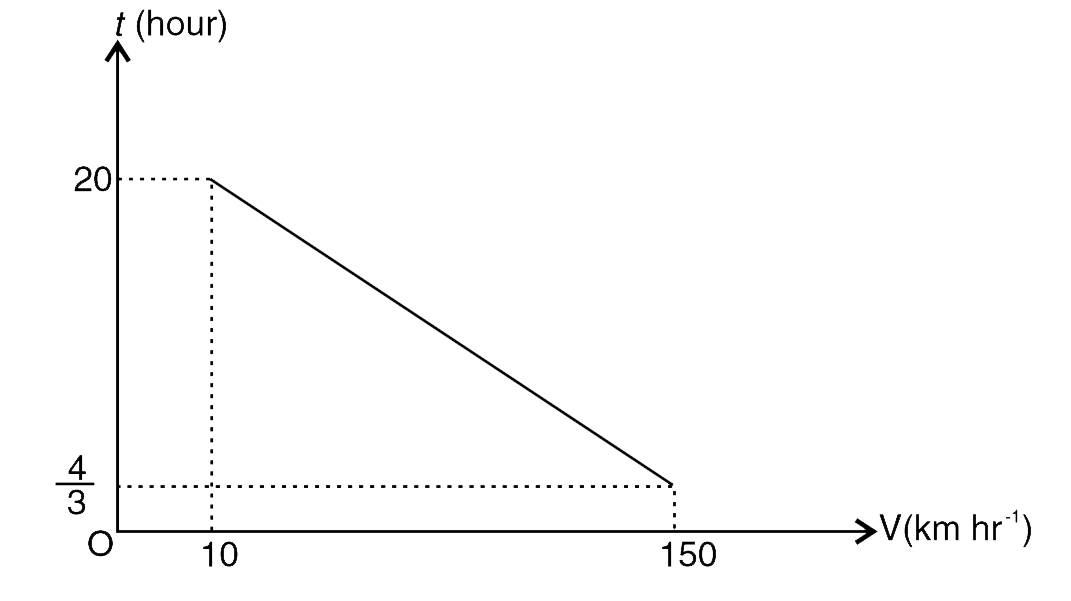
(a) Calculate the optimum speed V0 for this new model.
(b) If the fuel tank capacity of this car is 50 litre, what maximum mileage can be obtained from this car?
View SolutionTwo spherical black bodies of radii R1 and R2 and with surface temperature T1 and T2 respectively radiate the same power. R1/R2 must be equal to
View SolutionA black plane surface at a constant high temperature Th, is parallel to another black plane surface at constant lower temperature Tl. Between the plates is vacuum. In order to reduce the heat flow due to radiation, a heat shield consisting of two thin black plates, thermally isolated from each other, it placed between the warm and the cold surfaces and parallel to these. After some time stationary conditions are obtained. By what factor ≠ta is the stationary heat flow reduced due to the presence of the heat shield? Neglect end effects due to the finite size of the surfaces.
View SolutionThe space between two thin concentric metallic spherical shells of radii a and b is filled with a thermal conducting medium of conductivity k. The inner shell is maintained at temperature T1 and outer is maintained at a lower temperatureT2 . Calculate the rate of flow of heat in radially outward direction through the medium.
View SolutionThe gas between two long coaxial cylindrical surfaces is filled with a homogeneous isotropic substance. The radii of the surfaces are r_(1) = 5.00 cm and r_(2) = 7.00 cm . In the steady state the temperatures of the inner and outer surfaces are T_(1) =290 K and =320 K respectively. Find the temperature of a coaxial surface of radius r.
View Solutionऊष्माक्षेपी अभिक्रिया के लिए तापमान T1 एवं T2 पर साम्यावस्था स्थिरांक क्रमशः Kp और K'p हैं, यदि यह मान लिया जाए कि तापमान सीमा T1 एवं T2 के बीच अभिक्रिया की ऊष्मा स्थिर है | तो आसानी से प्रेक्षित है
View SolutionFigure shows a system of two concentric spheres of radii r_(1)" and "r_(2) at the temperatures T_(1)" and "T_(2) , respectively. The radial rate of flow of heat in a substance filled between the two concentric spheres is proportional to
View SolutionTwo spherical black bodies of radii r1 and r2 and with surface temperatures T1 and T2 respectively, radiate the same power. Then r1/r2 must be equal to
View SolutionA slab of material has area A, thickness L, and thermal conducitivy k. One of its surface (P ) is maintained at temperature T1 and the other surface (Q ) is maintained at a lower temperature T2. The rate of heat flow from P to Q is :
View SolutionHeating of the ends of a cylindrical rod T_(1) and T_(2) Huh. Heat flow rate Q_(1)cal//s is. If all the linear dimensions of the rod are doubled and the temperature is fixed, then the rate of heat flow Q_(2) Will be
View SolutionThe temperature coefficient of a reaction is 2.5 . If its rate constant at T1K is 2.5×10−3s−1, the rate constant at T2K in s−1 is (T2>T1)
View SolutionThe temperature coefficient of a reaction is 2.5. If its rate constant at T1K is 2.5×10−3s−1, the rate constant at T2K in s−1 is (T2=10+T1)
View SolutionThe temperature coefficient of a reaction is 2.5 . If its rate constant at T_(1)K is 2.5xx10^(-3)s^(-1) , the rate constant at T_(2)K in s^(-1) is (T_(2)gtT_(1))
View SolutionA spherical shell of inner radius R1 and outer radius R2 is having variable thermal conductivity given by K=a0T×r, where a0 is constant and T is temperature in kelvin and r is the distance from the centre. Two surface of the shell are maintained at temperature T1 (inner surface) and T2 (outer surface), respectively (T1>T2). The heat current flowing through the shell would be
View Solution

