In the above example, if temperature of inner surface P is kept constant at θ1 and of the outer surface Q at θ2(<θ1). Then,
Find.
(a) rate of heat flow or heat current from inner surface to outer surface.
(b) temperature θ at a distance r(a<r<b) from centre.
The correct Answer is:A, B, D
(a) 
HordQdt=Temperature differenceThermal resistance
=(θ1−θ2)(4πK)1a−1b
=(θ1−θ2)(ab)(4πK)b−a
(b)
In the figure, we can see that
Heat current H1 = Heat current H2
∴((TD)PMRPM)=((TD)MQRMQ) ..........(i)
Using the result obtained in Example-3 of thermal resistance, we can find
RPM=14πK(1a−1r)
and RMQ=14πK(1r−1b)
Substituting the values in Eq. (i), we have
⎛⎜
⎜⎝θ1−θ(14πK)(1a−1r)⎞⎟
⎟⎠=θ−θ2(14πK)(1r−1b)
Solving this equation we can find θ.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Example Type 22videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Example Type 31videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective14videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise13videos
BASIC MATHEMATICS
- BOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
Similar Questions
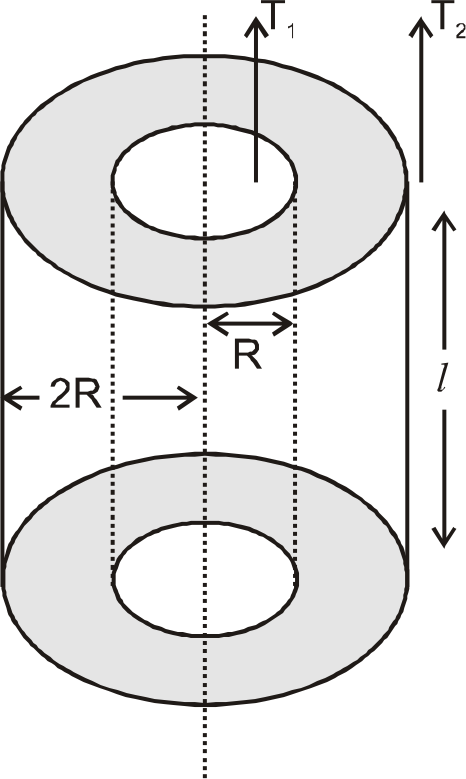
Inner surfaec of a cylindrical shell of length l and of material of thermal conductivity k is kept at constant temperature T1 and outer surface of the cylinder is kept at constant temperature T2 such that (T1>T2) as shown in figure. heat flows from inner surface to outer surface radially outward. inner and outer radii of the shell are R and 2R resspectively. Due to lack of space this cylinder has to be replaced by a smaller cylinder of length l2 inner and outer radii R4 and R respectively and thermal conductivity of material nk. if rate of radially outward heat flow remains same for same temperatures of inner and outer surface i.e., T1 and T2 then find the value of n.View SolutionA charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius of rasius alpha. (a) Find the surface charge density on the inner surface and on the outer surface. (b) If a charge q is pur on the sphege, what would be the surface charge dendities on the inner and the outer surface? (c) Find the electric field inside the sphere at a distance x from the centre in the situations (a) and (b).
View Solution
Knowledge Check
- Question 1 - Select One
If charge q induced on outer surface of sphere of radius R, then intensity at point P at distance S from centre is
Ainversely proportional to (S+R)2Binversely proportional to R2.Cinversely proportional to S2.Ddirectly proportional to S2. - Question 2 - Select One or More
The ends of a metal rod are kept at temperatures θ1 and θ2 with θ2>θ1. The rate of flow of heat along the rod is directly proportional to
Athe length of the rodBthe diameter of the rodCthe cross sectional area of the rodDthe temperature difference (θ2−θ1) between the ends of the rod - Question 3 - Select One
If charge q is induced on outer surface of sphere of radius R, then intensity at a point P at a distance S from its centre is
Ainversely proportional to (S+R)2Binversely proportional to R2Cinversely proportional to S2Ddirectly proportional to S2
A composite spherical shell is made up to two materials having thermal conductivities k and 2k respectively as shown in the diagram . The temperature at the innermost surface is maintained at T whereas the temperature at the outermost surface is maintained at 10 T . A, B, C and D are four points in the outer material such that AB = BC = CD.
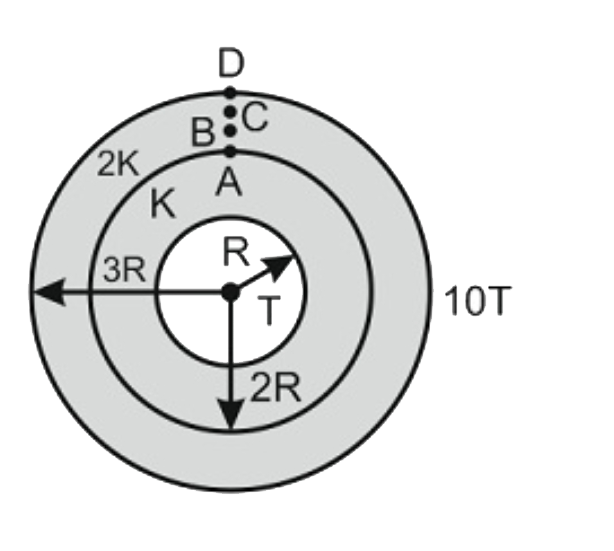
The effective thermal resistance between the inner surface of the shell and the outer surface of the shell for the radial heat flow isView SolutionA stema pipe with a radius R1 is surrounded by an insulating jacket with an outer radius of R0 If the temperature of the inner (θ1) and outer (θ0) surface are fixed (θ1>θ0) find the heat flow through the jacket. (Apply the heat conduction euation to steady state radial heat flow corresponding to cylindrical symmetry) .
View SolutionThe ends of a metal rod are kept at temperature θ1andθ2 with θ2>θ1. At steady state the rate of flow of heat along the rod is directly proportional to
View SolutionInner and outer surfaces of a cylinder are maintained at temperature 4T and T respectively. Heat flows radially from inner surface of radius R to outer surface of radius 4R. Radial distance from the center where temperature is 2T.
View SolutionA slab of material has area A, thickness L, and thermal conducitivy k. One of its surface (P ) is maintained at temperature T1 and the other surface (Q ) is maintained at a lower temperature T2. The rate of heat flow from P to Q is :
View Solution

