The ends of a metal rod are kept at temperature θ1andθ2 with θ2>θ1. At steady state the rate of flow of heat along the rod is directly proportional to
the length of the rod
the diameter of the rod
the cross-sectional area of the rod
the temperature difference (θ2−θ1) between the ends of the rod
The correct Answer is:C, D
Step by step video, text & image solution for The ends of a metal rod are kept at temperature theta_(1) and theta_(2) with theta_(2) gt theta_(1). At steady state the rate of flow of heat along the rod is directly proportional to by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:AAKASH INSTITUTEChapter:THERMAL PROPERTIES OF MATTERExercise:Assignment (Section-D) Linked Comprehension Type Questions
Explore 9 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH INSTITUTEChapter:THERMAL PROPERTIES OF MATTERExercise:Assignment (Section-E) Assertion & Reason Type Question
Explore 10 Videos
- THERMAL PROPERTIES OF MATTERBook:AAKASH INSTITUTEChapter:THERMAL PROPERTIES OF MATTERExercise:Assignment (Section-B) Objective Type questions (one option is correct)
Explore 15 Videos
- TEST 9Book:AAKASH INSTITUTEChapter:TEST 9Exercise:EXAMPLE
Explore 61 Videos
- THERMODYNAMICSBook:AAKASH INSTITUTEChapter:THERMODYNAMICSExercise:ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
Explore 10 Videos
Similar Questions
Calculate θ1 and θ2 in shown situation.
_E01_244_Q01.png)
View SolutionTwo thin metallic spherical shells of radii r1andr2(r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells. Is maintained at temperature θ1 .and the outer shell at temperature θ2(θ1<θ2). Calculate the rate at which heat flows radially through the material.

View Solution
Knowledge Check
The ends of a metal rod are kept at temperatures θ1 and θ2 with θ2>θ1. The rate of flow of heat along the rod is directly proportional to
Athe length of the rodBthe diameter of the rodCthe cross sectional area of the rodDthe temperature difference (θ2−θ1) between the ends of the rodA metal bar of length l is well lagged with some non-conducting material to prevent losses of heat from its surface and the two ends are maintained at steady temperatures θ1 and θ2 with θ1>θ2, then in the steady state the temperature θ of s section of the bar at distance x from the hot end varies as shown in the graph
A B
B C
C D
D
Two different metal rods of the same length have their ends kept at the same temperature θ1, and θ2with θ2>θ1. If A1 and A2 are their cross-sectional areas and K1 and K2 their thermal conductivities, the rate of flow of heat in the two rods will be the same it:
AA1A2=k1k2BA1A2=k2k1CA1A2=k1θ1k2θ2DA1A2=k2θ2k1θ1
Three rods AB,BCand BD having thremal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in The ends A,C and D are at temperature θ1,θ2 and θ3 respectively Find the temperature of the junction B
(Assume steady state and θ1>θ>θ2>θ3)
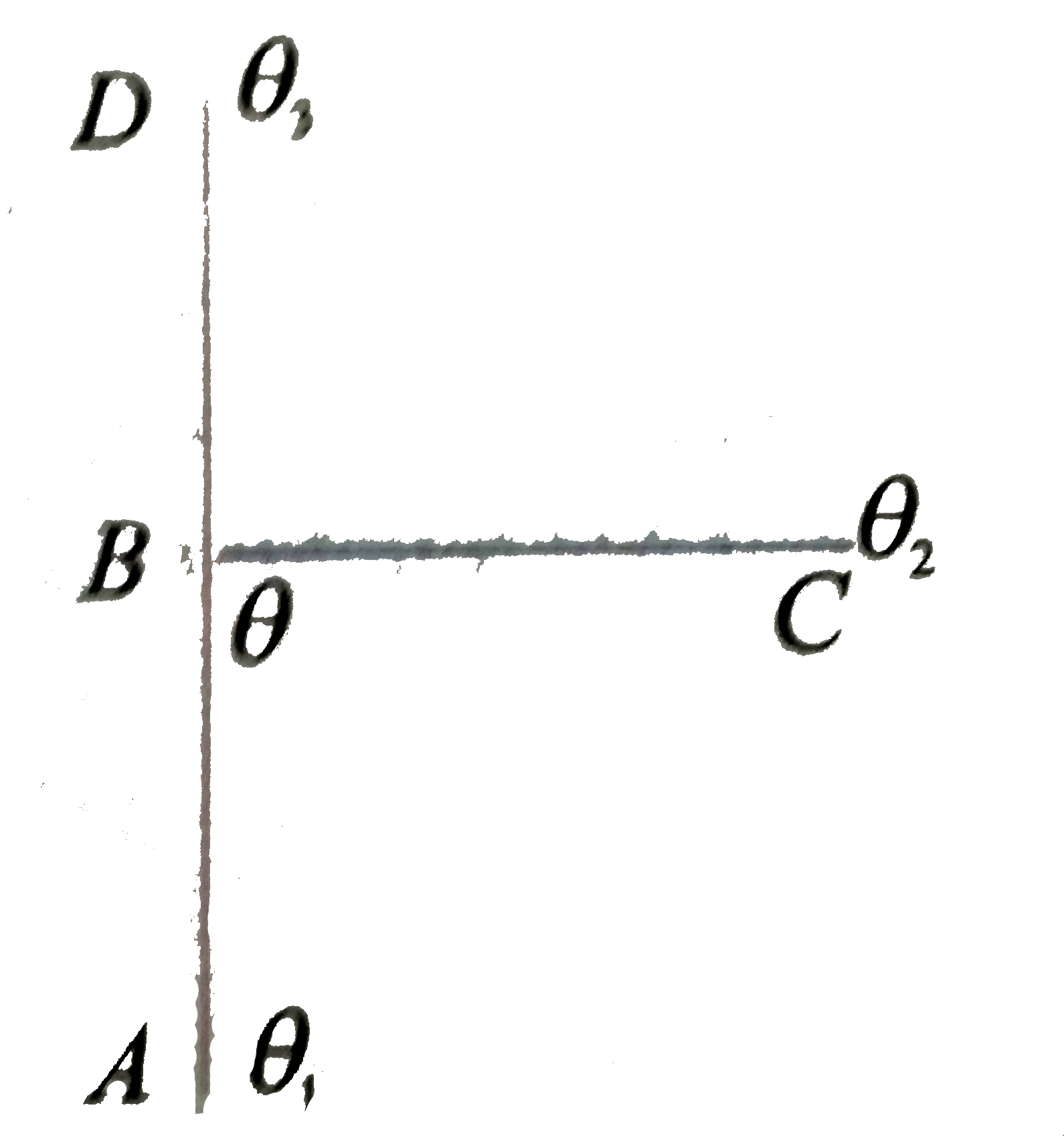 .
.
View SolutionA stema pipe with a radius R1 is surrounded by an insulating jacket with an outer radius of R0 If the temperature of the inner (θ1) and outer (θ0) surface are fixed (θ1>θ0) find the heat flow through the jacket. (Apply the heat conduction euation to steady state radial heat flow corresponding to cylindrical symmetry) .
View Solutionif tanθ1=kcotθ2 then find cos(θ1−θ2)cos(θ1+θ2)=
View SolutionOne end of a metal rod is kept in a furnce. In steady state, the temperature of the rod
View SolutionIf tanθ1.tanθ2=k, then: (cos(θ1−θ2)cos(θ1+θ2)=
View Solution

