A spherical body of radius 'b' has a concentric cavity of radius 'a' as shown. Thermal conductivity of the material is K. Find thermal resistance between inner surface P and outer surface Q.
The correct Answer is:A, B, D
As we move from P to Q surface perpendicular to PQ is spherical and its size keeps on increasing (just like different layers of a spherical onion). So, first we will calculate thermal
resistance of one layer at a distance r from centre and thickness dr by using the formula
R=lKA
In this formula, dimension of the layer along PQ is dr and the surface area perpendicular to PQ
is 4πr2
∴dR=drK(4πr2)
Now, if we integrate dR from r = a to r= b, we will get the total thermal resistance between P
and Q. Thus,
R=∫badR=∫badrK(4πr2)
Solving this expression, we get
R=14πK(1a−1b).
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Example Type 22videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Example Type 31videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective14videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise13videos
BASIC MATHEMATICS
- BOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
Similar Questions
Thermal conductivity of the conductor shown in figure is K. Find thermal resistance between points a and b.
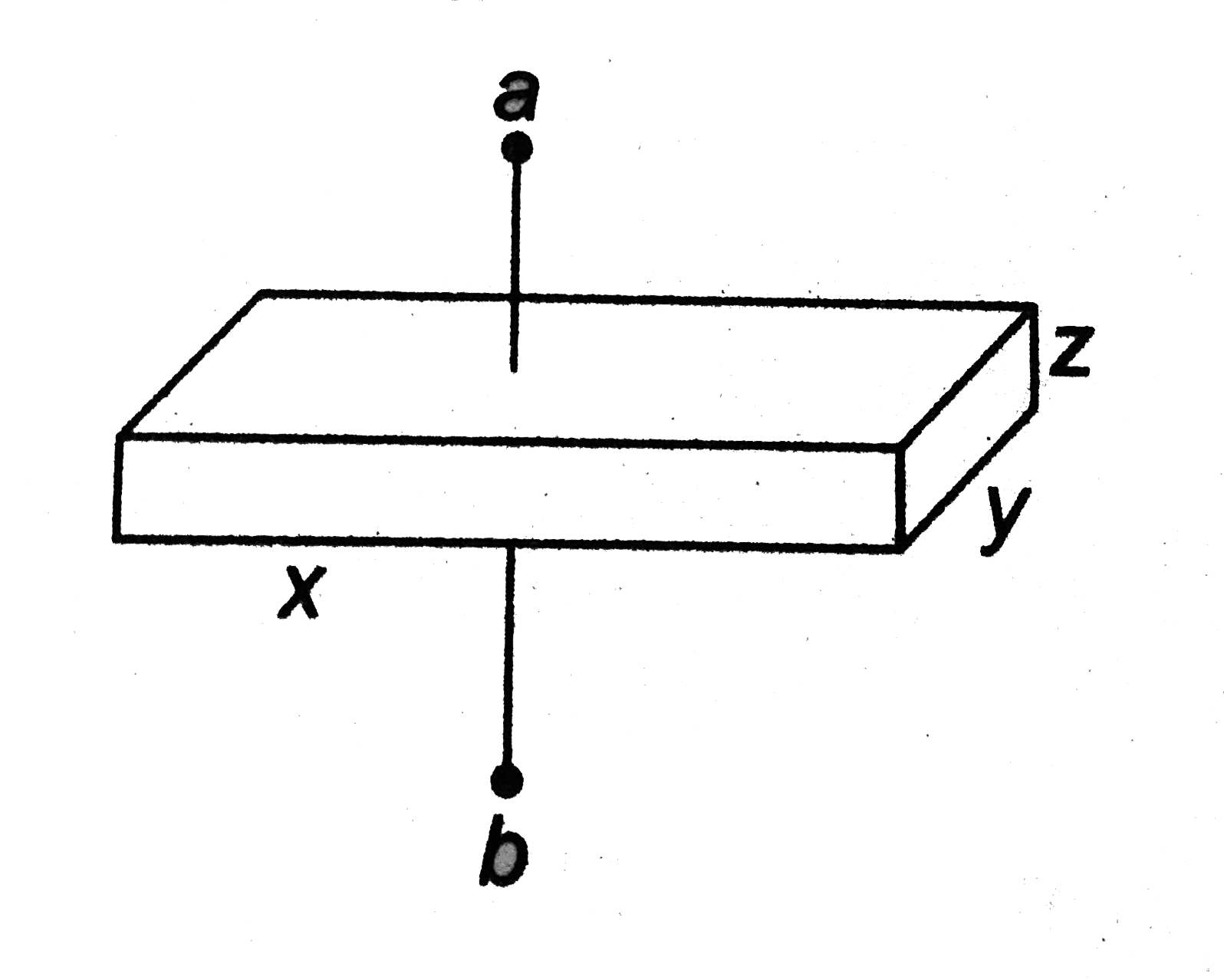. View SolutionA solid spherical conductor of radius R has a spherical cavity of radius a(a+Q is kept at the center.The charge at the inner surface outer and at a position r(a<r<R)are respectively.
View Solution
Knowledge Check
- Question 1 - Select One
A metallic sphere having inner and outer radii a and b respectively has thermal conductivity
K=K0r(a≤r≤b)
Find the thermal resistance between inner surface and outer surface.A(b−a)4πK0B(b2−a2)4πKaabC4πK0(b−a)Dnone of these - Question 2 - Select One
A solid spherical conductor of radius R has a spherical cavity of radius at its centre. A charge is kept at the centre of the cavity. The charge at the inner surface, outer surface are respectively.
A+Q,−QB−Q,+QCQ,−QD+Q,0 - Question 3 - Select One
Space between tow concentric spheres of radii r1andr2 such that r1<r2 is filled with a material of resistivity ρ. Find the resistance between inner and outer surface of the material
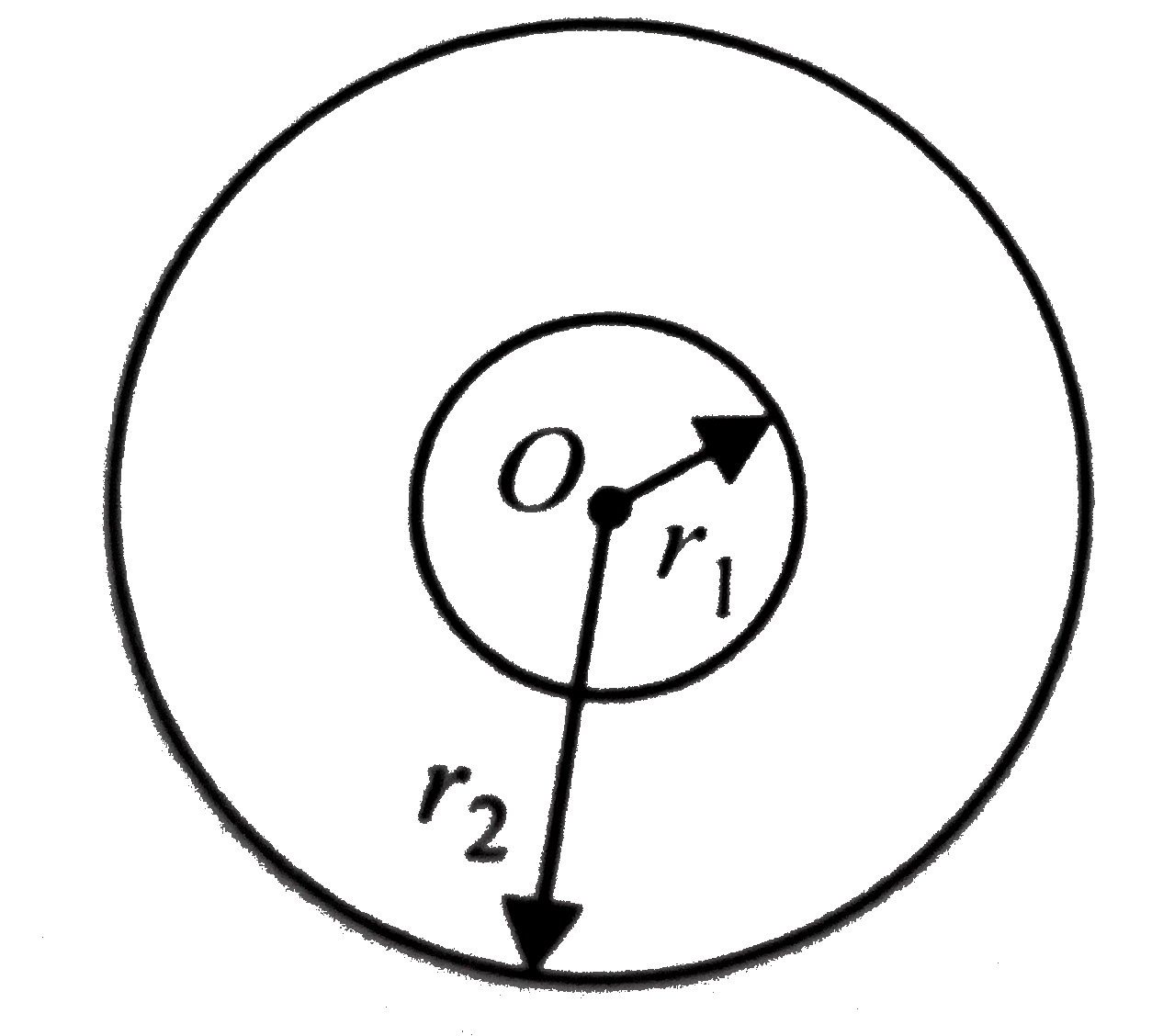Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these.
What is the volume of the material in a spherical shell with inner radius ‘r' and outer radius 'R' ?
View SolutionA solid sphere of radius R has a concentric cavity of radius R3 inside it. The sphere is found to just float in water with the highest point of it touching the water surface. Find the specific gravity of the material of the sphere.
View SolutionA point source of heat of power P is placed at the centre of a spherical shell of mean radius R. The material of the shell has thermal conductivity K. If the temperature difference between the outer and inner surface of the shell in not to exceed T, the thickness of the shell should not be less than .......
View SolutionA cylinder of radius R is surrounded by a cylindrical shell of inner radius R and oputer radius 2R. The thermal conductivity of the material of the inner cylinder si k1 and that of the outer cylinder is K2 ,Assumming no loss of heat , the effective thermal conductivity of the system for heat flowing along the length of the cylionder is :
View SolutionSphere of inner radius a and outer radius b is made of p uniform resistivity find resistance between inner and outer surface
View Solution