A steel wire is rigidly fixed at both ends its length mass and cross sectional area are 1m, 0.1 kg and 106m2 respectively then the temperature of the wire is lowered by 20∘C if the transverse waves are setup by plucking the wire at 0.25m from one end and assuming that wire vibrates with minimum number of loops possible for such a case. Find the frequency of vibration (in Hz). [coefficient of linear expansion of steel =1.21×10−6/.∘C and young's modulus =2×1011/N/m2]
The mechanical strain =△ll=α△T=1.21×10−5×20=2.42×10−5
The tension in wire =T=Y△llA=2×1011×2.42×10−5×10−6=48.4N
∴ speed of wave in wire
V=√Tμ=√48.40.1=22m/s
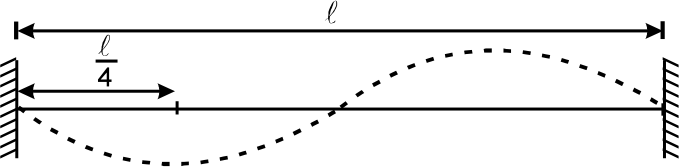
Since the wire is plucked at l4 from one end the wire shall oscillate in 1st overtone (for minimum number of loops)
λ=l=1m
Now V=fλ or f=Vλ=22Hz
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased then
View SolutionA steel wire of length 1m , mass 0.1kg and uniform cross-sectional area 10^(-6)m^(2) is rigidly fixed at both ends. The temperature of the wire is lowered by 20^(@)C . If transverse calculate the frequency of the fundamental mode of vibration. Given for steel Y = 2 xx 10^(11)N//m^(2) alpha = 1.21 xx 10^(-5) per ^(@)C
View SolutionOne end of a uniform wire of length 'L' and mass 'M' is attached rigidly to a point in the roof and a load of a mass 'm' is suspended from its lower end. If A is the area of cross-section of the wire then the stress in the wire at height 'x' from its lower end (x lt L) is
View SolutionA steel wire of length 1 m and mass 0.1 kg and having a uniform cross-sectional area of 10^(-6) m^(2) is rigidly fixed at both ends. The temperature of the wire is lowered by 20^(@)C . If the wire is vibrating in fundamental mode, find the frequency (in Hz). (Y_(steel)=2xx 10^(11) N//m^(2),alpha_(steel)=1.21 xx 10^(-5)//.^(@)C) .
View SolutionA steel wire is rigidly fixed at both ends. Its length mass and cross-sectionl area are 1m, 0.1kg and 10−8m2 respectively. Tension in the wire is produced by lowering the temperature by 20∘C. If the transerverse waves are some up by plucking the wire at 0.25m from one end and assuming that the wire viberates with minimum number of loops possble for such a case. The frequency of viberation (in Hz) is found to be. 1.11. Find the value of K. Given α=1.21×10−5.∘C−1.Y−2×1011N/m2

View Solutionएक 4 मीटर लम्बा तार अपने सिरे पर लगे 300 हट्स के कम्पित्र के द्रारा कम्पनशील है। तार चार खण्डों में कम्पन कर रहा है। तार में अनुप्रस्थ तरंगो की चाल है :
View Solutionचित्र में दिखाई गई घिरनियों के बीच तार की लंबाई 1.5m है तथा इसका द्रव्यमान 12.0g है। यदि इस तार को दो लूपों में कंपित कराया जाए, तो उसकी कंपन आवृत्ति क्या होगी ।

View SolutionIn a stretched wire under tension and fixed at both ends, the area of cross section of the wire is halved and the tension is doubled. The frequency of the wire will be
View SolutionA uniform wire of length L and weight W is rigidly fixed at one end and a load W_1 is applied at its othe end. IF the area of cross section of the wire is S, then stress developed In the wire at a distance (3L)/4 from its lower end will be (assume that increase in length of the wire is very small)
View SolutionA steel wire of length 1 m, mass 0.1 kg and uniform cross sectional area 10^(-6)m^(2) is rigidly fixed at two ends. The temperature of the wire is lowered by 20^(@) C . If transverse waves are now set up by lucking the string at the middle, calculate the frequency of the fundamental tone. Givne, for steel, co-efficient of linear expansion = 1.21 xx 10^(-5_(@))C^(1) and Young's modulus = 2 xx 10 ^(11) N* m^(-2) .
View SolutionA sonometer wire of length L is plucked at a distance L//8 from one end then it vibrates with a minimum frequency n . If the same wire plucked at a distance L//6 from another end the minimum frequency with which it vibrates is
View SolutionA steel wire of length lm, mass 0.1 kg and uniform cross-sectional area 10−6m2 is rigidly fixed at both ends. The temperature of the wire is lowered by 200C. If the transverse waves are set up by plucking the string in the middle, calculate the frequency of the fundamental mode of vibration [Y=2×1011N/m2andα=1.21×10−5l0C]
View SolutionOne end of a uniform wire of length .L. and mass .M. is attached rigidly to a point in the roof and a load of mass .m. is suspended from its lower end. If A is the area of corss - section of the wire then find the stress in the wire at height .x. from its lower end (x<L)
View SolutionA steel wire of length lm, mass 0.1 kg and uniform cross-sectional area 10^(-6)m^(2) is rigidly fixed at both ends. The temperature of the wire is lowered by 20^(0)C . If the transverse waves are set up by plucking the string in the middle, calculate the frequency of the fundamental mode of vibration [Y=2xx10^(11)N//m^(2) and alpha=1.21xx10^(-5)l^(0)C]
View Solution

