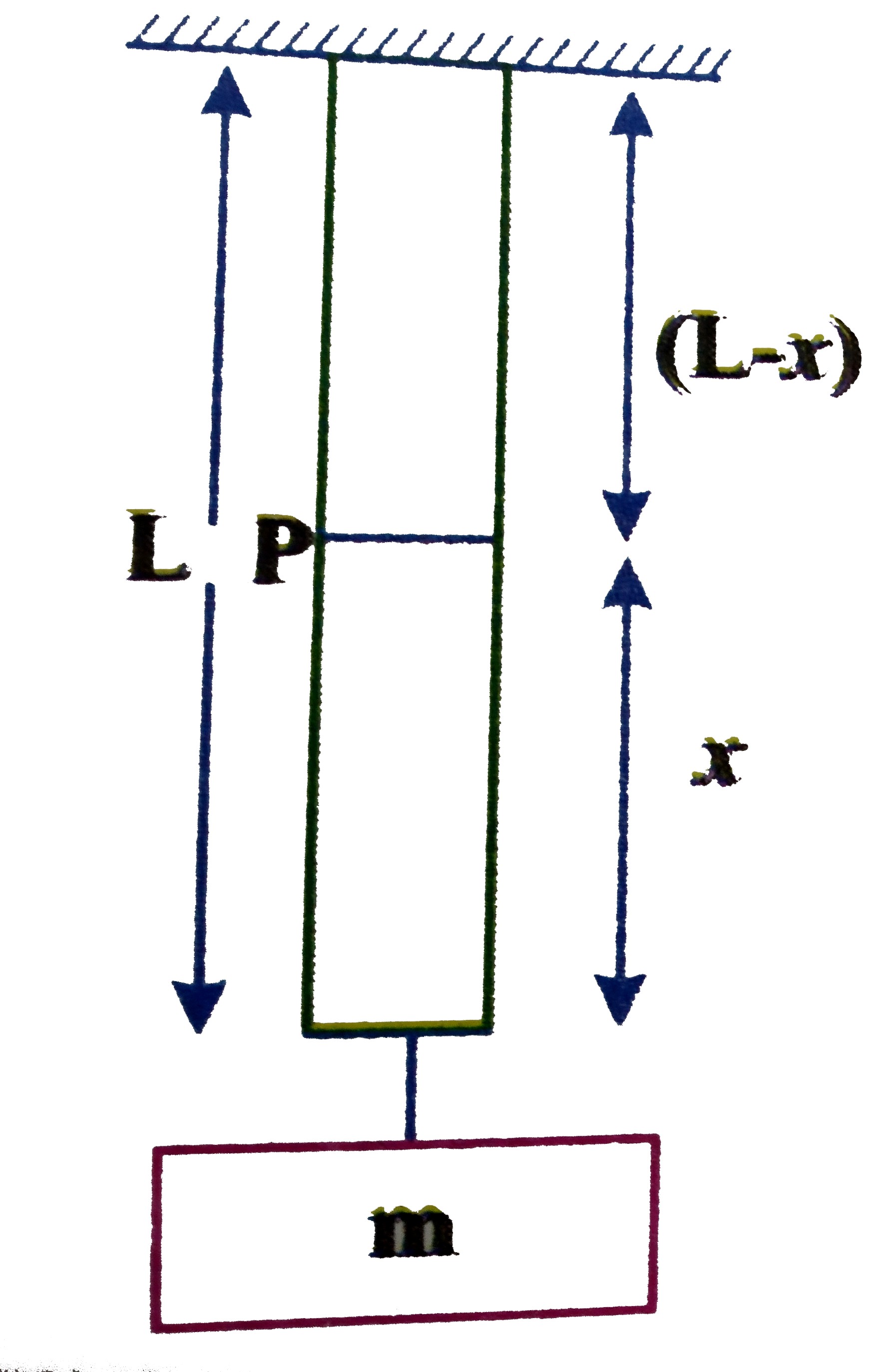
One end of a uniform wire of length and mass is attached rigidly to a point in the roof and a load of a mass is suspended from its lower end. If is the area of cross-section of the wire then the stress in the wire at height from its lower end is
The correct Answer is:C
Tension in the string at point is
of load of wire of length
, Stress at
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-III
Explore 29 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:NCERT BASED QUESTIONS
Explore 21 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-I (C.W)
Explore 37 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:EXERCISE - III
Explore 30 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-II(H.W)
Explore 31 Videos
Similar Questions
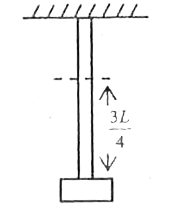
One end of a uniform wire of length L and of weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If S is the area of cross-section of the wire, the stress in the wire at a height 3 L/4 from its lower end is
View SolutionOne end of a uniform wire of length L and weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If S is the area of cross section of the wire, the stress in the wire at a height (3L/4) from its lower end is
View Solution
Knowledge Check
One end of a unifrom wire of length L and weigth W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If S is the area of cross-section of the wire then the stress in the wire at a height 3L4 from its lower end is
A(W1+W)SBW1SC(W1+3W4)SD(W1+W4)SOne end of uniform wire of length L and of weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If s is the area of cross section of the wire, the stress in the wire at a height (3L/4) from its lower end is
AW1ABW1+(W/4)ACW1+(3W/4)ADW1+WAOne end of uniform wire of length L and of weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If s is the area of cross section of the wire, the stress in the wire at a height (3L/4) from its lower end is
AW1sB[W1+W4]sC[W1+3W4]/sDW1+Ws
One end of uniform wire of length L and of weight W is attached rigidly to a point in the roof and a weight N is suspended from its lower end if s is the area of cross-section of the wire the stress in the wire at a height L4 from its lower end is
View SolutionOne end of a wire of length L and weight w is attached rigidly to a point in roof and a weight w1 is suspended from its lower end. If A is the area of cross-section of the wire then the stress in the wire at a height 3L4 from its lower end is
View SolutionOne end of uniform wire of length Land of weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If S is the area if cross-section of the wire, the stress in the wire at a height (3L/4) from its lower end is
View SolutionOne end of a uniform wire of length l and weight W is attached to a point in the roof and a weight W/2 is suspended from the lower end. If A is the area fo cross-section of the wire, then stress of the wire at its midpoint will be
View SolutionOne end of uniform wire of length L and of weight W is attached rigidly to a point in the roof and a weight W1 is suspended from its lower end. If s is the area of cross section of the wire, the stress in the wire at a height (3L/4) from its lower end is
View Solution

