A rod of length $l$ with thermally insulated lateral surface is made of a material whose thermal conductivity varies as $K = s c / T$ where $c$ is a constant. The ends are kept at temperatures $T_{1}$ and $T_{2}$ . Find the temperature at a distance $x$ from te first end where the temperature is $T_{1}$ and the heat flow density.

Video Solution

Text Solution

Verified by Experts

Given $K = \frac{C}{T}$

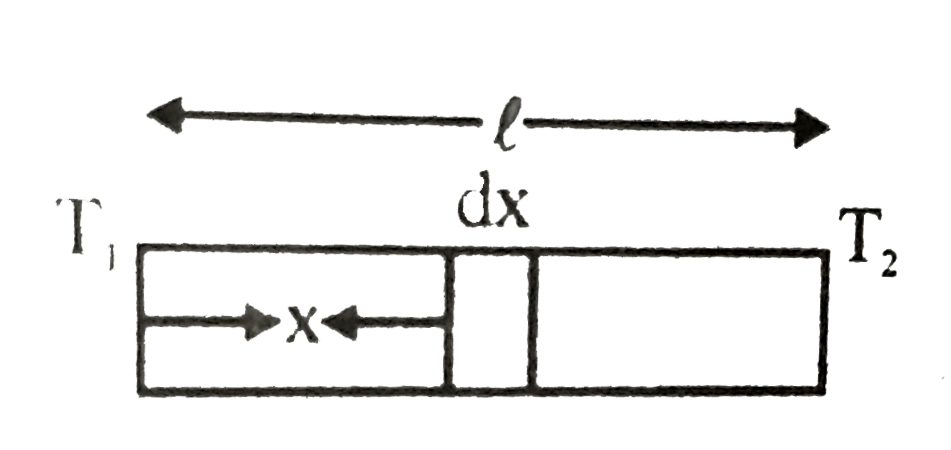
Consider an element of length $' d x'$ at a distance of $' x'$ from the end having temperature $T_{1}$
Consider temperature at one end of the element to be $' T'$ and at after end to be $' T + d T'$ Then
$\frac{d H}{d t} = i \frac{k A d T}{d x}$ $[K = \frac{C}{T}]$
$\Rightarrow i = \frac{- C}{T} = \frac{A d T}{d x}$
$\int_{0}^{x} i d x = - \int_{T_{1}}^{T} \frac{C A d T}{T}$
$i x = - C A in (\frac{T}{T_{1}}$ .......... $(i)$
$\int_{0}^{l} i d x = - \int_{T_{1}}^{T_{2}} \frac{C A d T}{T}$
$i l = - C A in (\frac{T_{2}}{T_{1}})$ ...... $(i i)$
divide $(i)$ with $(i i)$ given
$\frac{x}{l} = \frac{in (\frac{T}{T_{1}})}{I n (\frac{T_{2}}{T_{1}})}$
${(\frac{T_{2}}{T_{1}})}^{x / l} = \frac{T}{T_{1}} \Rightarrow T = T_{1} {(\frac{T_{2}}{T_{1}})}^{x / l}$
Heat flow (rate) $i = K A \frac{d T}{d x} = \frac{C}{l} \times A \times \frac{T}{l} ln (\frac{T_{1}}{T_{2}}) = \frac{C A}{l} ln (\frac{T_{1}}{T_{2}})$
Current density $= \frac{i}{A} = \frac{C}{l} ∣ ∣ ∣ ln (\frac{T_{1}}{T_{2}}) ∣ ∣ ∣$

Updated on:21/07/2023

Class 11 PHYSICS THERMAL EXPANSION AND CALORIMETRY

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A rod of length l (laterally thermally insulated) of the uniform cross sectional area A consists of a material whose thermal conductivity varies with temperature as $K = \frac{K_{0}}{a + b T'}$ where $K_{0}$ , a and b are constants. $T_{1}$ and $T_{2} (< T_{1})$ are the temperatures of the ends of the rod. Then, the rate of flow of heat across the rod is
A $\frac{A K_{0}}{b l} (\frac{a + b T_{1}}{a + b T_{2}})$
B $\frac{A K_{0}}{b l} (\frac{a + b T_{2}}{a + b T_{1}})$
C $\frac{K_{0} A}{b l} ln [\frac{a + b T_{1}}{a + b T_{2}}]$
D $\frac{A K_{0}}{b l} ln [\frac{a + b T_{2}}{a + b T_{1}}]$
Question 2 - Select One
Two walls of thickness d and d and thermal conductivities k and k are in contact. In the steady state, if the temperature at the outer $T_{1}$ and $T_{2}$ , the temperature at the common wall is
A $\frac{k_{1} T_{1} d_{2} + k_{2} T_{2} d_{1}}{k_{1} d_{2} + k_{2} d_{1}}$
B $\frac{k_{1} T_{1} + k_{2} d_{2}}{d_{1} + d_{2}}$
C $(\frac{k_{1} d_{1} + k_{2} d_{2}}{T_{1} + T_{2}}) T_{1} T_{2}$
D $\frac{k_{1} d_{1} T_{1} + k_{2} d_{2} T_{2}}{k_{1} d_{1} + k_{2} d_{2}}$
Question 3 - Select One
Two identical rods are made of different materials whose thermal conductivities are $K_{1} and K_{2}$ . They are placed end to end between two heat reservoirs at temperatures $θ_{1} and θ_{2}$ . The temperature of the junction of the rod is

A $\frac{θ_{1} + θ_{2}}{2}$
B $\frac{K_{1} θ_{1} + K_{2} θ_{2}}{K_{1} + K_{2}}$
C $\frac{K_{1} θ_{2} + K_{2} θ_{1}}{K_{1} + K_{2}}$
D $\frac{K_{1} θ_{1} + K_{2} θ_{2}}{[K_{1} - K_{2}]}$

BANSAL-HEAT TRANSFER-Exercise

Home
Ask Doubt
Profile

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two walls of thickness d and d and thermal conductivities k and k are in contact. In the steady state, if the temperature at the outer T1 and T2 , the temperature at the common wall is

Two identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

BANSAL-HEAT TRANSFER-Exercise

Two walls of thickness d and d and thermal conductivities k and k are in contact. In the steady state, if the temperature at the outer $T_{1}$ and $T_{2}$ , the temperature at the common wall is

Two identical rods are made of different materials whose thermal conductivities are $K_{1} and K_{2}$ . They are placed end to end between two heat reservoirs at temperatures $θ_{1} and θ_{2}$ . The temperature of the junction of the rod is