Hot oil is circulated thorugh an insulated container with a wooden lid at the top whose conductivity K=0.149J/(m−∘C−sec), thickness t=5mm,emissivity=0.6 Temperature of the top of the lid is maintaining at Tl=127∘C. If the ambient temperature Ta=27∘C.
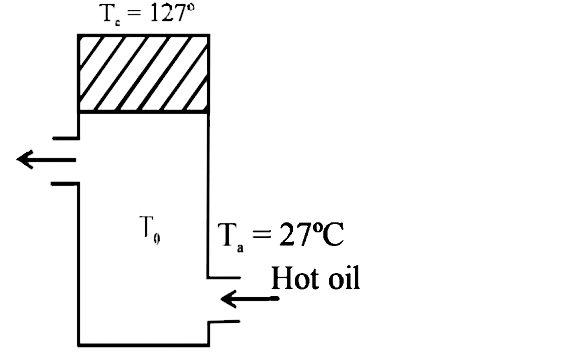
Calculate:
(a) rate of heat loss per unit area due to radiation from the lid.
(b) temperature of the oil. (Givenσ=173×10−8Wm−2K−4)
(a) The rate of heat loss per unit area per second due to radiation is given by stefan's Boltazmann law
E=εσ(T4−T40)
=0.6×173×10−8[(4004)−(300)4]
=595Watt/m2
(b) Let Toil be the temperture of the oil.
Then rate of heat flow through conduction = Rate of heat flow through radiation
KA(Toil−T)l=595×A
Where A is the area of the top of lid
⇒Toil595×ll+T=595×5×10−30.149+400=419.83K
Topper's Solved these Questions
Similar Questions
An insulated container has a wooden lid at the top whose conductivity is 0.15J/m∘Cs , thickness is 5 mm and emissivity is 0.5. The temperature of the top of the wooden lid is maintained at 125∘C and the ambient temperature is 27∘C . Hot liquid is now circulated through the container as shown in the figure. Determine the rate of loss of heat per unit area due to radiation from the wooden lid and temperature of the oil.

Take σ=5.66×10−8Wm−2K−4
View SolutionA metallic ball of surface area 300cm2 at a temperature of 227∘C is placed in a container at 27∘C . Calculate the rate of loss of heat radiation by the ball if emissivity of ball is 0.3, σ=5.67×10−5ergcm−2s−1K−4 .
View Solution
Knowledge Check
The radiant power of a furnace of surface area of 0.6m2 is 34.2KW The temperature of the furance s [σ=5.7×10−8Wm−2K−4 .
A3400KB1012KC1000KD5700KA body at a temperature of 727∘C and having surface area 5cm2, radiations 300J of energy each minute. The emissivity is(Given Boltzmann constant =5.67×10−8Wm−2K−4
Ae=0.18Be=0.02Ce=0.2De=0.15A metal ball of surface area 200cm2 and temperature 527∘C is surrounded by a vessel at 27∘C . If the emissivity of the metal is 0.4, then the rate of loss of heat from the ball is (σ=5.67×10−8J/m2−s−k4)
A108WB168WC182WD192W
A sphere of radius 15 cm is at a temperature of 215∘C . Find the maximum amount of heat which may be lost per second by radiation when the sphere is placed in an enclosure at 25∘C. Take, σ=5.67×10−8Wm−2K4
View SolutionA rod of length L with sides fully insulated is made of a material whose thermal conductivity K varies with temperature as K=αT where α is constant. The ends of rod are at temperature T1 and T2(T2>T1) Find the rate of heat flow per unit area of rod .
View SolutionAssume that the total surface area of a human body is 1−6m2 and that it radiates like an ideal radiator. Calculate the amount of energy radiates per second by the body if the body temperature is 37∘C . Stefan constant σ is 6.0×10−sWm−2K−4 .
View SolutionA black ened metal sphere of radius 7 cm is encllosed in as evacuated chamber maintained at a temperature of 27∘C. At what rate must energy be supplied to the sphere so as to keep its temperature constant at 127∘C ?
σ=5.7×10−8Wm−2K−4.
View SolutionCalculate the energy radiated in one minute by a blackbody of surface area 200 cm2 at 127 ∘C(σ=5.7×10−8Jm−2s−1K−4)
View Solution
