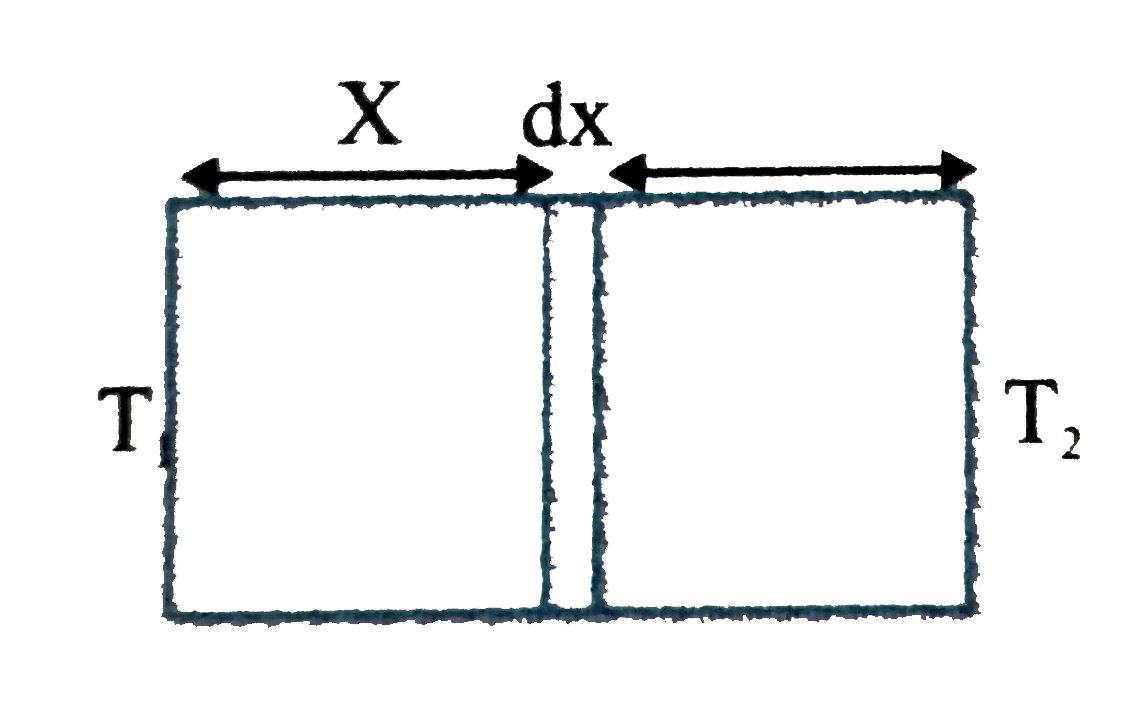
A rod of length l with thermally insulated lateral surface is made of a matrical whose thermal conductivity varies as $K = C / T$ where $C$ is a constant The ends are kept at temperature $T_{1}$ and $T_{2}$ The temperature at a distance x from the first end where the temperature is $T_{1}, T = T_{1} {(\frac{T_{2}}{T_{1}})}^{n x / 2 l}$ Find the value of n? .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Two walls of thickness d and d and thermal conductivities k and k are in contact. In the steady state, if the temperature at the outer $T_{1}$ and $T_{2}$ , the temperature at the common wall is
A $\frac{k_{1} T_{1} d_{2} + k_{2} T_{2} d_{1}}{k_{1} d_{2} + k_{2} d_{1}}$
B $\frac{k_{1} T_{1} + k_{2} d_{2}}{d_{1} + d_{2}}$
C $(\frac{k_{1} d_{1} + k_{2} d_{2}}{T_{1} + T_{2}}) T_{1} T_{2}$
D $\frac{k_{1} d_{1} T_{1} + k_{2} d_{2} T_{2}}{k_{1} d_{1} + k_{2} d_{2}}$
If two bodies at different temperatures $T_{1}$ and $T_{2}$ are brought in thermal contact, the mean temperature $\frac{T_{1} + T_{2}}{2}$ . When
Amass of two bodies are equal
Bpressure on two bodies are equal
Ctherma capacities of two bodies are equal
Dvolume of two bodies are equal
A rod of length l (laterally thermally insulated) of the uniform cross sectional area A consists of a material whose thermal conductivity varies with temperature as $K = \frac{K_{0}}{a + b T'}$ where $K_{0}$ , a and b are constants. $T_{1}$ and $T_{2} (< T_{1})$ are the temperatures of the ends of the rod. Then, the rate of flow of heat across the rod is
A $\frac{A K_{0}}{b l} (\frac{a + b T_{1}}{a + b T_{2}})$
B $\frac{A K_{0}}{b l} (\frac{a + b T_{2}}{a + b T_{1}})$
C $\frac{K_{0} A}{b l} ln [\frac{a + b T_{1}}{a + b T_{2}}]$
D $\frac{A K_{0}}{b l} ln [\frac{a + b T_{2}}{a + b T_{1}}]$