In the fig the pulled has a mass M, radius r and the string does not slip over it. The time period of oscillation is
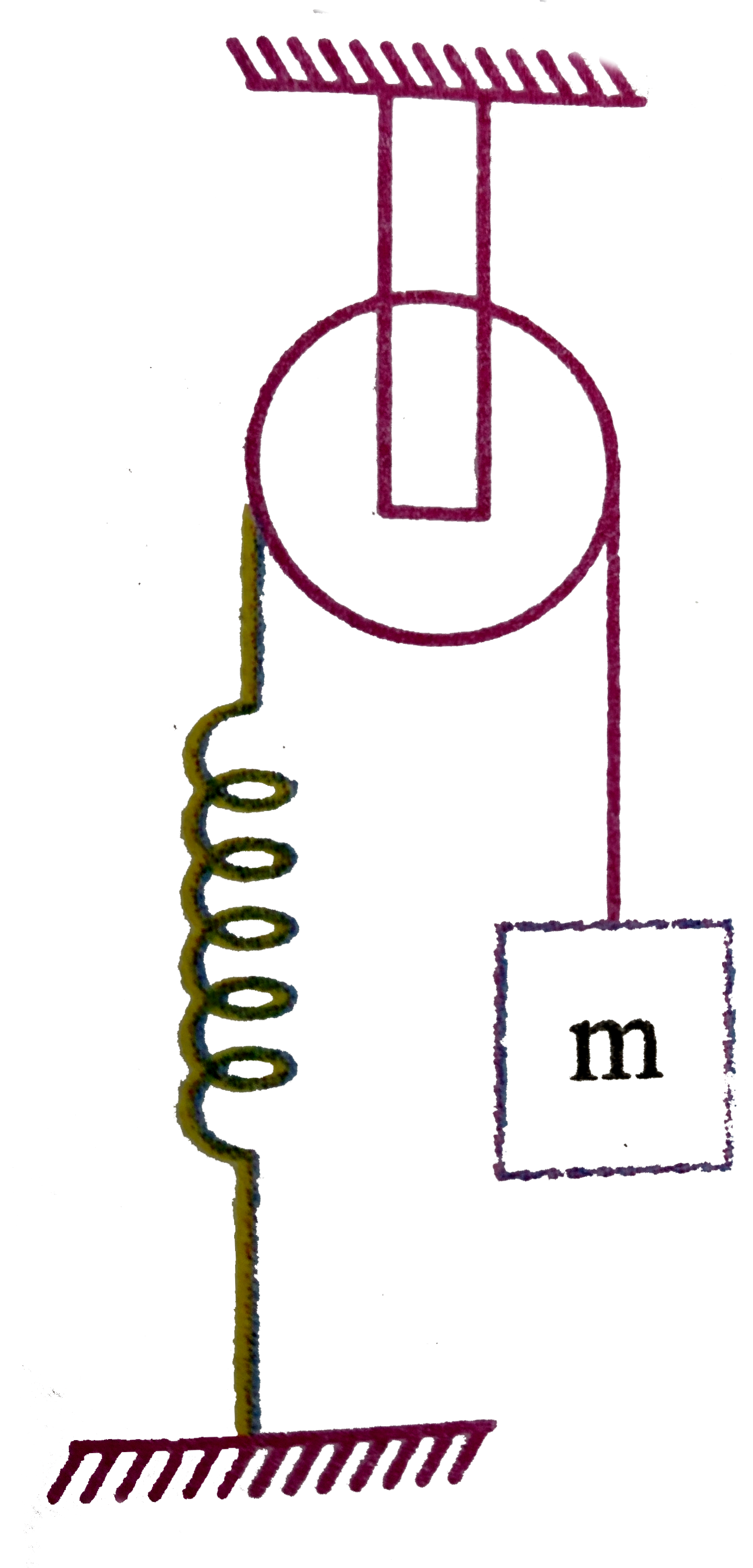
2π√2m+M2k
2πR√2m+3MR22k
2π√mk
2π√m+Mk
The correct Answer is:A
from energy method 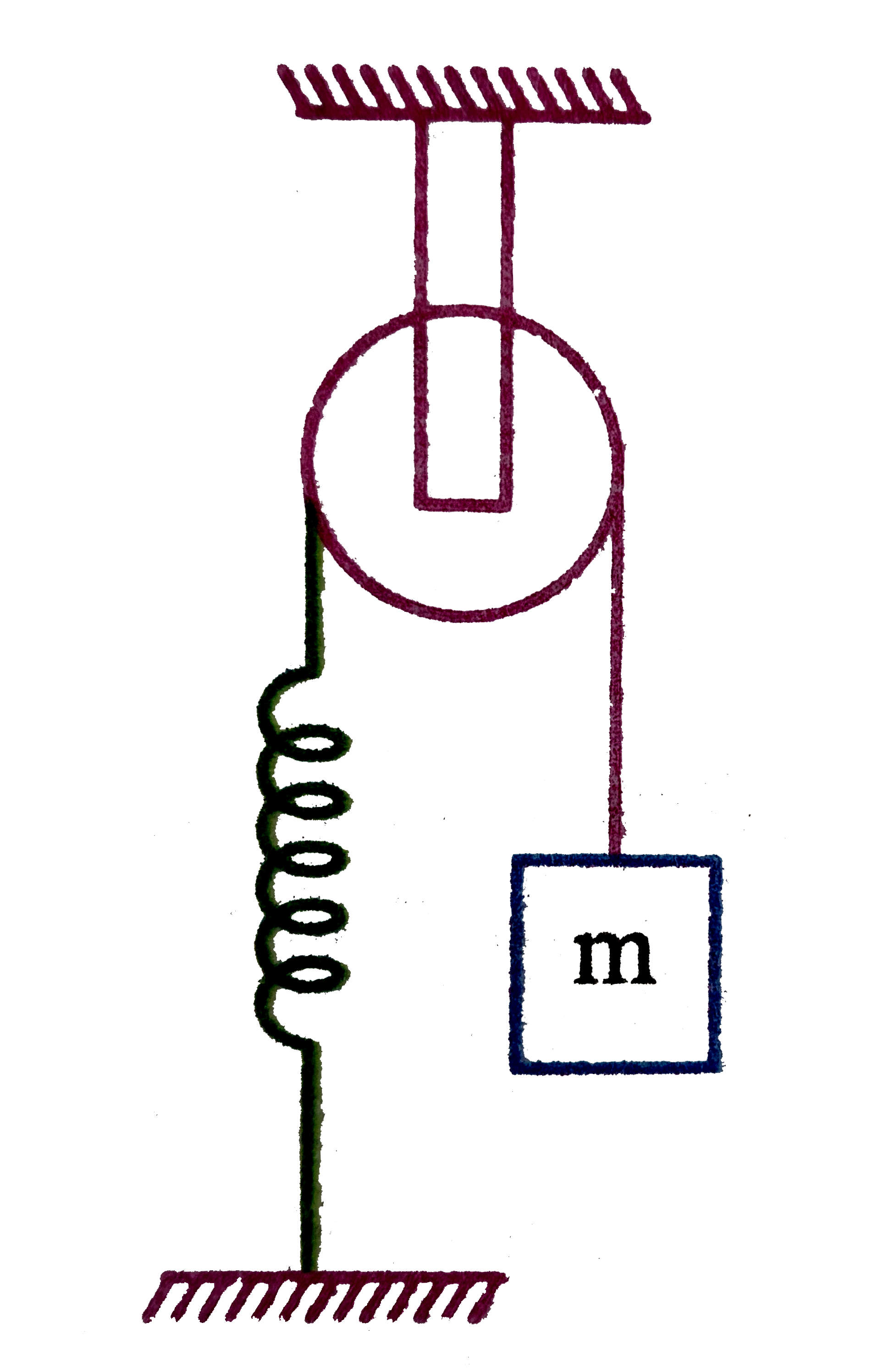
E=12mv2+12Iω2+12k[(x+δ)2−δ2]−mgx
=constant Where I=MR22,δ=mgk= extension in mean position. dEdt=0. Use dvdt=a=ω2x,T=2πω
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage-I
Explore 2 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage
Explore 33 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL-V
Explore 1 Video
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
In the figure, the blocks unequal masses m1 and m2 (m1<m2).m2 has a downward acceleration a. The pulley P has a radius r, and some mass. The string does not slip on the pulley. Find the acceleration of block and angular acceleration of pulley. (I = momentum of inerita of pulley)
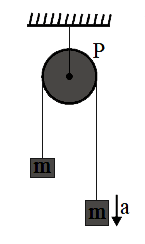
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View Solution
Knowledge Check
The time period of small oscillations of mass m :-
_S01_040_Q01.png) A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A2π√m6kB2π√11m6KC2π√6m11KD2π√mKIn the figure, the disc D does not slip on the surface S, the pulley P has mass and the string does not slip on it. The string is wound around the disc.
 AThe acceleration of the block B is double the acceleration of the centre of DBthe force of friction exerted by D on S acts to the leftCthe horizontal and the vertical sections of the string has the same tensionDthe sum of the kinetic energies of D and B is less than the loss in the potential energy of B as it moves down
AThe acceleration of the block B is double the acceleration of the centre of DBthe force of friction exerted by D on S acts to the leftCthe horizontal and the vertical sections of the string has the same tensionDthe sum of the kinetic energies of D and B is less than the loss in the potential energy of B as it moves downA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
Amg2m+MB2mgm+MCmgm+MD2mg2m+M
A ball of radius r is made to oscillate in a bowl of radius R, find its time period of oscillation.
View SolutionSolve the previous problem if the pulley has a moment of inertia I about its axis and the string does not slip over it.
View SolutionIn the device shown in Fig, the block m is displaced down slightly and released. It starts oscillating. Pulleys are smooth and massless string and springs are also massless. Find time period of oscillations.

View SolutionA mass 'm' is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall or release?
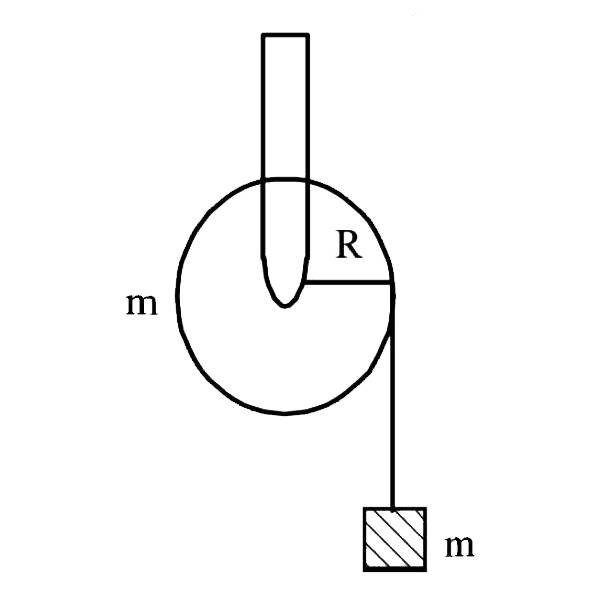
View Solution
A uniform semicurcular ring having mass m and radius r is hanging at one of its ends freely as shown if Fig. The ring is slightly disturbed so the it oscillates in its own plane. The time period of oscillation of the ring is
View Solution

