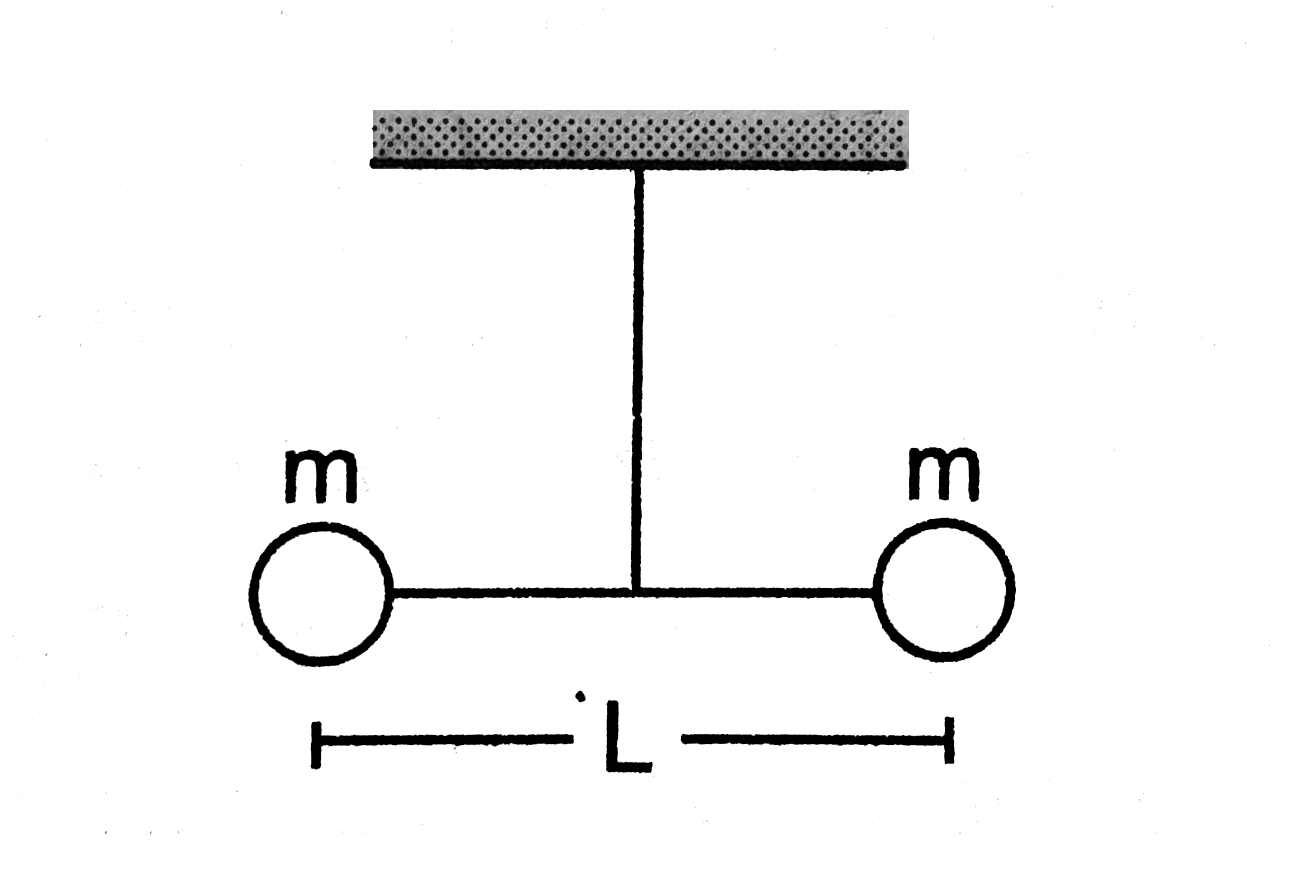
Two small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle θ0 and released. Find the tension in the rod as the system passes through the mean position.
√k2θ40+4m2g2L22L
√k2θ40+m2g6(2)L2L
kθ202L
kθ20+mgLL
The correct Answer is:B
at mean position, tension is
T=√(mg)2+(mω2L2)2→(1)
from law of conservation of enegry 12Iω2=12kθ20
⇒ω2=kθ20I=kθ202(mL24)=2kθ20mL2→(2)
from (1) & (2) T can be solved.
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-I
2 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage
33 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-V
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
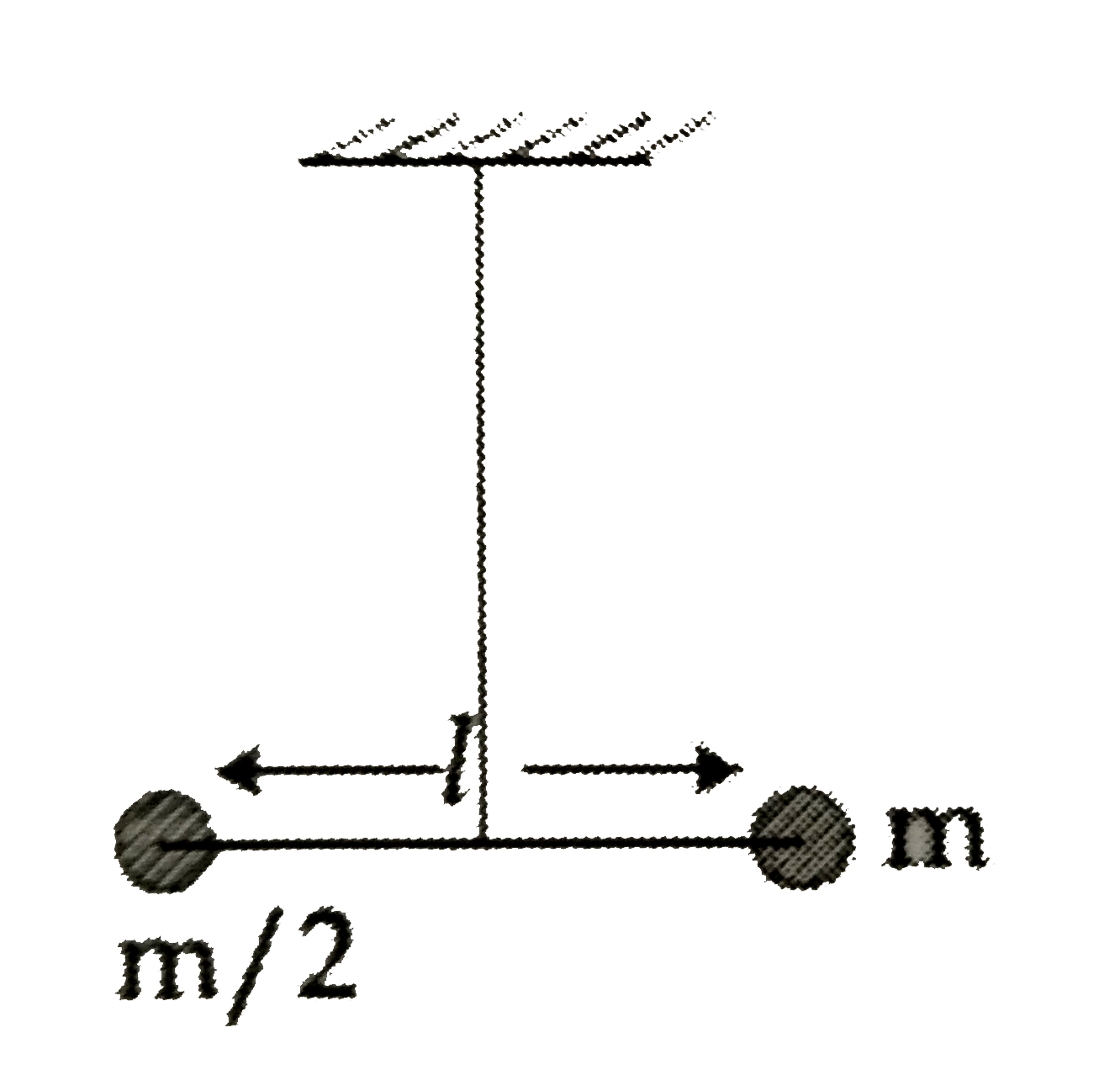
Two masses m and m2 are connected at the two ends of a massless rigid rod of length l. The rod is suspended by a thin wire of torsional constant k at the centre of mass of the rod-mass system(see figure). Because of torsional constant k, the restoring torque is τ=kθ for angular displacement θ. If the rod is rotated by θ0 and released, the tension in it when it passes through its mean position will be :
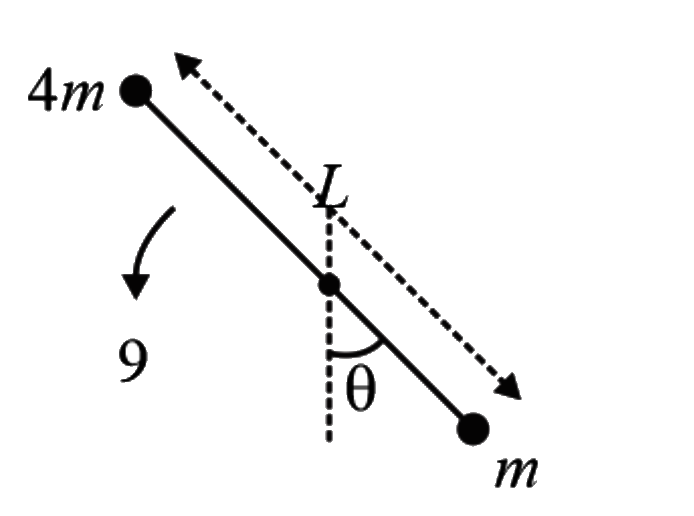
View SolutionTwo point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View Solution
Knowledge Check
Two small balls A and B of positive charge Q each and masses m and 2m respectively are connected by a non conducting light rod of length L. This system is released in a uniform electric field of strength E as shown. Just after the release (assume no other force acts on the system)
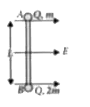 Arod has zero angular accelerationBrod has angular acceleration QE2mL in anti-clockwise direction.Cacceleration of point A is 2QE3m towards rightDacceleration of point A is QEm towards right.
Arod has zero angular accelerationBrod has angular acceleration QE2mL in anti-clockwise direction.Cacceleration of point A is 2QE3m towards rightDacceleration of point A is QEm towards right.Two small balls A and B of positive charge Q each and masses m and 2m, respectively, are connected by a non conducting light rod of length L. This system is released in a uniform electric field of strength E as shown. Just after the release (assume no other force acts on the system)
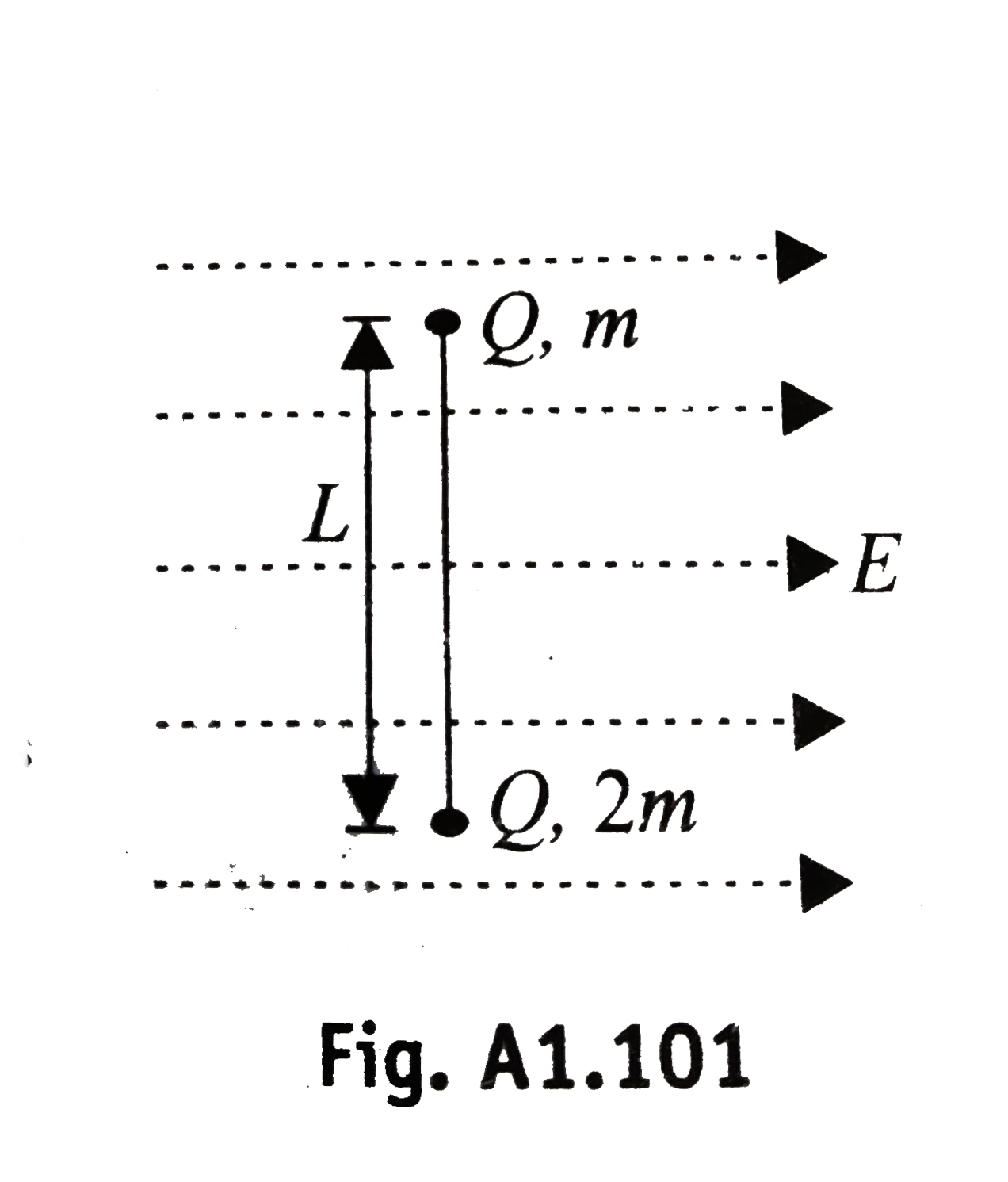 Arod has angular acceleration QE/2mL in anticlockwise direction.Brod has angular acceleration QE/2mL in anticlockwise directionCacceleration of point A is 2QE/3m toward rightDacceleration of point A is QE/m toward right .
Arod has angular acceleration QE/2mL in anticlockwise direction.Brod has angular acceleration QE/2mL in anticlockwise directionCacceleration of point A is 2QE/3m toward rightDacceleration of point A is QE/m toward right .Two particles, each of mass m and charge q are attached to the two ends of a light rigid rod of length 2R. The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
AqmB2qmCq2mDqπm
Two beads each of mass m are welded at the ends of two light rigid rods each of length l. if the pivots are smooth, find the ratio of translational and rotational kinetic energy of system.
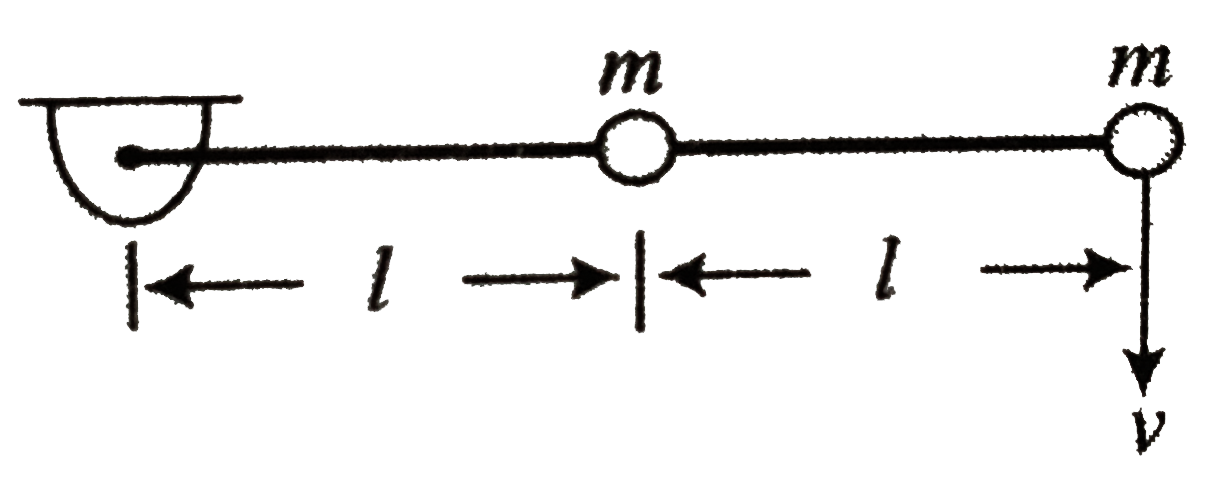
View SolutionTwo balls of mass m and 4m are connected by a rod of length L. The mass of the rod is small and can be treated as zero . The size of the balls also can of the neglected . We also assume the centre of the rod is hinged ,but the rod can rotate about its centre in the vertical plane without friction . What is the gravity - induced angular acceleration of the rod when the angle between the rod and the vertical is θ as shown ?
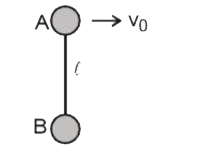
View SolutionTwo small spheres A & B respectively of mass m & 2m are connected by a rigid rod of length l & negligible mass. The two spheres are resting on a horizontal, frictionless surface. When A is suddenly given the velocity v0 as shown. Find velocities of A & B after the rod has rotated through 180∘ .
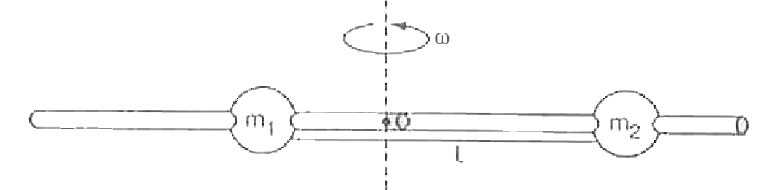
View SolutionTwo balls of masses m1=0.5kgandm2=0.3kg are connected by a nonstretchable string and slipped on to a horizontal , light rod. The rod is rotated with ω=110 rpm about a vertical axis passing through its centre. Find the tension of the string and the distance of the masses from the axis of rotation if l=20 cm is the length of the string. Is the equilibrium of the balls stable ?
View SolutionTwo masses each of mass M are attached to the end of a rigid massless rod of length L. The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
View Solution
