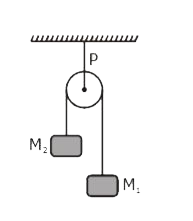
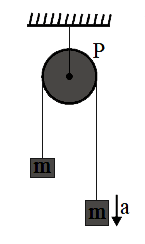
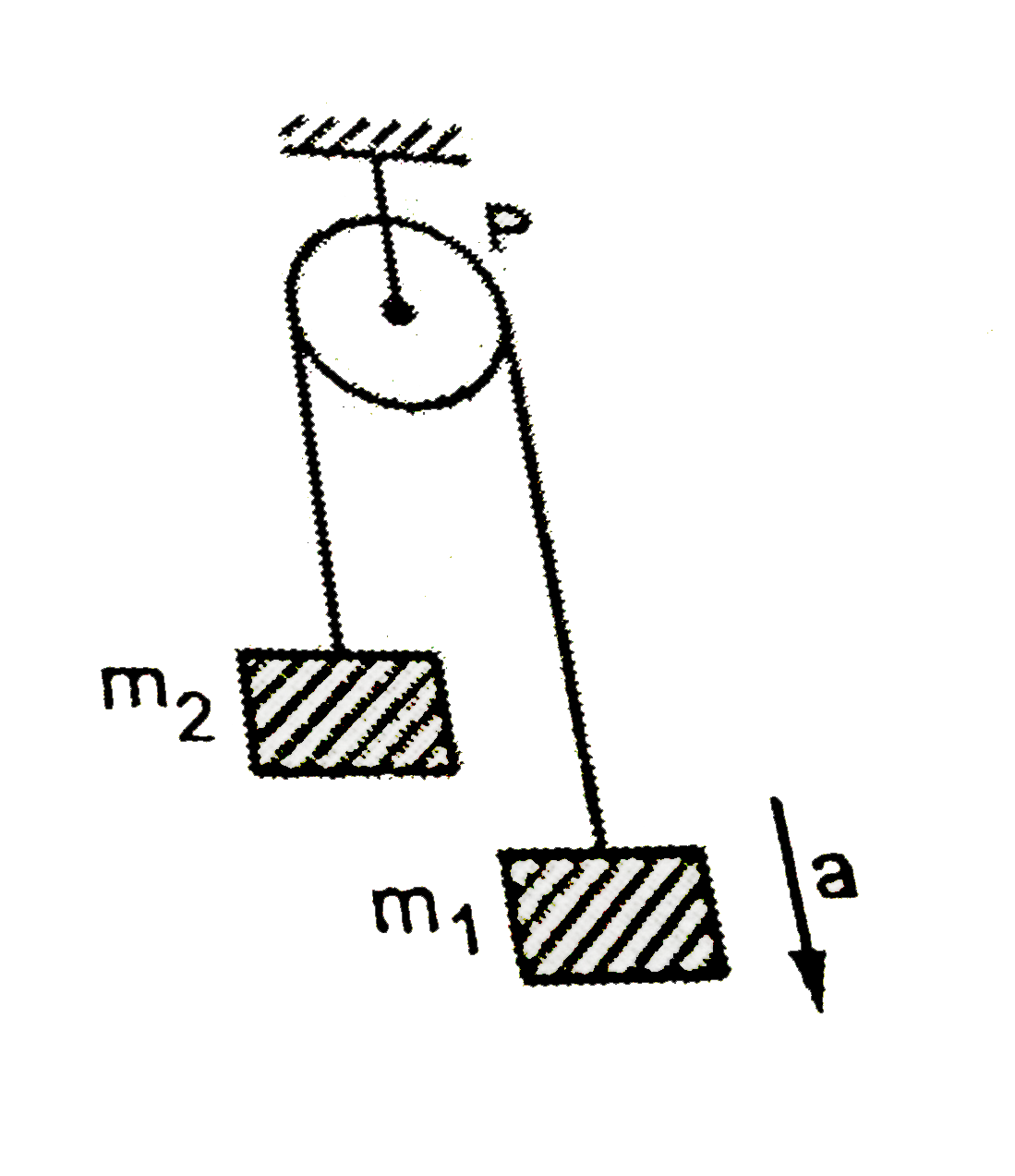
In the figure, the blocks unequal masses m1 and m2 (m1<m2).m2 has a downward acceleration a. The pulley P has a radius r, and some mass. The string does not slip on the pulley. Find the acceleration of block and angular acceleration of pulley. (I = momentum of inerita of pulley)
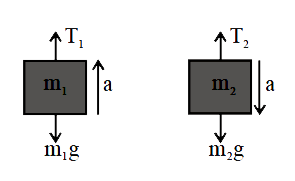
T1−m1g=m1a…(1)
m2g−T2=m2g …(2)
Total toreque = Iα
(T2−T1)P=Iα...(3)
a=α ...(4)
By. Eq (1), (2) (3) and (4) ⇒
a=(m2−m1)m2+m1+Ir2g⇒α=ar
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 1
90 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
Knowledge Check
In the figure, the blocks have unequal masses m1 and m2(m1>m2).m1 has a downward acceleration a . The pulley P has a radius r, and some mass. The string does not slip on the pulley.AThe two sections of the string have unequal tensions.BThe two blocks have acceleration of equal magnitude.CThe angular acceleration of P is a/r.Da<(m1−m2m1+m2)A block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
Amg2m+MB2mgm+MCmgm+MD2mg2m+MIf the string & all the pulleys are ideal, acceleration of mass m is :-
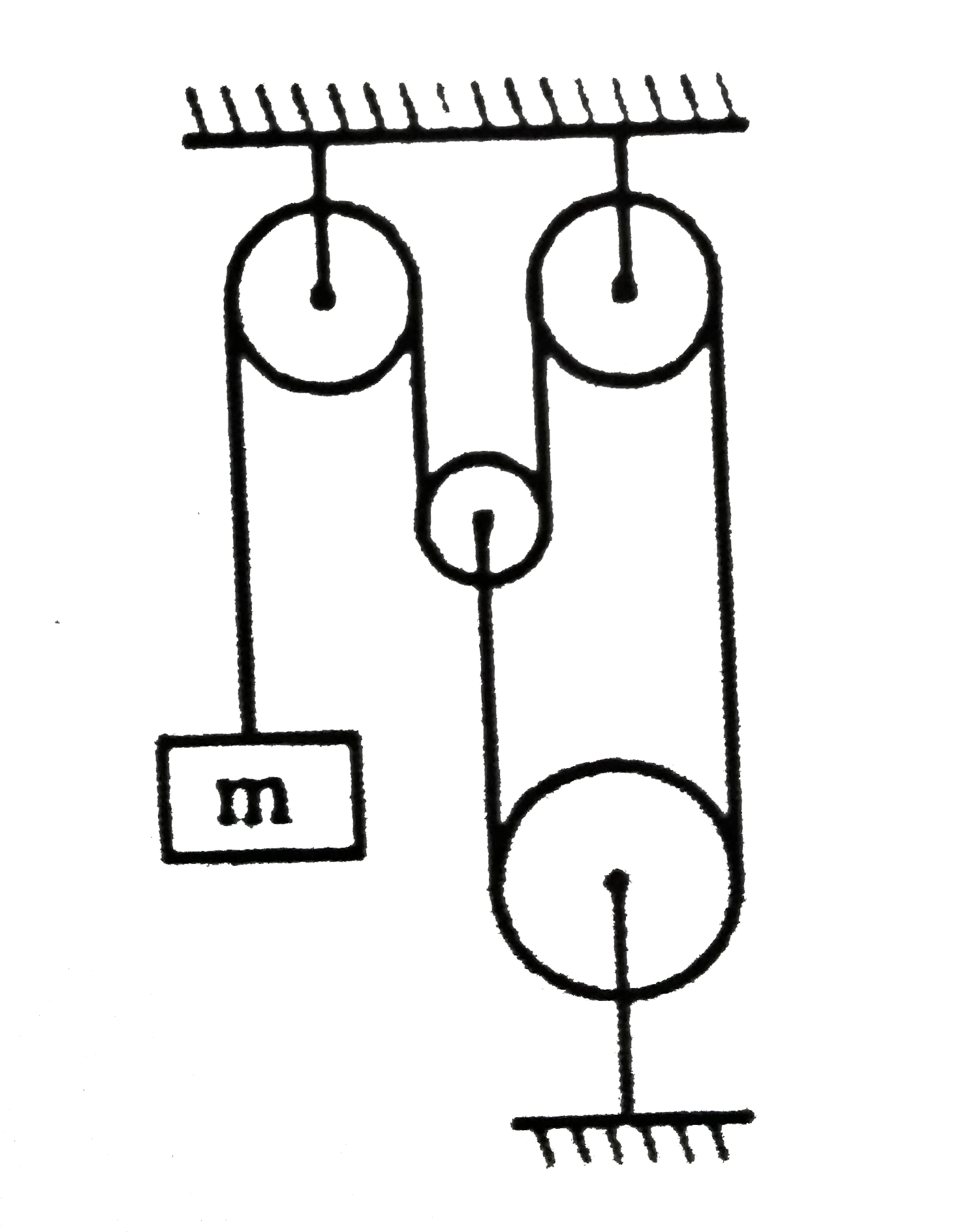 Ag2B0CgDdependent on m
Ag2B0CgDdependent on m
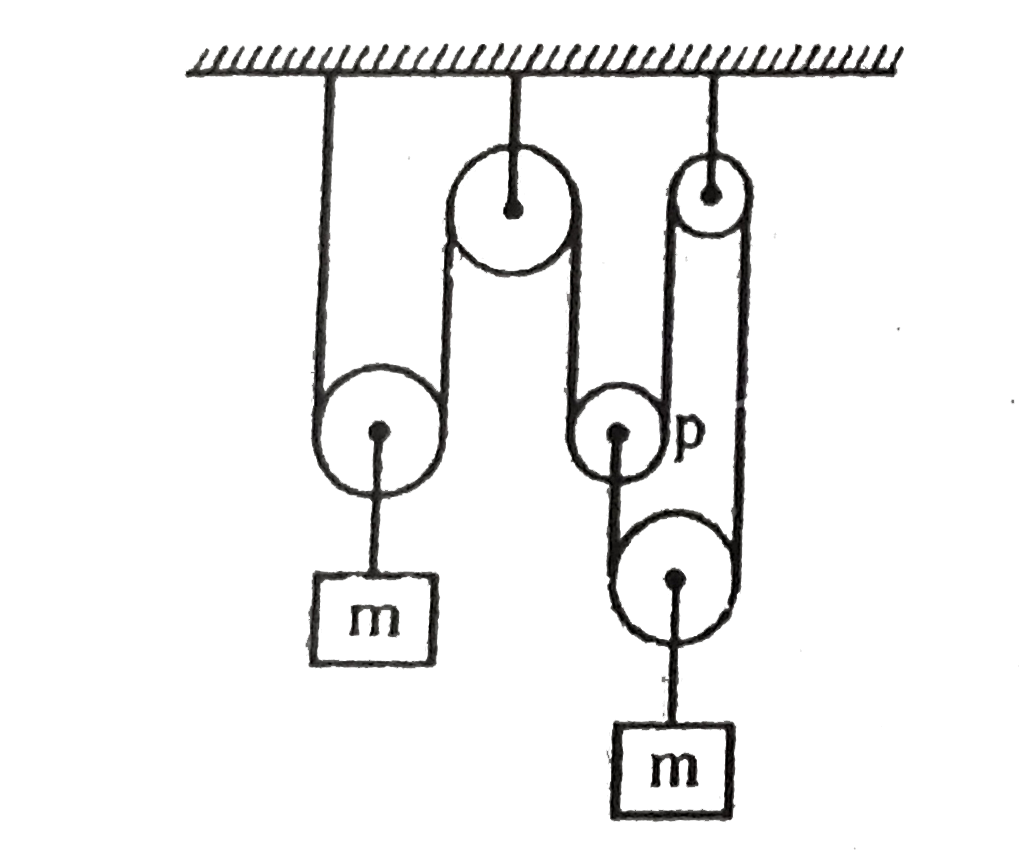
All pulleys are massless The string is light and inextensible Find acceleration of centre of pulley 'p'∈m/s2
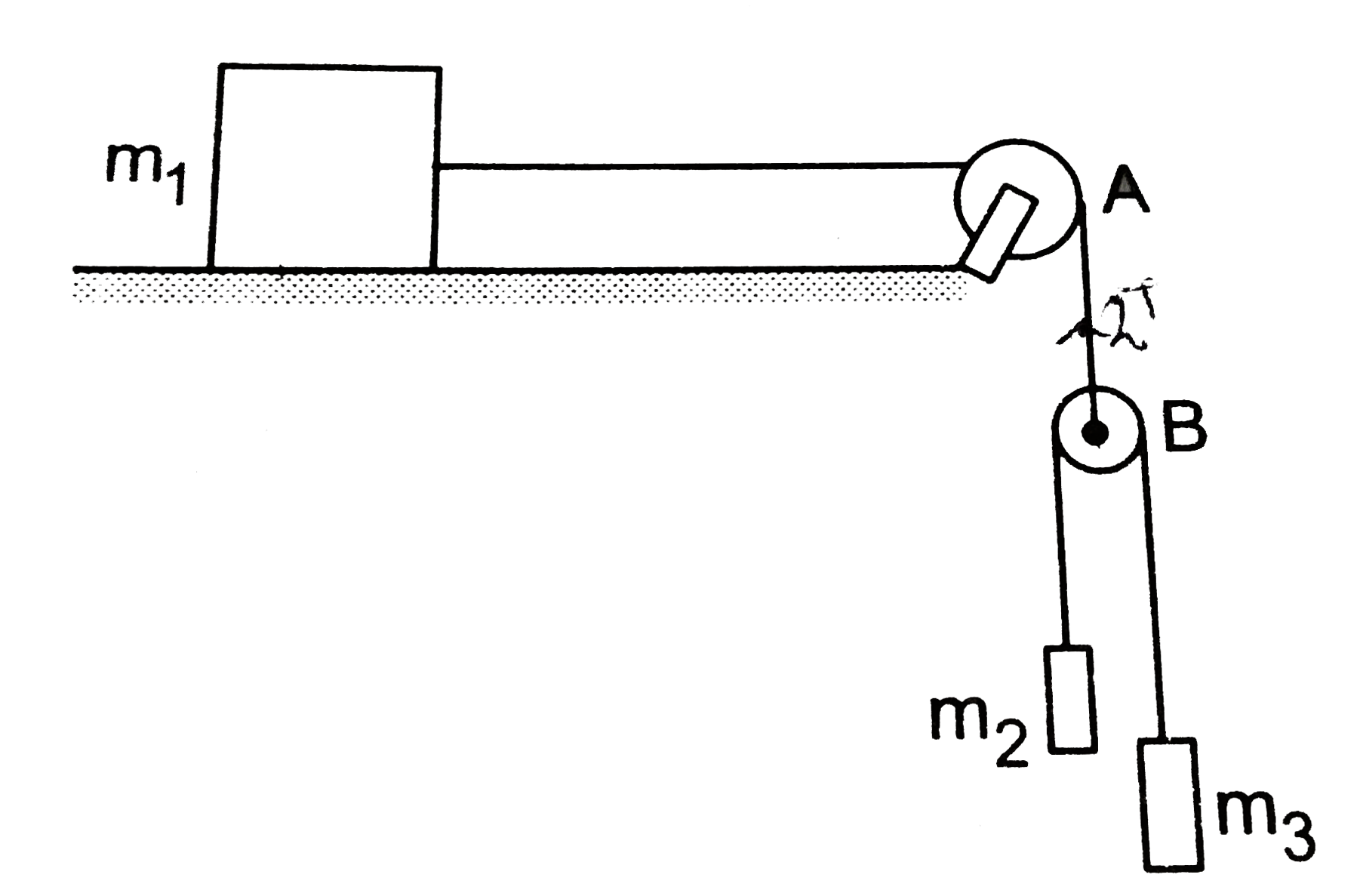
View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
View SolutionAn object of mass m is tied to a light string wound around a pulley that has a moment of inertia I and radius R. The wheel bearing is fricrtionless and the string does not slip on the run. Find the tension in the string and the acceleration of the object.
View SolutionFor the given figure the acceleration of 1 kg block if string is massless and mass of pulley is 2 kg and diameter of pulley is 0.2 m :-
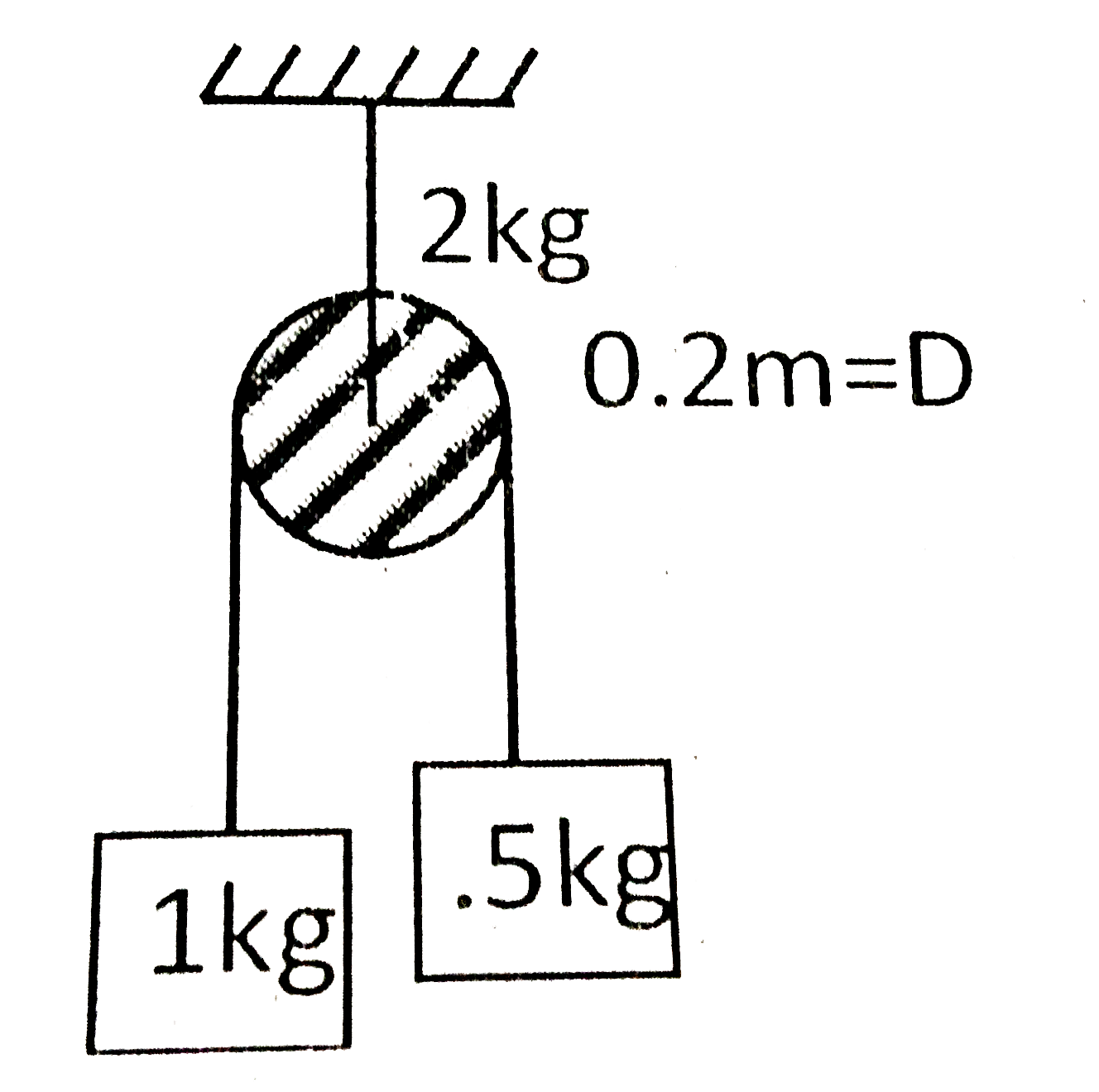
View SolutionFind the acceleration of the block of mass m. Assume pulleys are massless and frictionless.

View Solution