A small bar A resting on a smooth horizontal plane is attached by threads to a point P(figure) and, by means of a weightless pulley, to a weight B possessing the same mass as the bar itself.
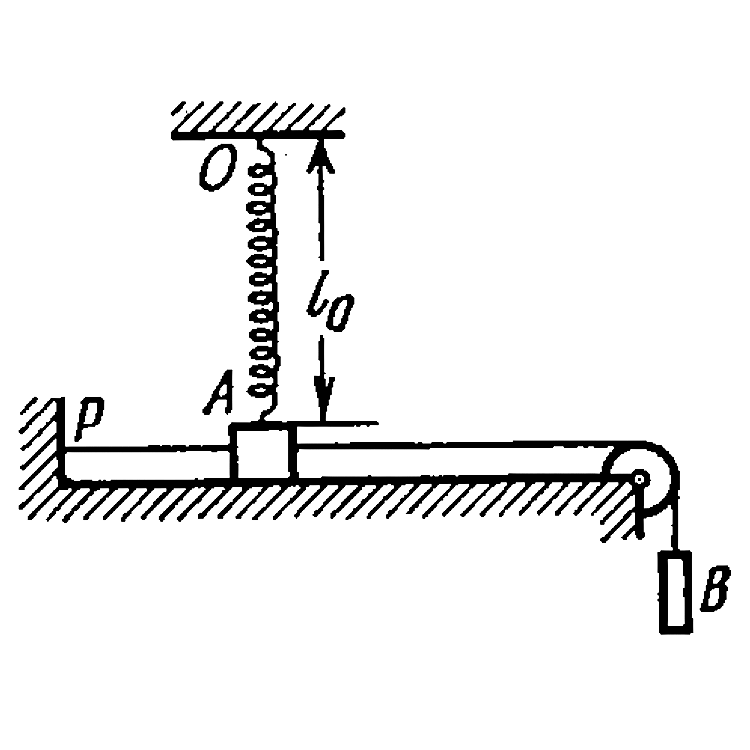
Besides, the bar is also attached to a point O by means of a light non-deformed spring of length l0=50cm and stiffness x=5mg/l0, where m is the mass of the bar. The thread PA having been burned, the bar starts moving. Find its velocity at the moment when it is breaking off the plane.
When the thread PA is burnt, obviously the speed of the bars will be equal at any instant of time until it breaks off. Let v be the speed of each block and θ be the angle, which the elongated spring makes with the vertical at the moment, when the bar A breaks off the plane. At this stage the elongation in the spring.
Δl=l0secθ−l0=l0(secθ−1) (1)
Since the problem is concerned with position and there are no forces other than conservative forces, the mechanical energy of the system (both bars + spring) in the field of gravity is conserved, i.e. ΔT+ΔU=0
So, 2(12mv2)+12kl20(secθ−1)2−mgl0tanθ=0 (2)
From Newton's second law in projection form along vertical direction:
mg=N+kl0(secθ−1)cosθ
But, at the moment of break off, N=0.
Hence, kl0(secθ−1)cosθ=mg
or, cosθ=kl0−mgkl0 (3)
Taking k=5mgl0, simultaneous solution of (2) and (3) yields:
v=√19gl032=1⋅7m/s.

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Universal Gravitation
34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Dynamics Of A Solid Body
56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - The Fundamental Equation Of Dynamics
59 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
A planet of mass M moves along a circle around the Sun with velocity v=34.9km/s (relative to the heliocentric reference frame). Find the period of revolution of this planet around the Sun.
View SolutionA thin uniform rod AB of mass m=1.0kg moves translationally with acceleration w=2.0m/s2 due to two antiparallel forces F1 and F2 (figure). The distance between the points at which these forces are applied is equal to a=20cm. Besides, it is known that F2=5.0N. Find the length of the rod.
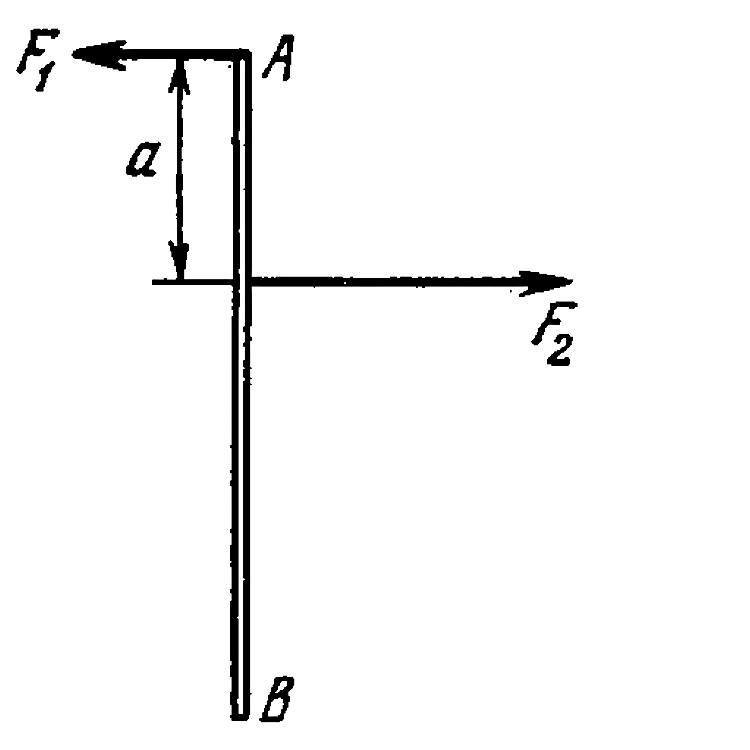
View SolutionAn aerostat of mass m starts coming down with a constant acceleration w. Determine the ballast mass to be dumped for the aerostat to reach the upward acceleration of the same magnitude. The air drag is to be neglected.
View SolutionAn electromagnetic wave of frequency v=3.0MHz passes from vacuum into a dielectric medium with permittivity ε=4.0. Then
View SolutionCalculate what fraction of gas molecules
(a) traverses without collisions the distances exceeding the mean free path λ ,
(b) has the free path values lying within the inerval from λ to 2λ.
View SolutionTwo bars of masses m_1 and m_2 connected by a weightless spring of stiffness k , rest on a smooth horizontal plane. Bar 2 is shifted by a small distance x_0 to the left and released. The veloicyt of the centre of mass of the system when bar 1 breaks off the wall is
View SolutionA horizontal plane supports a plank with a bar of mass m placed on it and attached by a light elastic non-deformed cord of length l_0 , to a point O. The coefficient of friciton between the bar and the plank is equal to m . The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord derivates from the vertical by an angle theta . Find the work that has been performed by the moment by the frictional force acting on the bar in the reference frame fixed to the plane.
View SolutionA small bar A resting on a smooth horizontal plane is attached by threads to a point P and by means of weightless pulley, to a weight B possessing the same mass as the bar itself. The bar is also attached to a point O by means of a light non-deformed spring of length l0=50cm and stiffness k=mg/l0, where m is the mass of the bar. The thread PA having been burned, the bar starts moving to the right. Find its velocity at the moment when it is breaking off the plane.

View SolutionTwo bars of masses m1 and m2 connected by a non-deformed light spring rest on a horizontal plane. The coefficient of friction between the bars and the surface is equal to k. What minimum constant force has to be applied in the horizontal direction to the bar of mass m1 in order to shift the other bar?
View SolutionA horizontal plane supports a plank with a bar of mass m=1.0kg placed on it and attached by a light elastic non-deformed cord of length l0=40cm to a point O(figure). The coefficient of friction between the bar and the plank equals k=0.20. The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord deviates from the vertical by an angle θ=30∘. Find the work that has been performed by that moment by the friction force acting on the bar in the reference frame fixed to the plane.

View SolutionA smooth light horizontal rod AB can rotate about a vertical axis passing through its end A. The rod is fitted with a small slieeve of mass m attached to the end A by a weightless spring of length l_0 and stiffness x . What work must be performed to slowly get this system going and reaching the angular velocity omega ?
View SolutionTwo bars of masses m1 and m2 connected by a weightless spring of stiffness ϰ (figure) rest on a smooth horizontal plane.

Bar 2 is shifted a small distance x to the left and then released. Find the velocity of the centre of inertia of the system after bar 1 breaks off the wall.
View SolutionTwo bars connected by a weightless spring of stiffness ϰ and length (in the non-deformed state) l_0 rest on a horizontal plane. A constant horizontal force F starts acting on one of the bars as shown in figure. Find the maximum and minimum distances between the bars during the subsequent motion of the system, if the masses of the bars are: (a) equal: (b) equal to m_1 and m_2 , and the force F is applied to the bar of mass m_2 .
View SolutionA bar of mass m=0.50kg lying on a horizontal plane with a friction coefficient k=0.10 is attached to the wall by means of a horizontal non - deformed spring. The stiffness of the spring is equal to x=2.45 N//cm , its mass is negligibl . The bar was displaced so that the spring was stretched by x_(0)=3.0 cm , and then released. Find : (a) the period of oscillation of the bar , (b) the total number os osciallations that the bar performs untial it stops completely.
View SolutionTwo bars of masses m_(1) and m_(2) connected by a non - deformed light spring rest on a horizontal plane. The coefficient of friction between the bars and the surface is equal to mu . What minimum constant force has to be appled in the horizontal direction to the bar of mass m_(1) in order to shift the other bar?
View Solution
