A horizontal plane supports a plank with a bar of mass m placed on it and attached by a light elastic non-deformed cord of length l0, to a point O. The coefficient of friciton between the bar and the plank is equal to m. The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord derivates from the vertical by an angle θ.
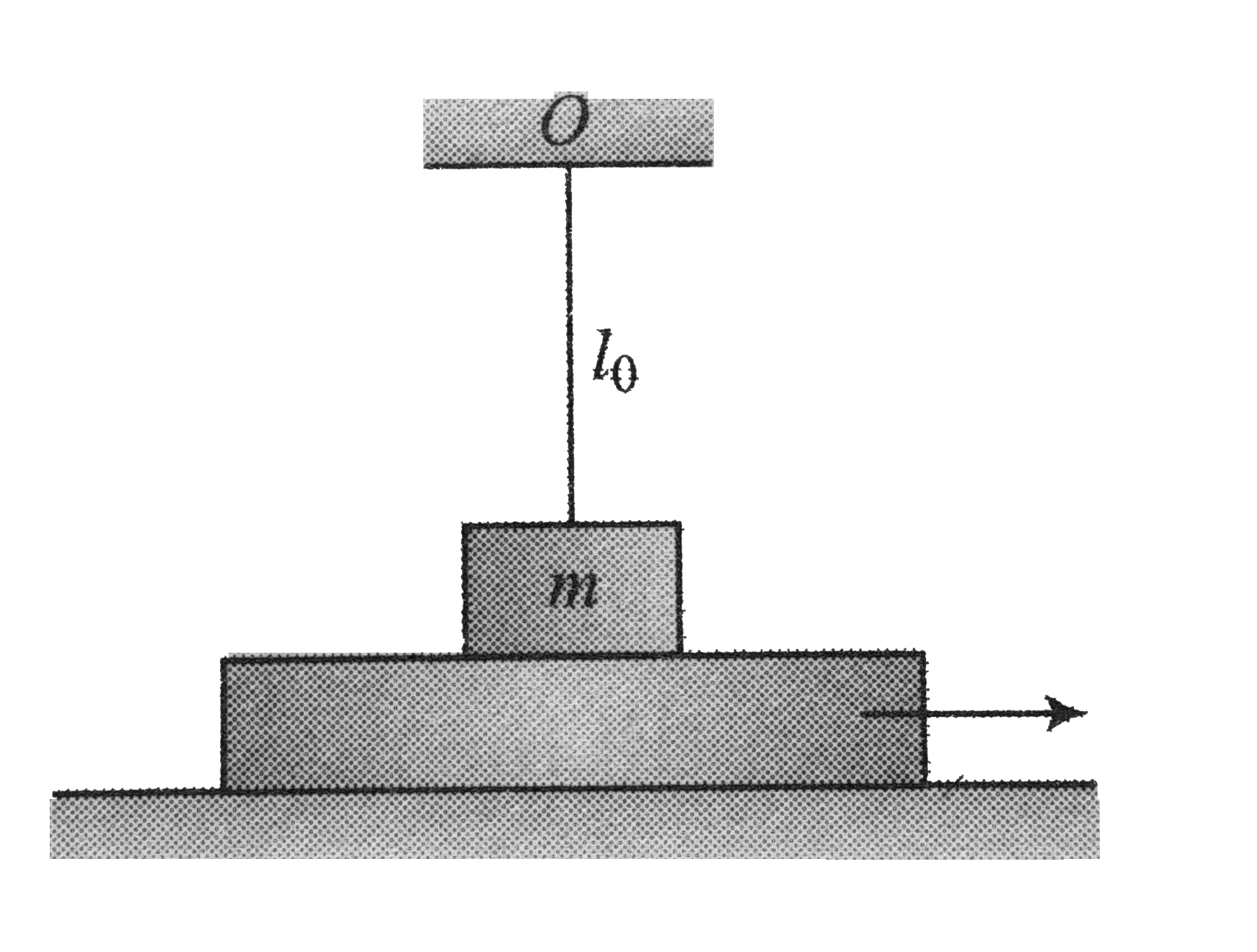
Find the work that has been performed by the moment by the frictional force acting on the bar in the reference frame fixed to the plane.
When the plank is pulled to the right, bar also moves to the right with the plank, and elastic cord elongates. Hence, a tension is developed in it.
Since the bar starts sliding over the plank when inclination of the elastic cord becomes equal to θ with the vertical, therefore at this moment, friction acting between the bar and the plank is at its limiting value.
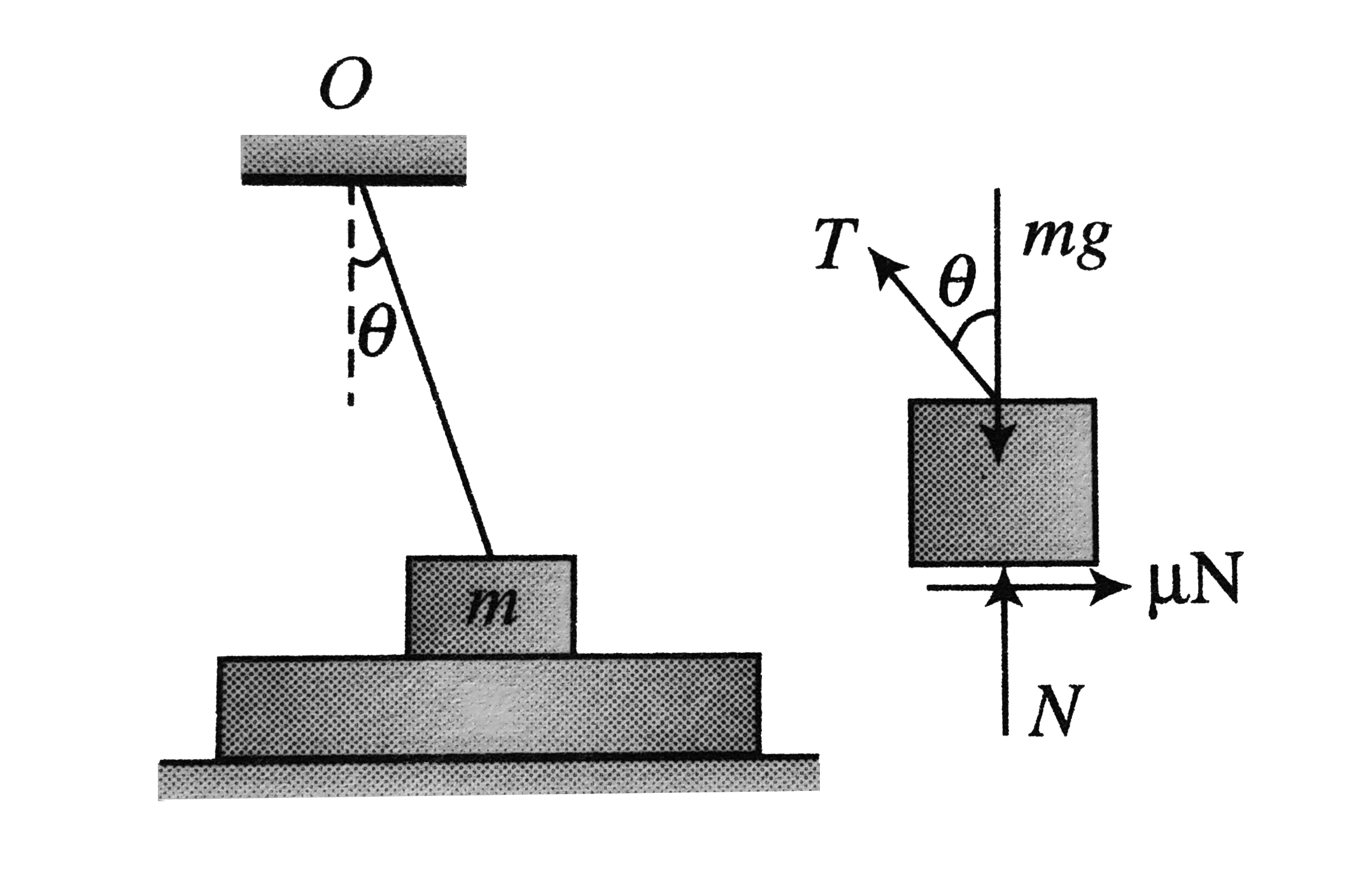
Let the force constant of the elastic cord be K. Then tension in it will be equal to T=KΔl, where Δl is elongation of the cord. It is equal to Δl=(l0secθ−l0)
T=K⋅l0(secθ−1)
Now considering FBD of the bar, for vertical equilibrium,
N+Tcosθ=mg
N=(mg−Tcosθ)
For horizontal equilibrium, μN=Tsinθ
μ(mg−Tcosθ)=Tsinθ
Substituing, T=K.l0(secθ−1)
K=μmgl0(secθ−1)(sinθ+μcosθ)
Since there is not slipping between the bar and plank up to this moment, therefore no energy is lost against friction.
Since the only force responsible for rightward displacement of the bar and hence for elongation of the cord is friction, therefore whole of the work done by the friction is used to elongate the cord. In fact it is stored in the cord in the form of its deformation energy.
Hence, the work that has been performed by the moment by the frictional force acting on the bar in the reference frame fixed to the plane is equal to 12K(Δl)2.
⇒W=12μmgl0(secθ−1)(sinθ+μcosθ)
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.1
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.2
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Archives (integer)
Explore 4 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A horizontal plane supports a plank with a bar of mass m=1.0kg placed on it and attached by a light elastic non-deformed cord of length l0=40cm to a point O(figure). The coefficient of friction between the bar and the plank equals k=0.20. The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord deviates from the vertical by an angle θ=30∘. Find the work that has been performed by that moment by the friction force acting on the bar in the reference frame fixed to the plane.

View SolutionTwo bars of masses m1 and m2 connected by a non-deformed light spring rest on a horizontal plane. The coefficient of friction between the bars and the surface is equal to k. What minimum constant force has to be applied in the horizontal direction to the bar of mass m1 in order to shift the other bar?
View Solution
Knowledge Check
A horizontal plane supports a plank with a block placed on it. A light elastic string is attached to the block, which is attached to a fixed point O. Initially, the cord is unstretched and vertical. The plank is slowly shifted to right until the block starts sliding over it. It occurs at the moment when the cord deviates from vertical by an angle θ=0∘. Work done by the force F equals
 A(a) Energy lost against friction F1 plus strain energy in cordB(b) Work done against total friction acting on the plank aloneC(c) Work done against total friction acting on the plank plus strain energy in the cordD(d) Work done against total friction acting on the plank plus strain energy in the cord minus work done by friction acting on the block
A(a) Energy lost against friction F1 plus strain energy in cordB(b) Work done against total friction acting on the plank aloneC(c) Work done against total friction acting on the plank plus strain energy in the cordD(d) Work done against total friction acting on the plank plus strain energy in the cord minus work done by friction acting on the blockTwo bars of masses m1 and m2 connected by a non−deformed light spring rest on a horizontal plane. The coefficient of friction between the bars and the surface is equal to μ. What minimum constant force has to be appled in the horizontal direction to the bar of mass m1 in order to shift the other bar?
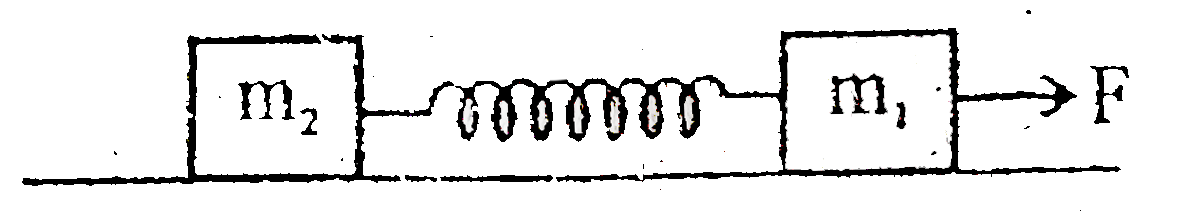 A(m1+m22)μgB(m2+m12)μgC(m1−m22)μgD(2m2+m12)μg
A(m1+m22)μgB(m2+m12)μgC(m1−m22)μgD(2m2+m12)μgA plank of mass 3m is placed on a rough inclined plane and a man of mass m, the coefficient of friction between the board and inclined plane is μ=0.5, the minimum acceleration of man so that plank does not slide is :
 A8m/s2B4m/s2C6m/s2D3m/s2
A8m/s2B4m/s2C6m/s2D3m/s2
A plank with a bar placed on it performs horizontal harmonic oscillations with amplitude a=10cm. Find the coefficient of friction between the bar and the plank if the former starts sliding along the plank when the amplitude of oscillation of the plank becomes less than T=1.0s.
View SolutionA bar of mass m1 is placed on a plank of mass m2 which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t0 at which the plank starts sliding is :

View SolutionA plank of mass 3m is placed on a rough inclined plane and a man of mass m walks down the board. If the coefficient of friction between the board and inclined plane is μ=0.5, the minimum acceleration of does not slide is:

View SolutionA block is placed over a plank. The coefficient of friction between the block and the plank is μ=0.2. Initially both are at rest, suddenly the plank starts moving with acceleration a0=4m/s2. The displacement of the block in 1 is (g=10m/s2)
View SolutionA long plank of mass M is initially at rest on a frictionless surface. A small block with mass m and initial speed u0 slides on top of the larger plank. The coefficient of friction between the block and plank is μ
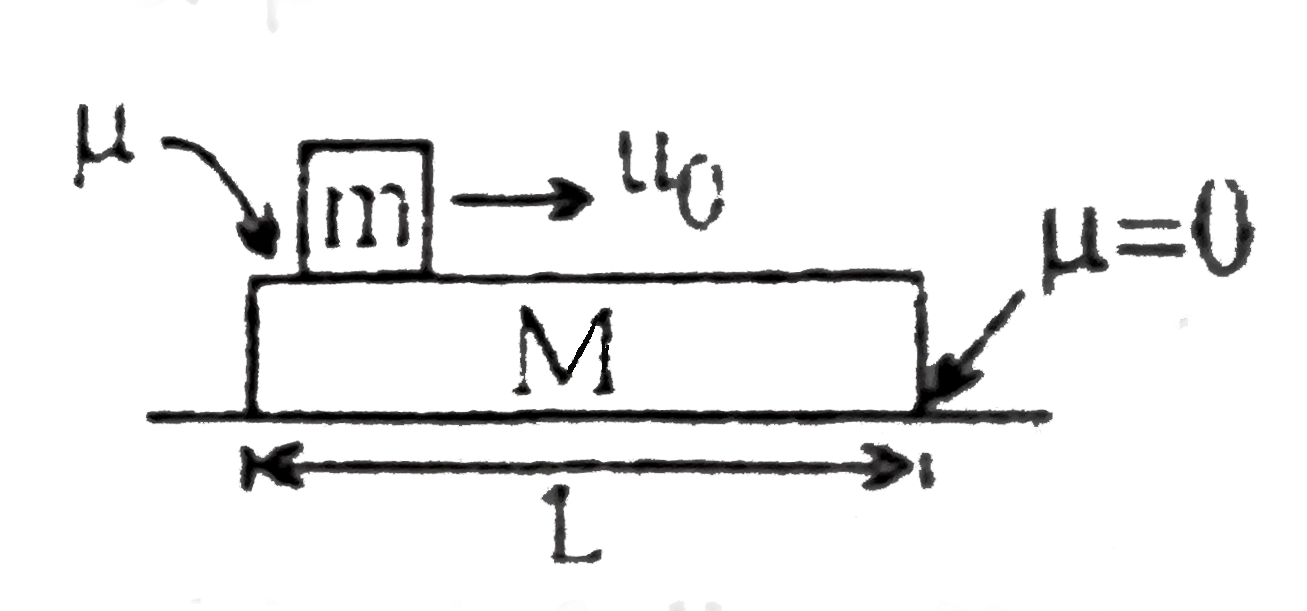
Net work done by friction if the top block falls off the plank after sliding over its length L is
View Solution

