Block of mass m are released from rest and they slide down the inclined surface as shown in figure. Show that the work done by the frictional forces on the blocks are same in all the cases. Also calculate the speeds with which the blocks reach point B. The coefficient of friction for all the surface is μk.

For figure (a)
Frictional force on the block =μkN=μkmgcosθ
If S be the length of the incline, work done by the frictional force on the block when the block slides down from A to B,
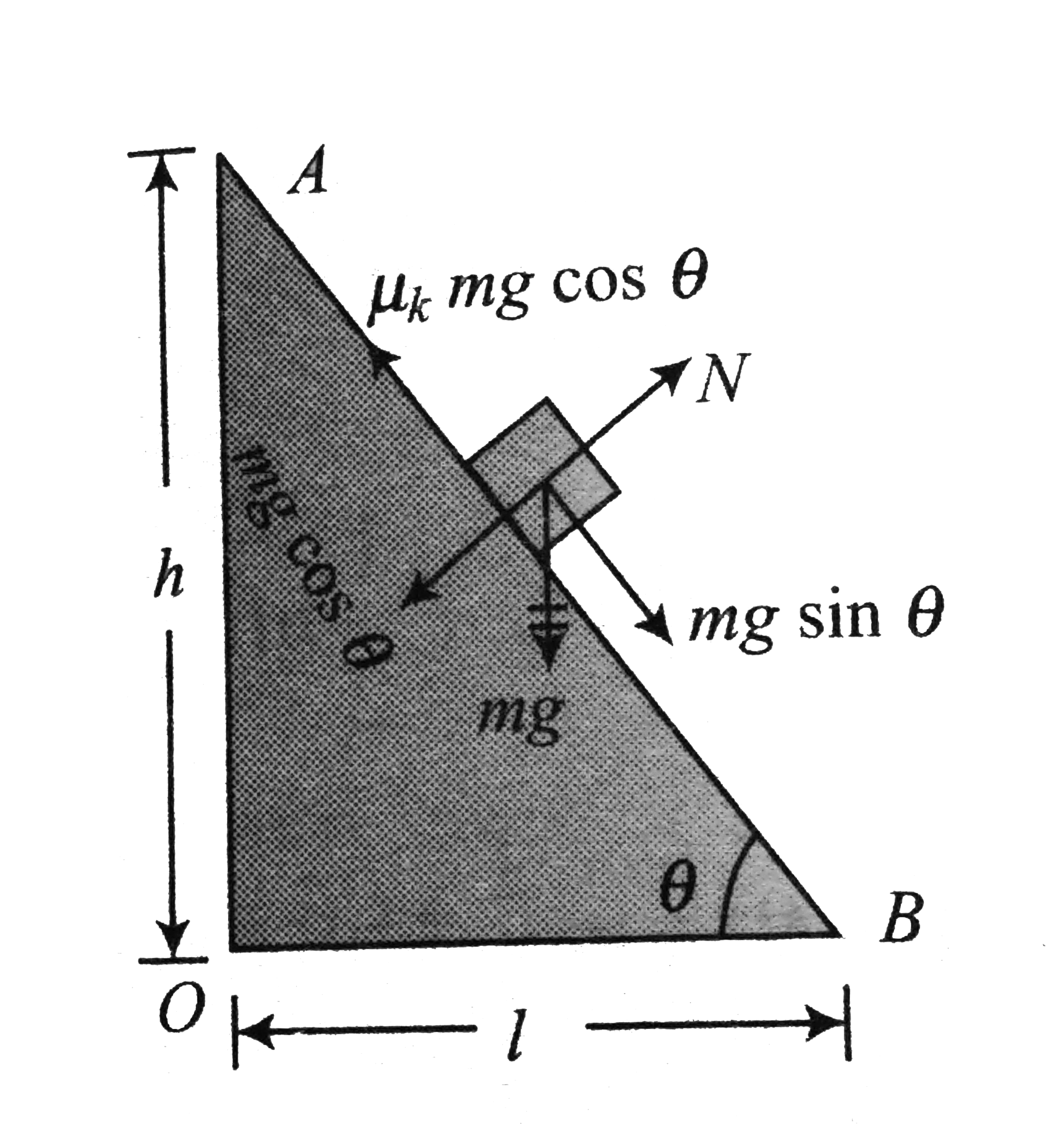
Wfl=(μkmgcosθ)(s)
{Force and displacement are antiparallel}
=−μkmg(scosθ)=−μkmg
Figure (b)
Frictional forces on the block at the plans with the inclination θ1 and θ2 are μkmgcosθ1 and μkcosθ2. If the lengths of the planes be S1 and S2, work done by fricitional force on the block,

Wfk=−(μkmgcosθ1)s1−(μkmgcosθ2)s2
=−μkmg(s1cosθ1+s2cosθ2)=−μkmgl
For Figure (c)
Let the length of the inclines with inclination θ1, θ2, and θ3 be s1, s2, and s3, respectilvey. At these planes, the frictional force on the block are μkmgcosθ1, μkmgcosθ2, and μkmgcosθ3, respectively. Work done by the frictional force on the block,
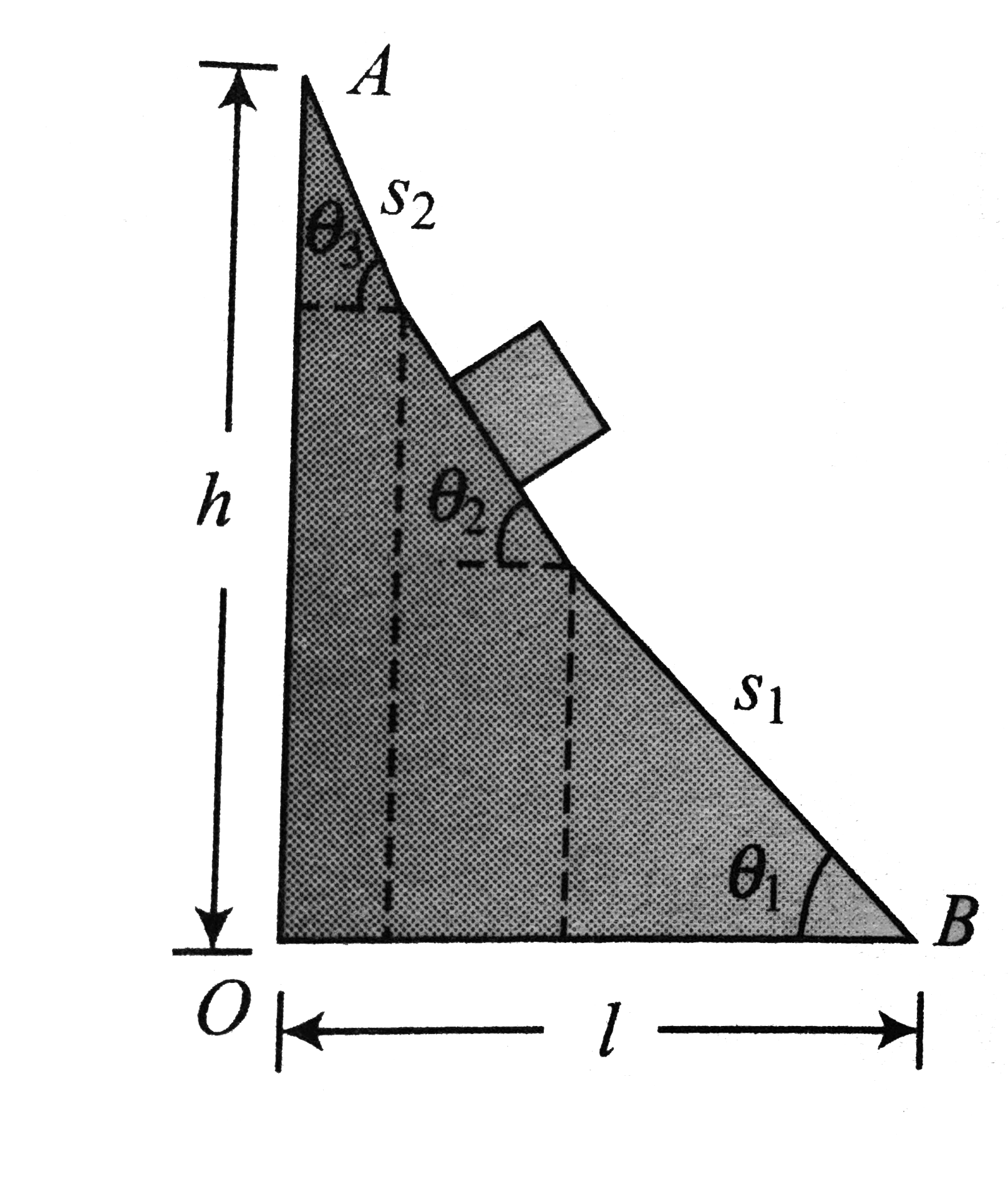
Wfk=−(μkmgcosθ1)s1−(μkmgcosθ2)s2−(μkmgcosθ3)s
=−μkmg(s1cosθ1+s2cosθ2+s3θ3)=−μkmgl.
For Figure (d)
Let the block be at point C where the tangent to the parabola makes an angle θ with the horizontal as shown in figure.
Frictional force on the block at
C=μkmgcosθ, as shown. Consider an infinitesimal displacement ds at C.
Work done by the frictional force over ds,

dW=μ1mgcosθds
Work done from A to B,
Wfk=∫BAdW∫BA−μkmgcosθds
=−∫BAμkmgdx=−μkmgl
Calculations show that the work done by the frictional force in each case are same.
Speed at B:
Using work-energy theorem.
Wmg=Wfk=K2−K1
⇒mgh−mkmgl=12mv2=0
(Block is at rest at A, K1=0)
⇒2g(h−mkl)=v2⇒v=√2g(h−μkl) 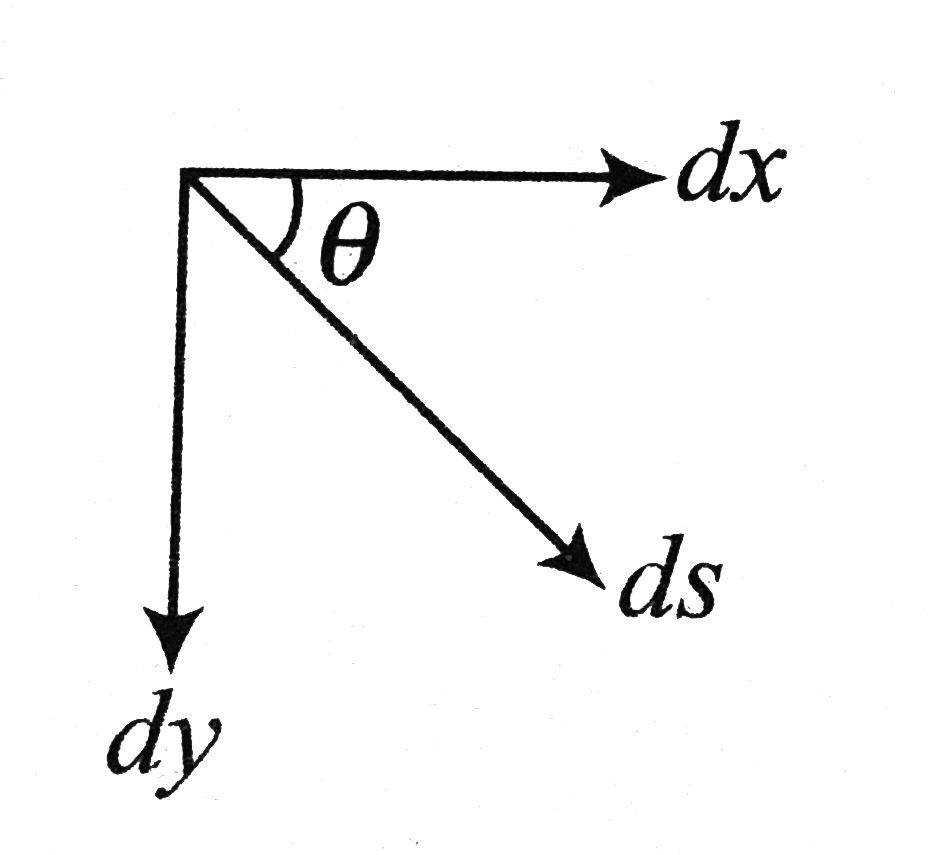
In each case, the block will reach B with same speed, which equals √2g(h−μkl).
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.1
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Exercise 8.2
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICSChapter:WORK, POWER & ENERGYExercise:Archives (integer)
Explore 4 Videos
- VECTORSBook:CENGAGE PHYSICSChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A block of mass m slides down on inclined wedge of same mass m as shown in figure . Friction is absent everywhere . Acceleration of centre of mass of the block and wedge is
View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

View Solution
Knowledge Check
A block of mass 10 kg is released from top of rough inclined plane as shown in the figure if coefficient of friction between the block and inclined plane is then total work done on the block by all the forces acting on it till it reaches the bottom s = 10 ms
A200 jB300 jC100 jD-200 jBlock A of mass M in the system shown in the figure slides down the incline at a constant speed. The coefficient of friction between block A and the surface is 1 3 3 . The mass of block B is-
 Am/2Bm/3C2m/3Dm/√3
Am/2Bm/3C2m/3Dm/√3A block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
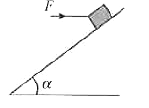 ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
A small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
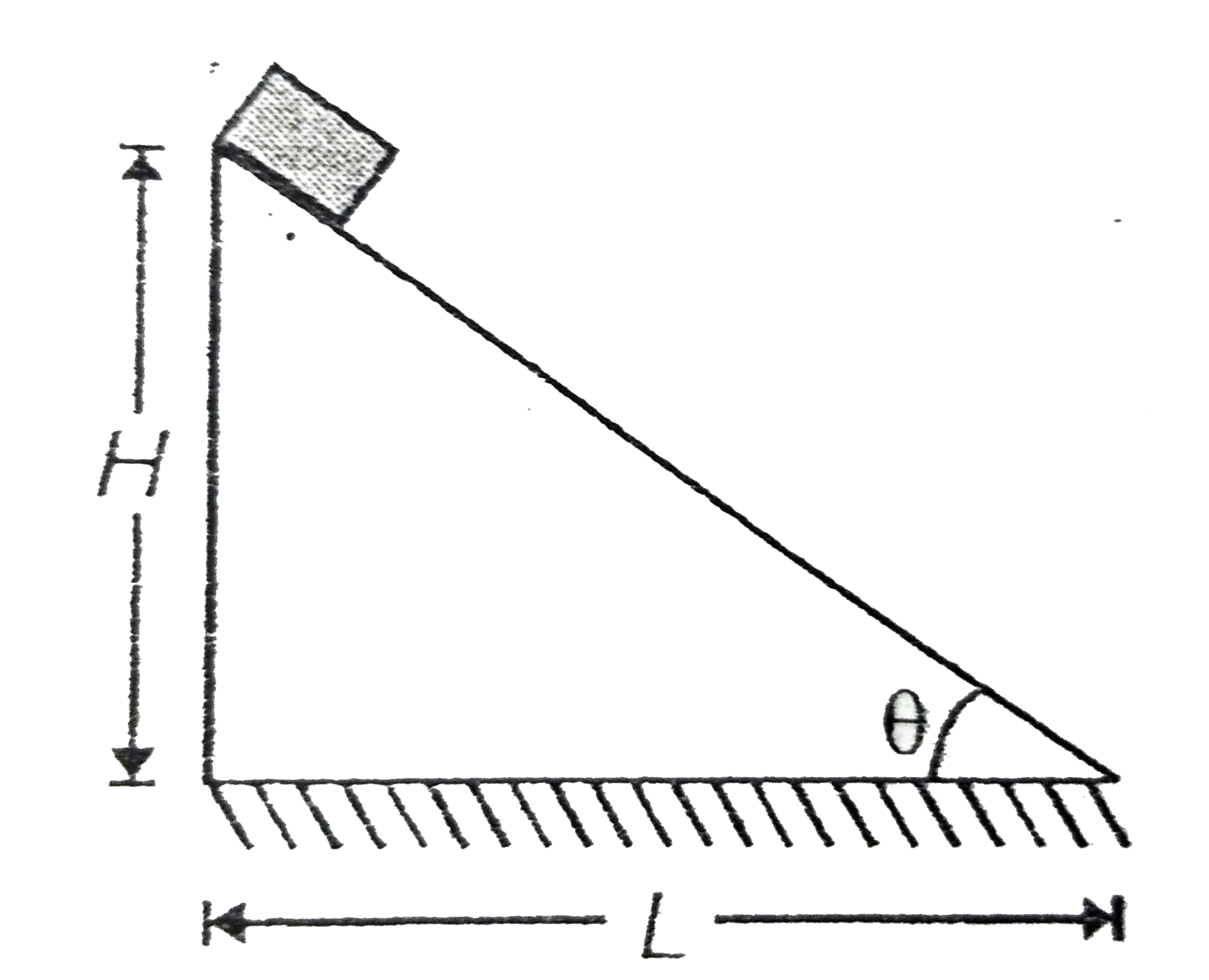
View SolutionA block of mass 4kg is released from the top of a rough inclines plane of height 10m. If velocity of the block is10ms at the bottom of the inclined then work done by the friction force on the block will be
View SolutionA block of mass m is released on the top of a smooth inclined plane of length x and inclination θ as shown in figure. Horizontal surface is rough. If block comes to rest after moving a distabce d on the horizontal surface, then coefficient of friction between block and surface is :-

View SolutionA block of mass 250 g slides down an incline of inclination 370 with a uniform speed. Find the work done against the friction as the block slides through 1.0 m.
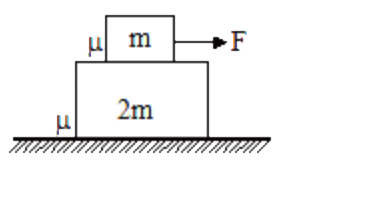
View SolutionThe system of two blocks is at rest an shown in the figure. A variable Horizontal force is applied to the upper block. The maximum possible constant force exerted by the horizontal ground surface on the lower block is ( coefficient of friction for both the contracts is μ )
View Solution

