A small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
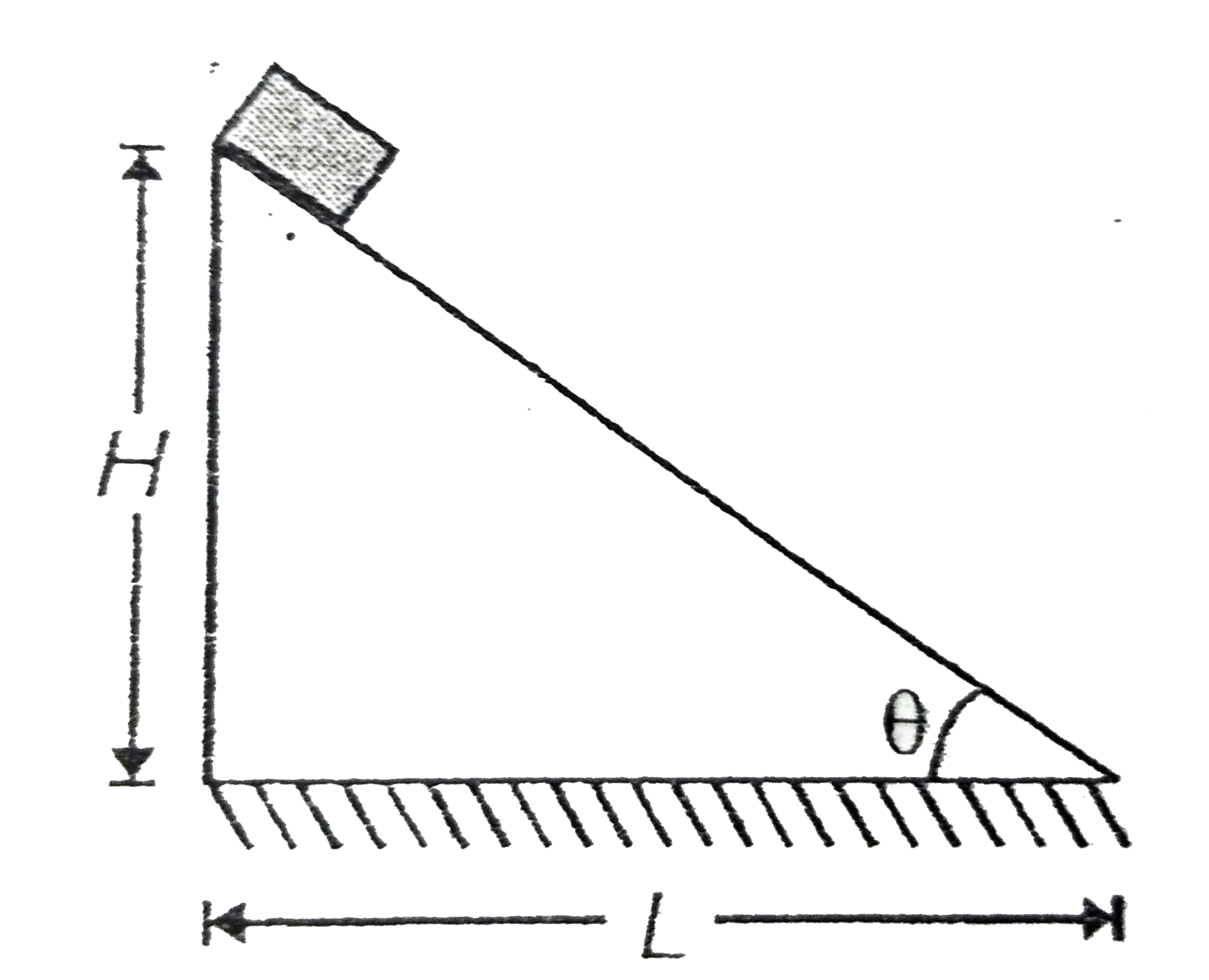
The FBD of the block is shown.
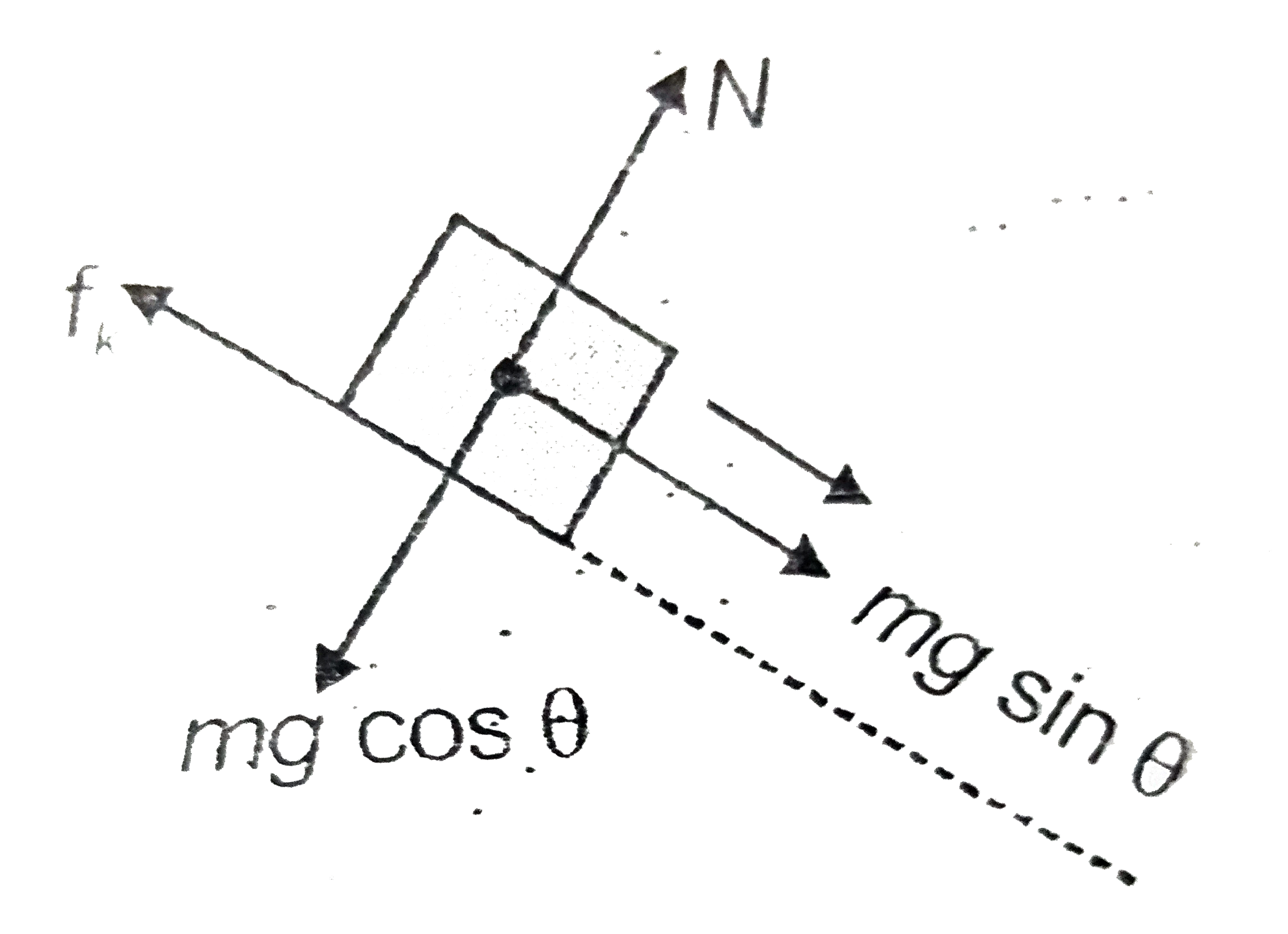
initial speed is zero final speed is v 12mv2=0=WTotal We shall find the work done by each force
(1) WN=0
(2) Wmgcosθ=0
(3) Wmgsinθ=mgsinθ×S×cos0∘=mgsinθ×S−mg(HS)×S=mgH(∵sinθ=HS)
(4) Wfk=μN×S×cos180∘=−μmgcosθ×S=−μmg(LS)×S=−μmgL(∵cosθ=LS)
∴WTotal=mgH−μmgL
∴12mv2=mgH−μmgLorv=√2g(H−μL)

Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:IILUSTRATION
Explore 2 Videos
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTEChapter:WORK, ENERGY AND POWERExercise:TRY YOURSELF
Explore 95 Videos
- WAVESBook:AAKASH INSTITUTEChapter:WAVESExercise:ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
Explore 12 Videos
Similar Questions
The coefficient of friction between the block and the inclined plane is μ.
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View Solution
Knowledge Check
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θA block is released from rest from point on a rough inclined place of inclination 37∘. The coefficient of friction is 0.5.
AThe time taken to slide down 9 m on the plane is 3 s.BThe velocity of block after moving 4 m is m/s.CThe block travels equal distances in equal intervals of time.DThe velocity of block increases linearly.A block of mass 10 kg is released from top of rough inclined plane as shown in the figure if coefficient of friction between the block and inclined plane is then total work done on the block by all the forces acting on it till it reaches the bottom s = 10 ms
A200 jB300 jC100 jD-200 j
A block of mass 1kg is released from rest from the top of an inclined plane of inclination 45∘ .The coefficient of friction between block and the inclined plane varies with distance x from top position as μ=14(1+x) where x is in meter. Then block will have maximum speed after travelling a distance of ?
View SolutionIn the arrangement shown in figure coefficient of friction between 5kg block and incline plane is μ=0.5. Friction force acting on the 5kg block is

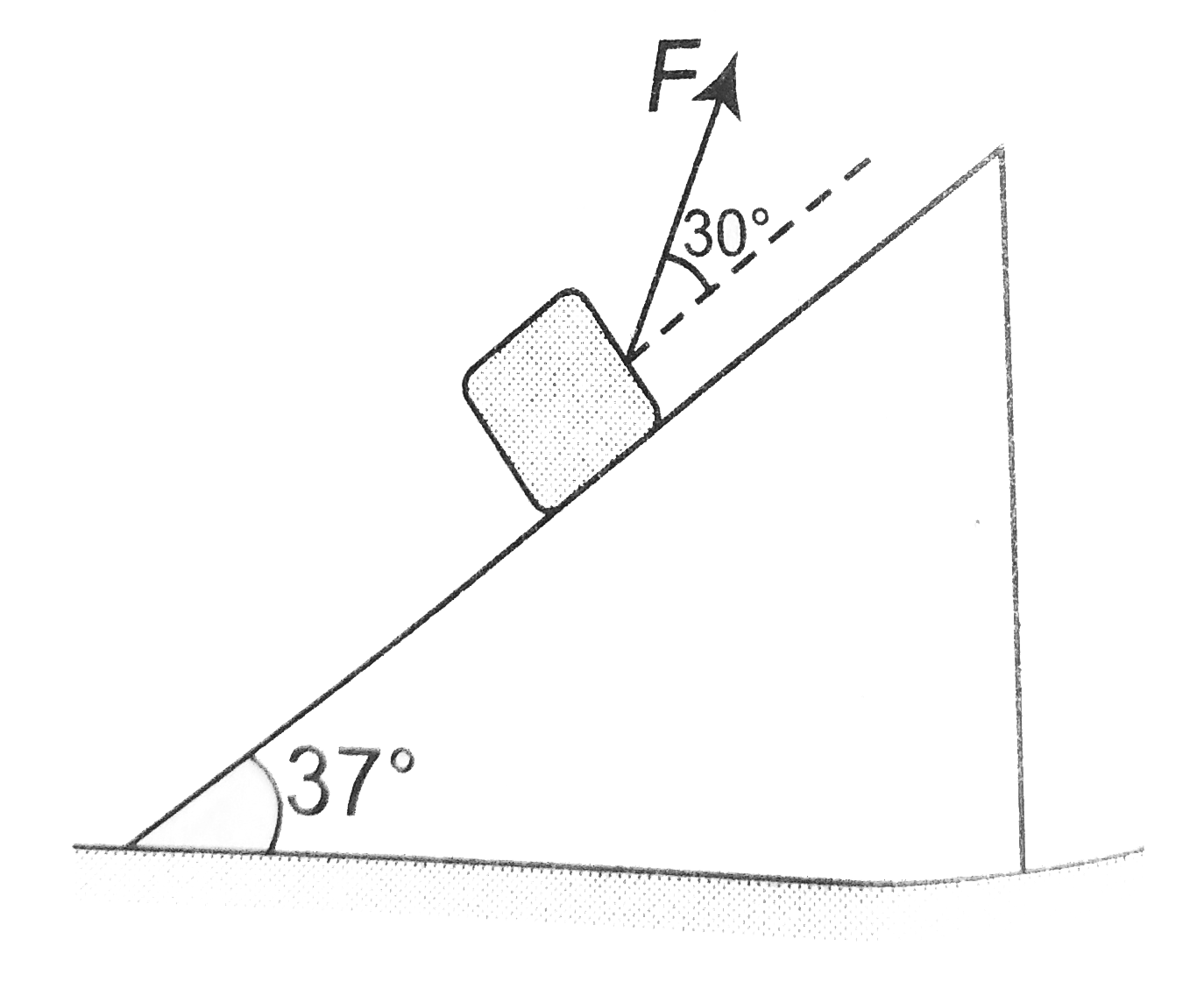
View SolutionA block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View Solution

