A block of mass m is slowly pulled along a curved surface from position 1 and 2. If the coefficient of kinetic friction between the block and surface is μ, find the work done by the applied force.
A block of mass m is slowly pulled along a curved surface from position 1 and 2. If the coefficient of kinetic friction between the block and surface is mu, find the work done by the applied force.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The forces acting on the block are gravity,
mg↓, N↑, fk↓, and F↑.
Using W-E theorem: W=ΔK
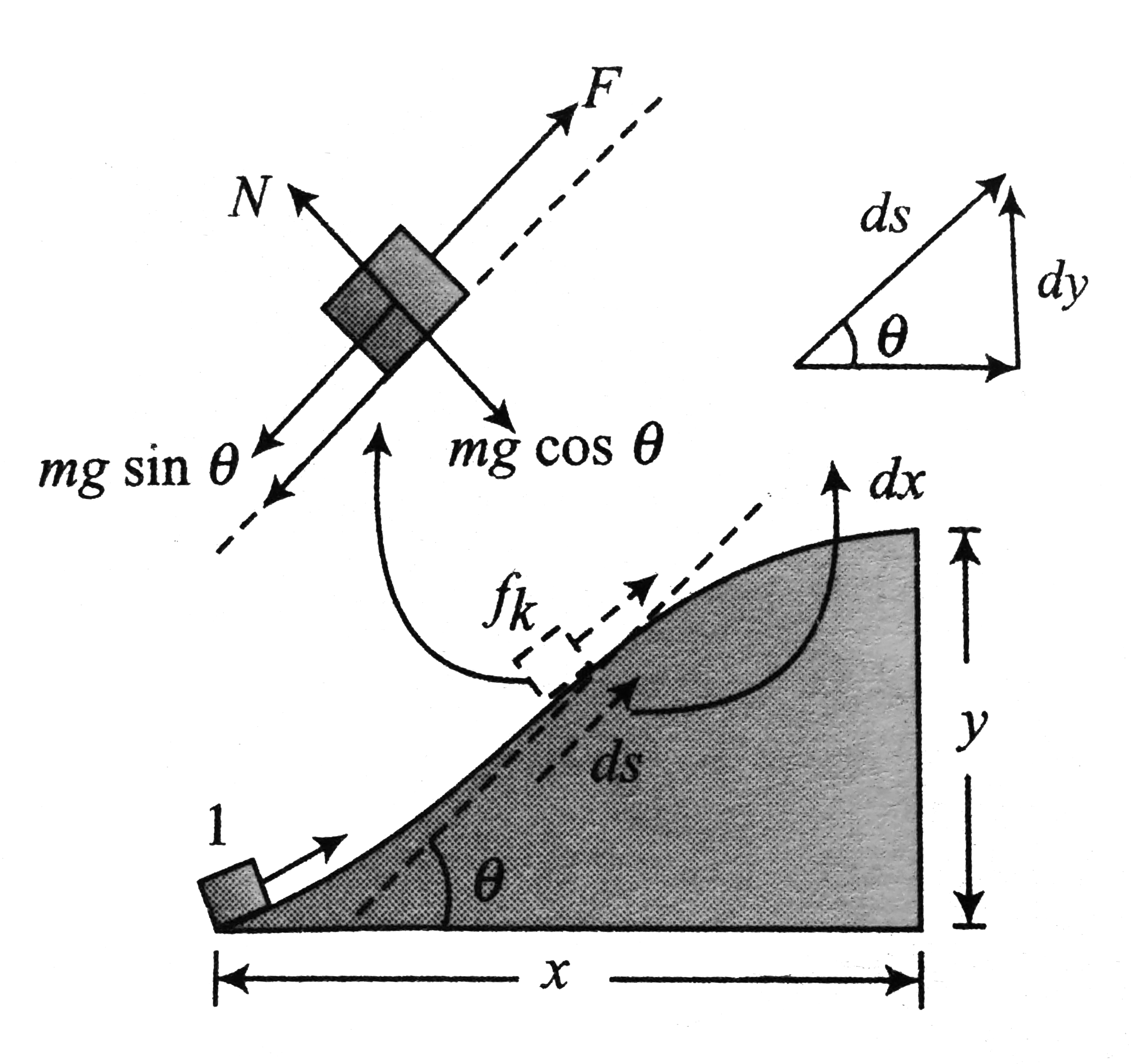
ocr_image
WN+Wgr+WN=Wf=ΔK (i)
For slowly shifting the body,
ΔK=0 (ii)
Work done normal reaction
WN=→N⋅d→s=0 (∴N⊥ds) (iii)
Work done by the gravity
Wgr=−mgy ( ∴ the block moves up) (iv)
Using equations(i), (ii), (iii), and (iv),
WF+Wf=mgy (v)
Wf=∫→fk⋅→ds
=∫fkdscos180∘
=−∫fkds=−∫μNds
=−∫μ(mgcosθ)ds
=−μmg∫dscosθ(dscosθ)=dx)
=−μmg∫x0dx=−μmgx (vi)
Using equations (v) and (vi), WF=mg(μx+y)

Updated on:21/07/2023
|
Class 11PHYSICSWORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • A block of mass M is using on a rough horizontal surface. μR is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?

    AMg
    BμMg
    CMg√1+μ2K
    DMg√1−μ2K

  • A block of mass m is stationary on a horizontal surface. It is connected with a string which has no tension. The coefficient of friction between the block and surface is m . Then , the frictional force between the block and surface is:
    ocr_image

    Azero
    Bμmg
    Cμmgμ
    DNone of these

  • A block of mass m is slowly carried on a inclined plane by a force F which always acts along the tangent to the plane. If the co-efficient of friction between the block and incline be μ, then work done by force of friction while carrying block from bottom of the plane to the top will be :
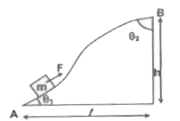    ocr_image

    Adependent on the actual shape of the path between point A and B.
    Bwill have a total positive value
    Cwill not change if force F is not applied along the tangent to the plane always.
    Dindependent of the actual shape of the path between points A and B.