A block is placed over a plank. The coefficient of friction between the block and the plank is μ=0.2. Initially both are at rest, suddenly the plank starts moving with acceleration a0=4m/s2. The displacement of the block in 1 is (g=10m/s2)
1 m relative to ground
1 m relative to plank
zero relative to plank
2 m relative to ground
The correct Answer is:A, B
To solve the problem, we need to analyze the motion of the block placed on the plank when the plank starts moving with a certain acceleration. Here's a step-by-step breakdown of the solution:
Step 1: Understand the Forces Acting on the Block
The block is subjected to two main forces:
1. The gravitational force acting downward, which is mg.
2. The frictional force acting between the block and the plank, which can be calculated using the formula:
ffriction=μmg
where μ=0.2 and g=10m/s2.
Step 2: Calculate the Maximum Static Friction
Using the values provided:
ffriction=0.2×m×10=2m
Step 3: Analyze the Motion of the Plank
The plank accelerates to the right with an acceleration a0=4m/s2. The block will tend to remain at rest due to inertia, but the frictional force will act to accelerate it.
Step 4: Determine the Acceleration of the Block
The net force acting on the block can be expressed as:
fnet=ffriction−m⋅a
Where a is the acceleration of the block relative to the ground. The maximum frictional force is 2m, and the force due to the plank's acceleration is 4m.
Setting up the equation:
4m−2m=ma
This simplifies to:
2m=ma
Thus, the acceleration a of the block relative to the ground is:
a=2m/s2
Step 5: Calculate the Displacement of the Block
Using the equation of motion for displacement:
s=ut+12at2
where:
- u=0 (initial velocity),
- a=2m/s2,
- t=1s.
Substituting the values:
s=0⋅1+12⋅2⋅(1)2=1m
Step 6: Conclusion
The displacement of the block in 1 second, relative to the plank, is:
Displacement=1m
Final Answer
The correct option is that the displacement of the block is 1 meter relative to the plank.
---
The block is subjected to two main forces:
1. The gravitational force acting downward, which is mg.
2. The frictional force acting between the block and the plank, which can be calculated using the formula:
ffriction=μmg
where μ=0.2 and g=10m/s2.
Using the values provided:
ffriction=0.2×m×10=2m
The plank accelerates to the right with an acceleration a0=4m/s2. The block will tend to remain at rest due to inertia, but the frictional force will act to accelerate it.
The net force acting on the block can be expressed as:
fnet=ffriction−m⋅a
Where a is the acceleration of the block relative to the ground. The maximum frictional force is 2m, and the force due to the plank's acceleration is 4m.
4m−2m=ma
This simplifies to:
2m=ma
Thus, the acceleration a of the block relative to the ground is:
a=2m/s2
Using the equation of motion for displacement:
s=ut+12at2
where:
- u=0 (initial velocity),
- a=2m/s2,
- t=1s.
s=0⋅1+12⋅2⋅(1)2=1m
The displacement of the block in 1 second, relative to the plank, is:
Displacement=1m
The correct option is that the displacement of the block is 1 meter relative to the plank.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JM)
6 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (O-1)
51 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
Similar Questions
A block of mass 2kg is placed on a truck as shown in the figure. The coefficient of friction between the block and surface is 0.5. The truck starts from the rest and moves with acceleration a0. (a) Find the friction force acting on the block if (i) a0=2m/s2 , (ii) 4m/s2 , (iii) 6m/s2 and (b) if acceleration of truck a0=8m/s2. After how much time the blocks falls off the truck and the distance travelled by the truck in this time.

View Solution.A block is kept on the floor of an elevator at rest.The elevator starts descending with an acceleration of 12m/s^(2) .Find the displacement of the block during the first 0*2safter the start.Take g=10m/s^(2)
View Solution
Knowledge Check
A block is over a plank . The coefficient of friction between the block and the plank id μ=0.2Initially both are at rest , suddenly the plank starts moving with accleration α0=4m/s2 The displacement of the block in s is (g=10m/s2)
A1m relative to groundB1 m relative to plankCzero relative to plankD2 m relative to groundA block of mass 2 kg rests on a rough horizontal plank , the coefficient of friction between the plank and block is 0.3. If the plank is pulled horizontally with a constant acceleration of 4m/s2 , the distance moved by the block on the plank in 5 second starting from rest (in m) is : (Take g = 10m/s2)
A5B10C25D50A block of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
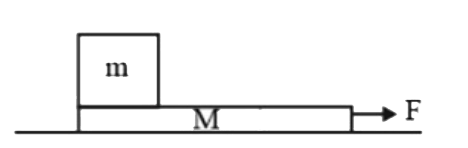 A50 NB40 NC120 ND100 N
A50 NB40 NC120 ND100 N
A block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between block and plank is 1/2. Plank is undergoing SHM is angular frequency 10rad/s. Find the maximum amplitude of plank in which the block does slip over plank (g=10m/s2).
View SolutionA block of mass m kg is placed on a plank. The plank is moving with an acceleration 6ˆi+6ˆj (in m/s2 ). The frictional force acting on the block is (μ=0.5,g=10m/s2) :
View SolutionA block of mass 4kg is placed in contact with the front vertical surface of a lorry.The coefficient of friction between the vertical surface and block is 0.8.The lorry is moving with an acceleration of 15m/s2.The force of friction between lorry and block is (g=10ms−2)
View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View Solution