A block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
4cm
5cm
10 cm
16 cm
The correct Answer is:B
To solve the problem step by step, we will analyze the forces acting on the block and the conditions under which it does not slip on the plank undergoing simple harmonic motion (SHM).
1. Identify the Forces:
- The block experiences a gravitational force mg acting downwards.
- The normal force N acts upwards, which is equal to mg since there is no vertical motion.
- The frictional force f that prevents the block from slipping is given by f=μN=μmg, where μ is the coefficient of friction.
2. Acceleration Due to SHM:
- The plank is undergoing SHM with angular frequency ω=10rad/s.
- The acceleration a of the plank at maximum displacement (amplitude x) is given by:
a=−ω2x
- The negative sign indicates that the acceleration is directed towards the mean position.
3. Condition for No Slipping:
- For the block to not slip, the maximum pseudo force (which is the inertial force due to the acceleration of the plank) must be less than or equal to the maximum frictional force:
fmax=μmg
- The pseudo force acting on the block due to the SHM of the plank is:
Fpseudo=ma=m(−ω2x)
4. Setting Up the Equation:
- For the block to remain at rest relative to the plank, we set the magnitudes of the forces equal:
μmg=mω2x
- We can cancel m from both sides (assuming m≠0):
μg=ω2x
5. Solving for Maximum Amplitude x:
- Rearranging the equation gives:
x=μgω2
6. Substituting Values:
- Given μ=12, g=10m/s2, and ω=10rad/s:
x=12⋅10102=5100=120m
7. Final Answer:
- Converting to centimeters:
x=120m=5cm
Conclusion:
The maximum amplitude of the plank in which the block does not slip over it is 5 cm.
- The block experiences a gravitational force mg acting downwards.
- The normal force N acts upwards, which is equal to mg since there is no vertical motion.
- The frictional force f that prevents the block from slipping is given by f=μN=μmg, where μ is the coefficient of friction.
- The plank is undergoing SHM with angular frequency ω=10rad/s.
- The acceleration a of the plank at maximum displacement (amplitude x) is given by:
a=−ω2x
- The negative sign indicates that the acceleration is directed towards the mean position.
- For the block to not slip, the maximum pseudo force (which is the inertial force due to the acceleration of the plank) must be less than or equal to the maximum frictional force:
fmax=μmg
- The pseudo force acting on the block due to the SHM of the plank is:
Fpseudo=ma=m(−ω2x)
- For the block to remain at rest relative to the plank, we set the magnitudes of the forces equal:
μmg=mω2x
- We can cancel m from both sides (assuming m≠0):
μg=ω2x
- Rearranging the equation gives:
x=μgω2
- Given μ=12, g=10m/s2, and ω=10rad/s:
x=12⋅10102=5100=120m
- Converting to centimeters:
x=120m=5cm
The maximum amplitude of the plank in which the block does not slip over it is 5 cm.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:More than one option is correct
Explore 50 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Comprehension types
Explore 18 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Only one question is correct
Explore 48 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEYChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
A block is kept on a rough horizontal plank. The coefficient of friction between block and plank is 1/2. Plank is undergoing SHM is angular frequency 10rad/s. Find the maximum amplitude of plank in which the block does slip over plank (g=10m/s2).
View SolutionA block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

View Solution
Knowledge Check
A block of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
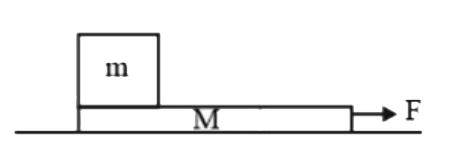 A50 NB40 NC120 ND100 N
A50 NB40 NC120 ND100 NA block of mass 2 kg rests on a rough horizontal plank , the coefficient of friction between the plank and block is 0.3. If the plank is pulled horizontally with a constant acceleration of 4m/s2 , the distance moved by the block on the plank in 5 second starting from rest (in m) is : (Take g = 10m/s2)
A5B10C25D50A small wooden cube is placed on a plank. The plank performs a vertical S.H.M. of frequency 3πHz. What is the maximum amplitude of its vertical S.H.M., so that the wooden cube does not leave the plank ?[g=10m/s2]
A512mB518mC712mD1118m
A block of mass M=4kg of height and breath b is placed on a rough plank of same mass M. A light inextensible string is connected to the upper end of the block and passed through a light smooth pulley as shown in figure. A mass m=1kg is hung to the other end of the string.
a. What should be the minimum value of coefficient of friction between the block and the plank so that, there is no slipping between the block and the wedge?
b. Find the minimum value of b/h so that the block does not topple over the plank, friction is absent between the plank and the ground.

View SolutionA block is over a plank . The coefficient of friction between the block and the plank id μ=0.2Initially both are at rest , suddenly the plank starts moving with accleration α0=4m/s2 The displacement of the block in s is (g=10m/s2)
View SolutionA block is placed over a plank. The coefficient of friction between the block and the plank is μ=0.2. Initially both are at rest, suddenly the plank starts moving with acceleration a0=4m/s2. The displacement of the block in 1 is (g=10m/s2)
View SolutionA block of mass m is gently placed over a massive plank moving horizontal over a smooth surface with velocity 10ms−1. The coefficient of friction between the block and the plank is 0.2. The distance travelled by the block till it slides on the plank is [g=10ms−2]
View SolutionA small block of mass 1kg is placed over a plank of mass 2kg. The length of the plank is 2 m. coefficient of friction between the block and the plnak is 0.5 and the ground over which plank in placed is smooth. A constant force F=30N is applied on the plank in horizontal direction. the time after which the block will separte from the plank is (g=10m/s2)
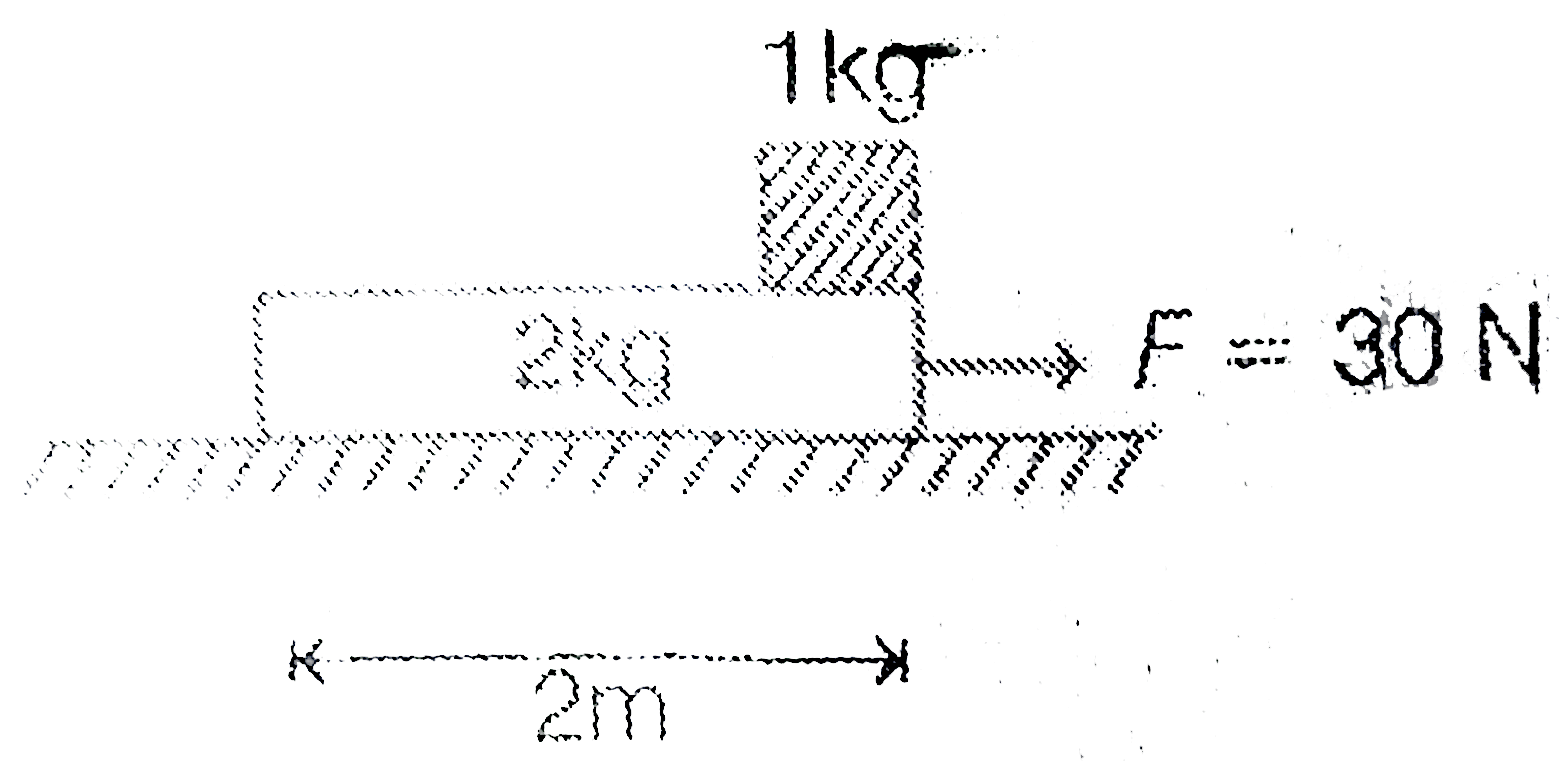
View Solution

