A block of mass m is gently placed over a massive plank moving horizontal over a smooth surface with velocity 10ms−1. The coefficient of friction between the block and the plank is 0.2. The distance travelled by the block till it slides on the plank is [g=10ms−2]
10 m
15m
25 m
35m
The correct Answer is:C
To solve the problem step by step, we can follow these steps:
Step 1: Understand the Problem
We have a block of mass m placed on a plank that is moving horizontally with a velocity of 10m/s. The coefficient of friction between the block and the plank is μ=0.2. We need to find the distance traveled by the block until it starts sliding on the plank.
Step 2: Analyze the Forces
When the block is placed on the moving plank, it initially has a velocity of 0m/s relative to the plank. The frictional force acting on the block is what allows it to accelerate and catch up to the velocity of the plank.
The frictional force Ff can be given by:
Ff=μmg
where g=10m/s2 (acceleration due to gravity).
Step 3: Calculate the Acceleration
The acceleration a of the block due to the frictional force is:
a=Ffm=μmgm=μg
Substituting the values:
a=0.2×10=2m/s2
Step 4: Use Kinematic Equations
We can use the kinematic equation to find the distance s traveled by the block until it reaches the velocity of the plank:
v2=u2+2as
Where:
- v=10m/s (final velocity of the block when it matches the plank's speed)
- u=0m/s (initial velocity of the block)
- a=2m/s2 (acceleration)
Substituting the values into the equation:
(10)2=(0)2+2×2×s
100=4s
s=1004=25m
Step 5: Conclusion
The distance traveled by the block until it starts sliding on the plank is 25m.
We have a block of mass m placed on a plank that is moving horizontally with a velocity of 10m/s. The coefficient of friction between the block and the plank is μ=0.2. We need to find the distance traveled by the block until it starts sliding on the plank.
When the block is placed on the moving plank, it initially has a velocity of 0m/s relative to the plank. The frictional force acting on the block is what allows it to accelerate and catch up to the velocity of the plank.
Ff=μmg
where g=10m/s2 (acceleration due to gravity).
The acceleration a of the block due to the frictional force is:
a=Ffm=μmgm=μg
Substituting the values:
a=0.2×10=2m/s2
We can use the kinematic equation to find the distance s traveled by the block until it reaches the velocity of the plank:
v2=u2+2as
Where:
- v=10m/s (final velocity of the block when it matches the plank's speed)
- u=0m/s (initial velocity of the block)
- a=2m/s2 (acceleration)
(10)2=(0)2+2×2×s
100=4s
s=1004=25m
The distance traveled by the block until it starts sliding on the plank is 25m.
Topper's Solved these Questions
Similar Questions
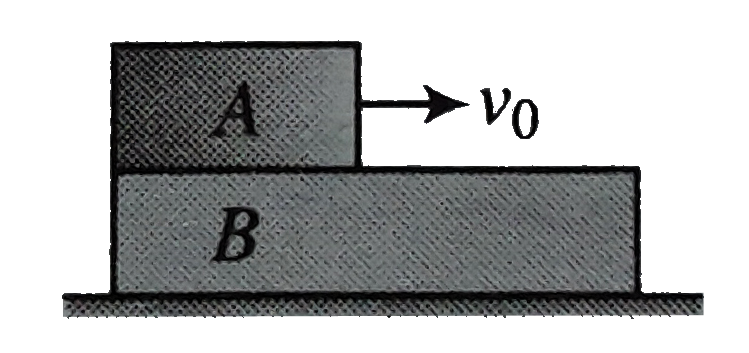
A block A of mass m is placed over a plankB of mass 2m plank B is placed over a smooth horizontal surface .The coefficient of friction between A and B is 0.4 Block A is given a velocity v0 toward right Find acceleration (in ms−2 of B relative to A
View SolutionA block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

View Solution
Knowledge Check
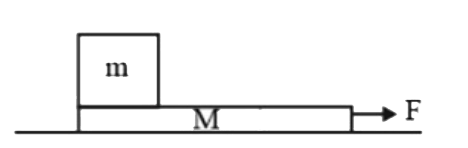
A block of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
 A50 NB40 NC120 ND100 N
A50 NB40 NC120 ND100 NA block of mass 2kg is placed on the surface of trolley of mass 20kg which is on a smooth surface.The coefficient of friction between the block and the surface of the trolley is 0.25.If a horizontal force of 2N acts on the block, the acceleration of the system in ms−2 is (g=10ms−2)
A1.8B1.0C0.9D0.09A block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
A4cmB5cmC10 cmD16 cm
A plank of mass M and length L is placed at rest on a smooth horizontal surface A small block of mass m is projected wii:h a velocity v0 as shown in the Fig. 3.31 (a), The coefficient of friction between the block and the plank is μ, plank is very long so that block eventually comes to rest on it.
(i) Find the work done by the ftjctioh force on the block during the period it slides on the plank. Is the Work positive or negative ?'
(ii) Calculate the work done on the plank during the same period. Is the work positive or negative?
(iii) Also, determine the net work done by friction. Is it positive or negative ?

View SolutionA block of mass 0.5 kg has an initial velocity of 10ms−1 down an inclined plane of angle 30∘, the coefficient of friction between the block and the inclined surface is 0.2. The velocity of the block after it travels a distance of 10 m is

View SolutionA block A of mass m is placed over a plank B of mass 2m. Plank B is placed over a smooth horizontal surface. The coefficient of friction between A and B is 12 block A is given a velocity v0 towards right. Accelration of B relative to A is

View SolutionA small block of mass 1kg is placed over a plank of mass 2kg. The length of the plank is 2 m. coefficient of friction between the block and the plnak is 0.5 and the ground over which plank in placed is smooth. A constant force F=30N is applied on the plank in horizontal direction. the time after which the block will separte from the plank is (g=10m/s2)
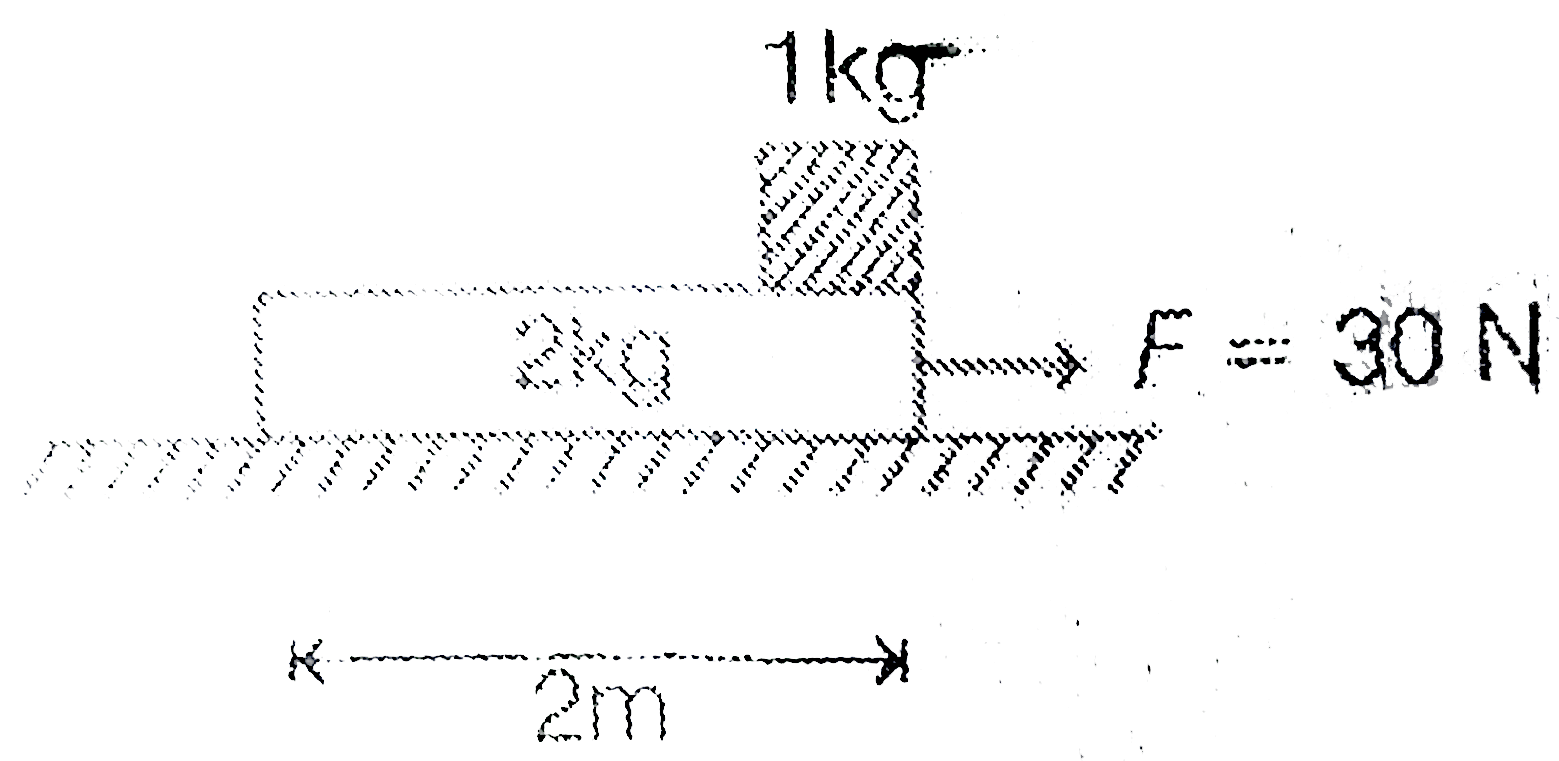
View SolutionA block of mass m=2kg is placed in equilibrium on a moving plank accelerating with a=1m/s2 . If coefficient of friction between plank and block μ=0.2 . The friction force acting on theblock is:
View Solution

