A small block of mass 1kg is placed over a plank of mass 2kg. The length of the plank is 2 m. coefficient of friction between the block and the plnak is 0.5 and the ground over which plank in placed is smooth. A constant force F=30N is applied on the plank in horizontal direction. the time after which the block will separte from the plank is (g=10m/s2)
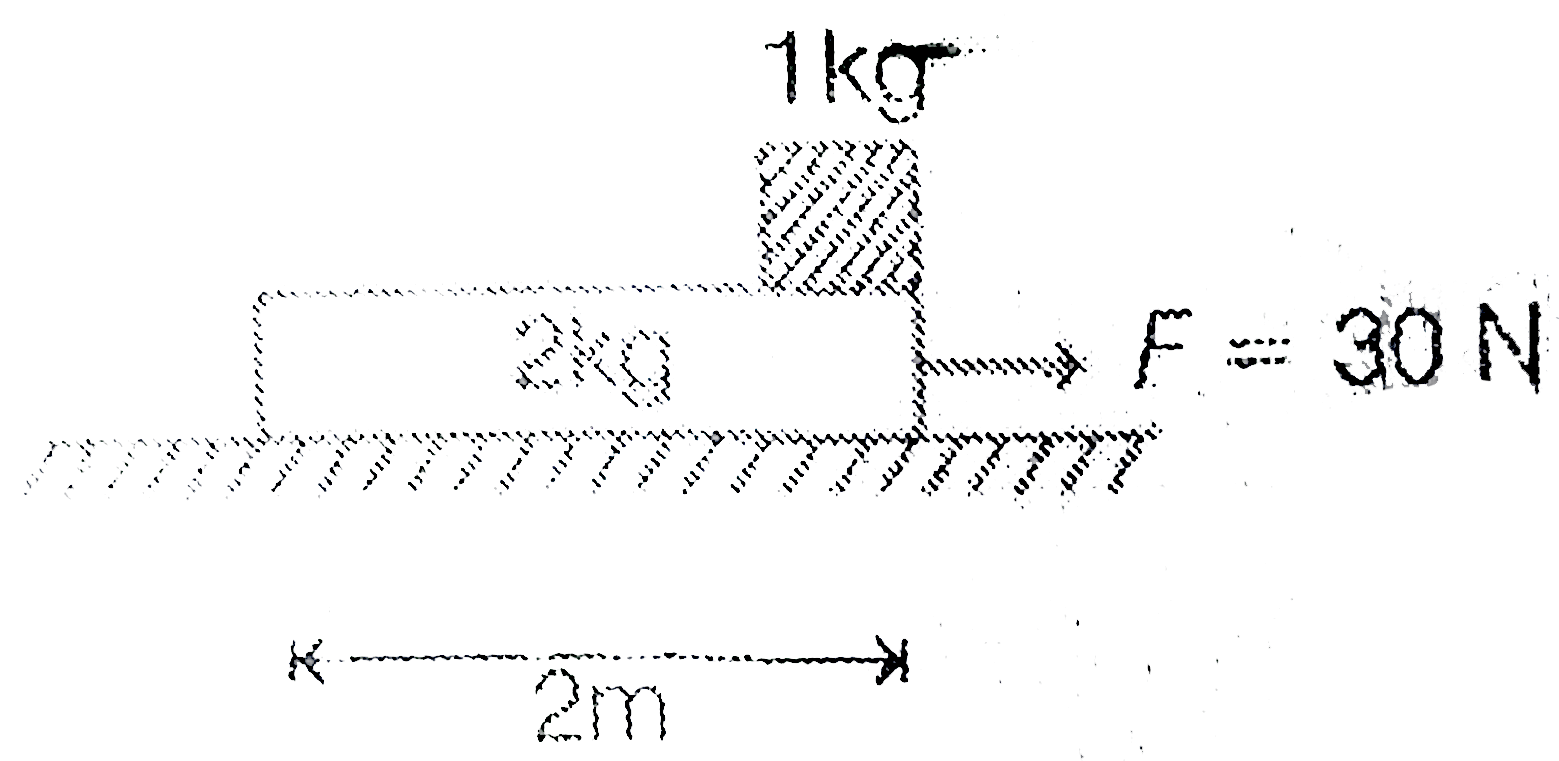
0.89s
1.2s
0.62s
1.6s
The correct Answer is:a
Step by step video, text & image solution for A small block of mass 1kg is placed over a plank of mass 2kg. The length of the plank is 2 m. coefficient of friction between the block and the plnak is 0.5 and the ground over which plank in placed is smooth. A constant force F=30N is applied on the plank in horizontal direction. the time after which the block will separte from the plank is (g=10m//s^(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

View SolutionA block of mass'm' it kept over the smooth surface of the plank of mass M. the plank of length l is kept over the smooth horizontal surface. A constant horizontal force F is applied onto the plank as shown in figure. Calculate the time after which the block falls off the plank?

View Solution
Knowledge Check
A plank of mass 2kg and length 1m is placed on horizontal floor.A small block of mass 1kg is placed on top of the plank , at its right extreme end .The coefficient of friction between plank and floor is 0.5 and that between plank and block is 0.2 . If a horizontal force =30N starts acting on the plank to the right ,the time after which the block will fall off the plank is (g=10ms−2)
A(23)sB1.5sC0.75sD(43)sA block of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
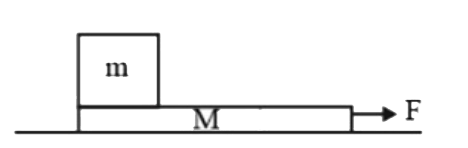 A50 NB40 NC120 ND100 N
A50 NB40 NC120 ND100 NA block of mass m=2kg is placed in equilibrium on a moving plank accelerating with a=1m/s2 . If coefficient of friction between plank and block μ=0.2 . The friction force acting on theblock is:
A2NB4NC3NDNone of these
A plank of mass 10kg rests on a smooth horizontal surface. Two blocks A and B of masses mA=2kgandmB=1kg lies at a distance of 3m on the plank as shown in the distance of 3m on the plank as shown in the figure. The friction coefficient between the blocks and plank are μA=0.3andμB=0.1. Now a force F = 15 N is applied to the plank in horizontal direction. Find the time after which block A collides with B.
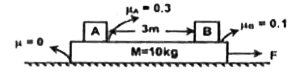
View SolutionA block of mass m=2kg is placed in equilibrium on a moving plank accelerating with a=4m/s2 . If coefficient of friction between plank and block μ=0.2 . The friction force acting on the block is:
View SolutionA plank of mass 10 kg and a block of mass 2 kg are placed on a horizontal plane as shown in the figure. There is no friction between plane and plank. The coefficient of friction between block and plank is 0.5 .A force of 60 N is applied on plank horizontally. In first 2 s the work done by friction on the block is

View SolutionA block of mass m is gently placed over a massive plank moving horizontal over a smooth surface with velocity 10ms−1. The coefficient of friction between the block and the plank is 0.2. The distance travelled by the block till it slides on the plank is [g=10ms−2]
View SolutionA bar of mass m1 is placed on a plank of mass m2 which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t0 at which the plank starts sliding is :

View Solution

