A mass M is performing linear simple harmonic motion. Then correct graph for acceleration a and corresponding linear velocity v is

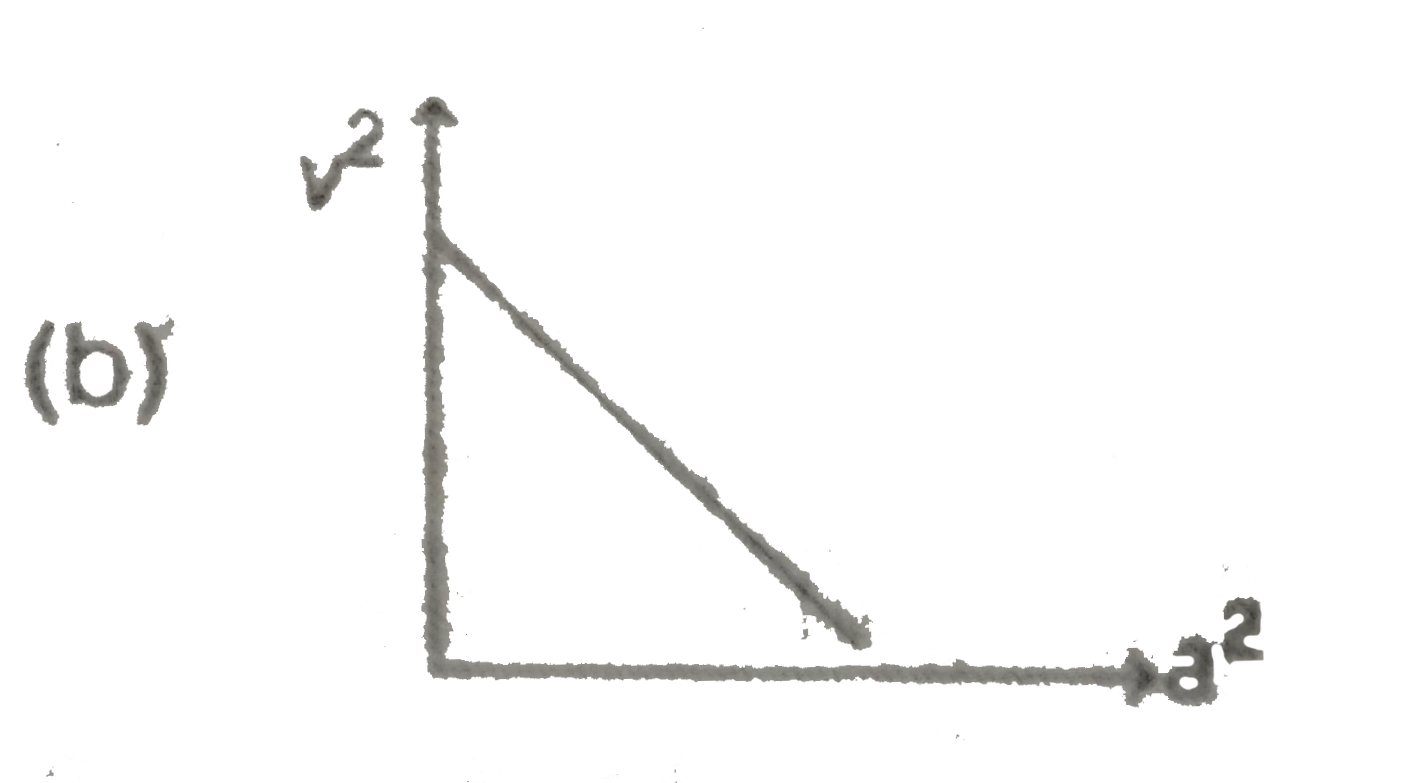


The correct Answer is:B
To solve the problem of determining the correct graph for the relationship between acceleration a and linear velocity v for a mass M performing linear simple harmonic motion, we can follow these steps:
1. Define the Displacement Equation:
The displacement x of a mass in simple harmonic motion can be expressed as:
x=Asin(ωt)
where A is the amplitude and ω is the angular frequency.
Hint: Remember that the sine function oscillates between -1 and 1, which is crucial for understanding the motion.
2. Calculate the Velocity:
To find the velocity v, we differentiate the displacement with respect to time t:
v=dxdt=Aωcos(ωt)
Hint: The velocity is maximum when cos(ωt) is at its maximum value (1).
3. Calculate the Acceleration:
The acceleration a is the derivative of velocity with respect to time:
a=dvdt=−Aω2sin(ωt)
Hint: Notice that acceleration is directly related to the sine function, which indicates its oscillatory nature.
4. Relate v and a:
From the equations for v and a, we can express cos(ωt) and sin(ωt):
cos(ωt)=vAω
sin(ωt)=−aAω2
5. Square Both Equations:
Squaring both equations gives:
cos2(ωt)=v2A2ω2
sin2(ωt)=a2A2ω4
6. Use the Pythagorean Identity:
Using the identity sin2(θ)+cos2(θ)=1:
v2A2ω2+a2A2ω4=1
7. Rearranging the Equation:
Rearranging gives:
v2=A2ω2−a2ω2
This shows a linear relationship between v2 and a2.
8. Identify the Graph:
The equation v2=A2ω2−a2ω2 indicates that as a increases, v2 decreases, which corresponds to a straight line with a negative slope. The x-intercept is positive.
Hint: Look for a graph that shows a linear relationship with a negative slope.
9. Conclusion:
Based on the analysis, the correct graph that represents the relationship between acceleration a and linear velocity v is option D.
The displacement x of a mass in simple harmonic motion can be expressed as:
x=Asin(ωt)
where A is the amplitude and ω is the angular frequency.
To find the velocity v, we differentiate the displacement with respect to time t:
v=dxdt=Aωcos(ωt)
The acceleration a is the derivative of velocity with respect to time:
a=dvdt=−Aω2sin(ωt)
From the equations for v and a, we can express cos(ωt) and sin(ωt):
cos(ωt)=vAω
sin(ωt)=−aAω2
Squaring both equations gives:
cos2(ωt)=v2A2ω2
sin2(ωt)=a2A2ω4
Using the identity sin2(θ)+cos2(θ)=1:
v2A2ω2+a2A2ω4=1
Rearranging gives:
v2=A2ω2−a2ω2
This shows a linear relationship between v2 and a2.
The equation v2=A2ω2−a2ω2 indicates that as a increases, v2 decreases, which corresponds to a straight line with a negative slope. The x-intercept is positive.
Based on the analysis, the correct graph that represents the relationship between acceleration a and linear velocity v is option D.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:More than one option is correct
Explore 50 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Comprehension types
Explore 18 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Only one question is correct
Explore 48 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEYChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
Velocity of a body moving in simple harmonic motion is
View SolutionState of differential equation equation of linear simple harmonic motion. Hence obtain the expression for acceleration, velocity and displacement of a particle performing linear S.H.M.
A body cools from 80∘C to 70∘C in 5 minutes and to 62∘C in the next 5 minutes. Calculate the temperature of the surroundings.
View Solution
Knowledge Check
A body is performing simple harmonic motion. Then its
Aaverage total energy per cycle is equal to its maximum kinetic energy.Baverage kinetic energy per cycle is equal to half of its maximum kinetic energy.Caverage total energy per cycle is equal to half of its malximum kinetic energy.DNone of these.A particle is performing a linear simple harmonic motion if the acceleration and the corresponding velocity of the particle are a and v respectively. Which of the following graph is correct?
A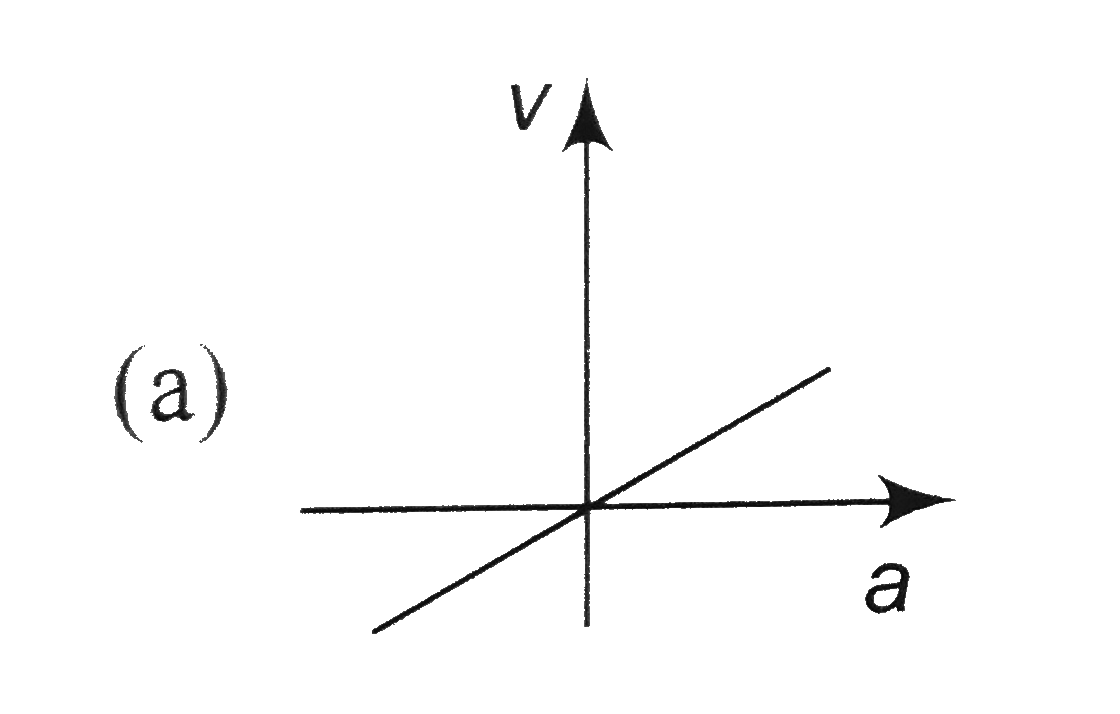 B
B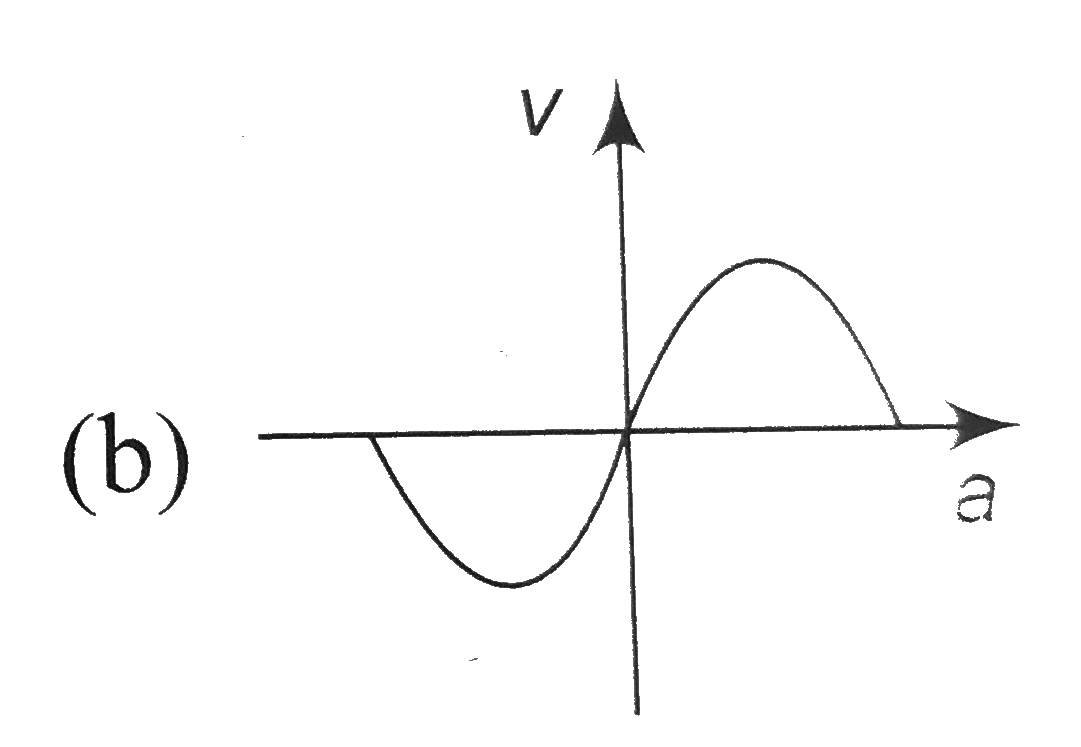 C
C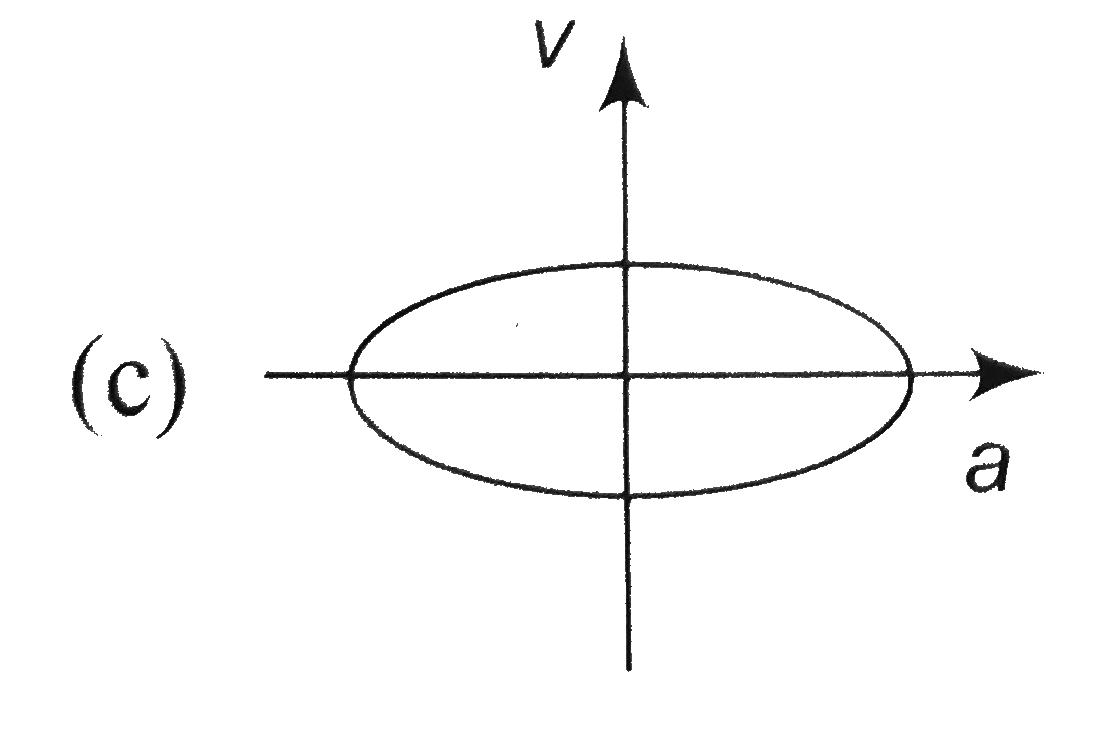 D
D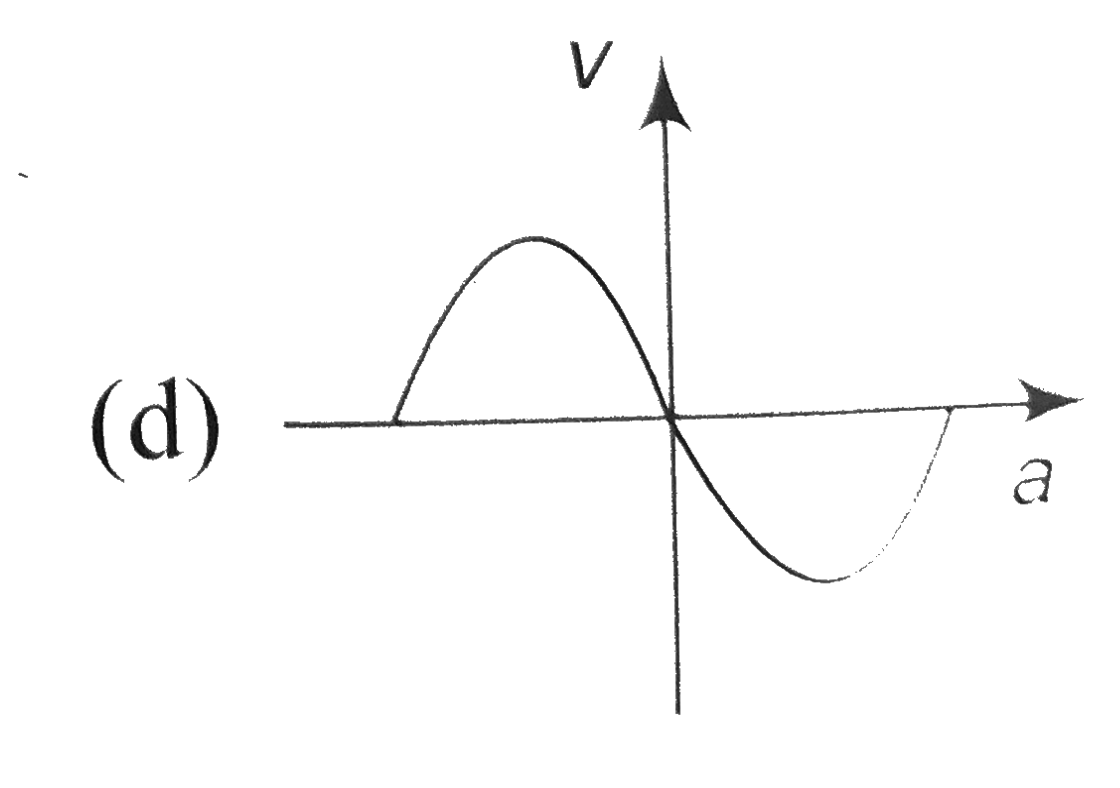
A particle is performing a linear simple harmonic motion. If the instantaneous acceleration and velocity of the particle are a and v respectively, identify the graph which correctly represents the relation between a and v.
A B
B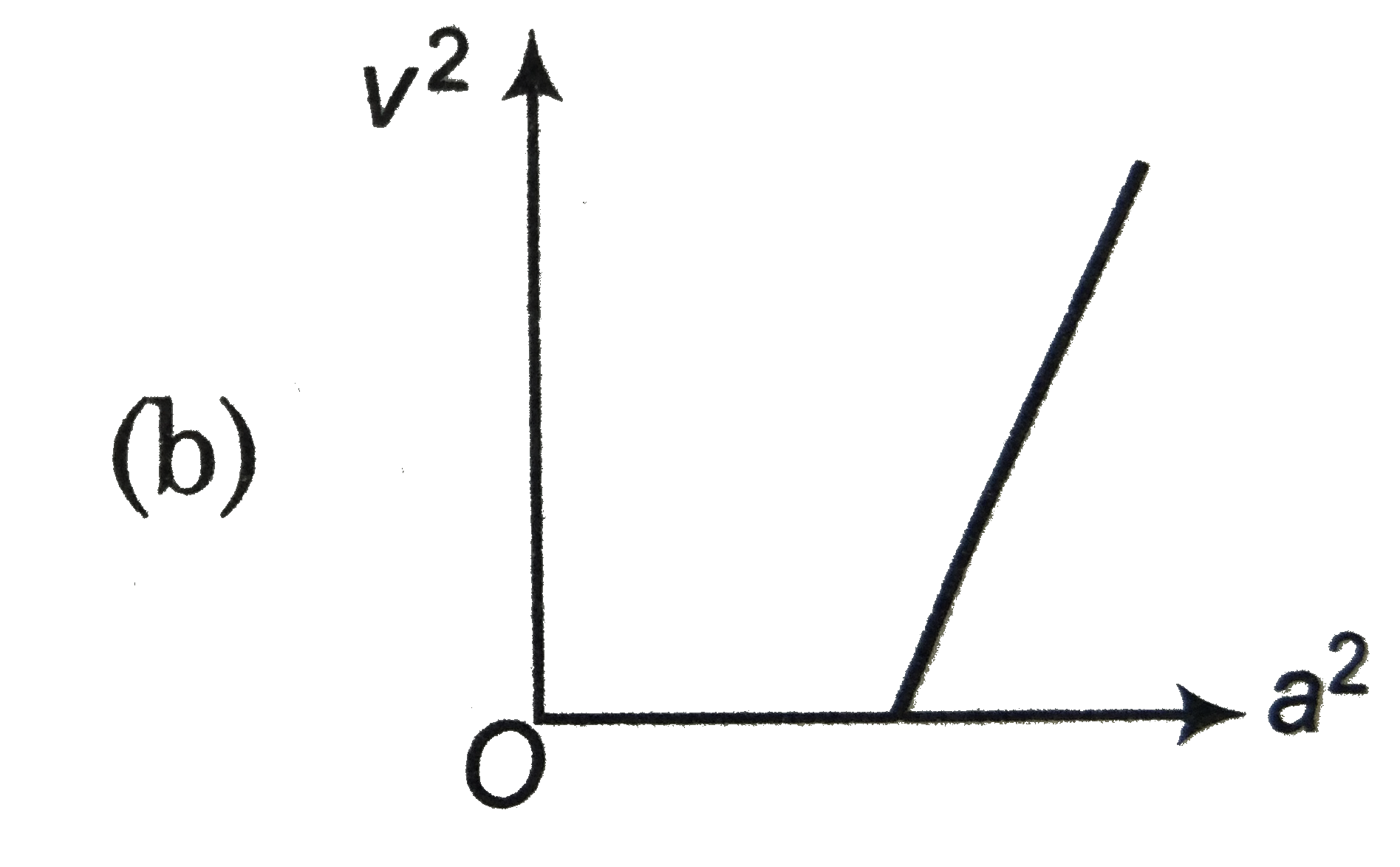 C
C D
D
For a particle executing simple harmonic motion, the acceleration is proportional to
View SolutionA mass m is performing linear simple harmonic motion, then which of the following graph represents correctly the variation of acceleration a corresponding to linear velocity υ ?
View SolutionWhile a particle executes linear simple harmonic motion
View SolutionIf a particle is executing simple harmonic motion, then acceleration of particle
View SolutionA body of mass 40g is executing linear simple harmonic motion and has a velocity of 2cm/s when its displacement is 3cm and a velocity of 3 cm/s when its displacement is 2cm . Then
View Solution

