A test tube of length l and area of cross-section A has some iron fillings of mass M. The test tube floats normally in a liquid of density ρ with length x dipped in the liquid. A distribuing force makes the tube oscillate in the liquid. The time period of osciallation is given by (neglect the mass of the test tube)
(2π√MρAg
2π√xg
2π√lg
2π√Mg
The correct Answer is:B
Step by step video, text & image solution for A test tube of length l and area of cross-section A has some iron fillings of mass M. The test tube floats normally in a liquid of density rho with length x dipped in the liquid. A distribuing force makes the tube oscillate in the liquid. The time period of osciallation is given by (neglect the mass of the test tube) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:More than one option is correct
Explore 50 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Comprehension types
Explore 18 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Only one question is correct
Explore 48 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEYChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
A glass tube is floating in a liquid with 30 cm of its length immersed in the liquid. If the glass tube is pushed down and released, then calculate the time period of vibration of glass tube.
View SolutionA test tube of uniform cross-section is floated vertically in a liquid 'A' (density ρA) upto a mark on it when it is filled with 'x' ml of a liquid 'B' (density ρB). To make the test tube float in liquid B upto the same mark it is filled with y ml of the liquid A. Find the mass of the test tube.
View Solution
Knowledge Check
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
AT∝√ρBT∝1√ACT∝1√ρDT∝1√mWhen a loaded test tube floats vertically with 13 and 14 of the lengths inside two liquids, then the ratio of the densities of the two liquids is
A3:4B4:3C9:16D16:2A U tube pf uniform born of cross sectional area A has been set up vertically with open ends facing up Now mgm of a liquid of density d is poured into it. The column of liquid in this tube will oscillation with a period T such that
AT=2π√MgBT=2π√MAgdCT=2π√MgdADT=2π√M2Adg
Find time period of liquid column of length l in the shown tube.

View SolutionA plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
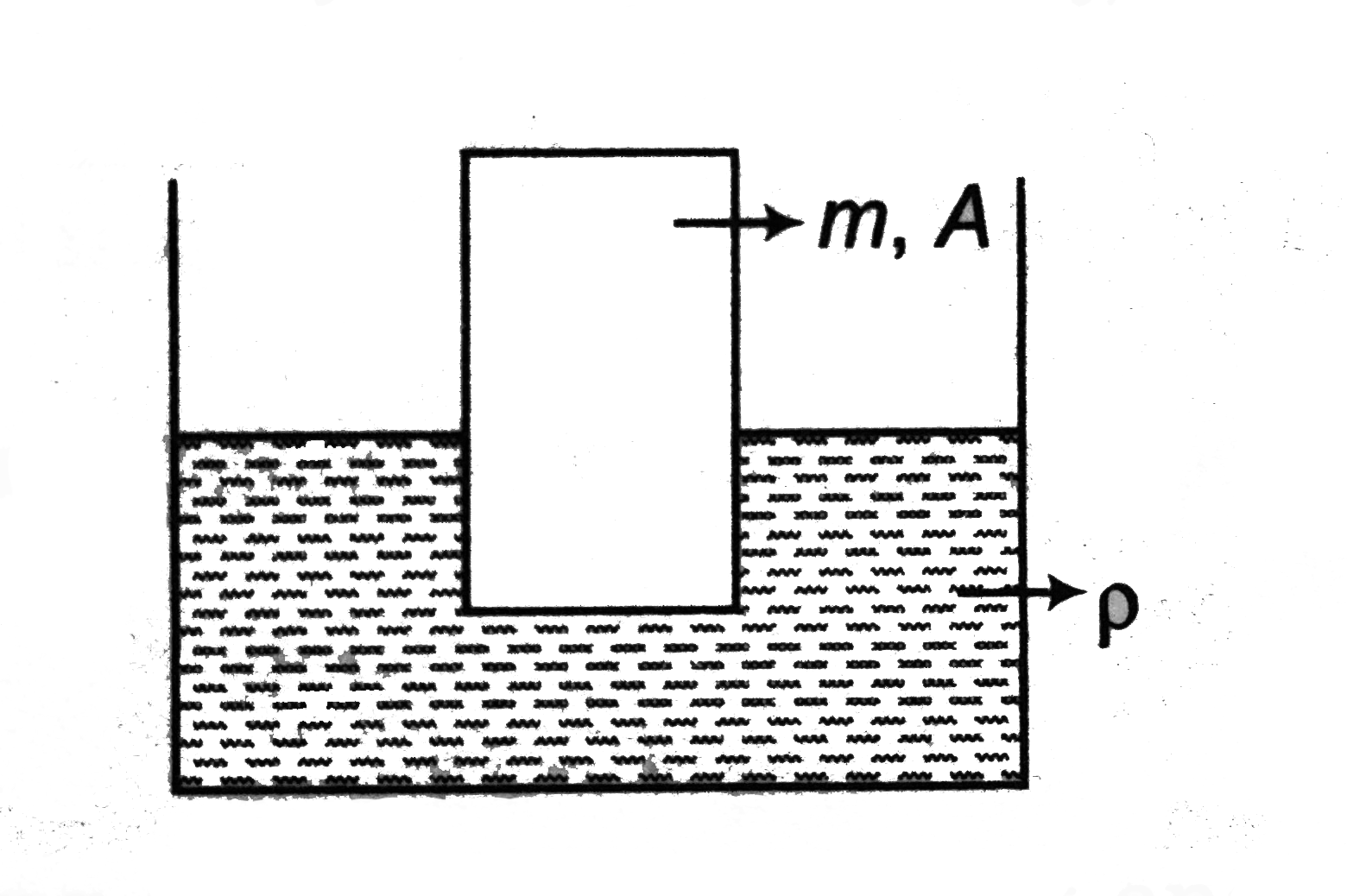
View SolutionA test tube of uniform cross-section is floated vertically in a liquid 'A' (density ρA) upto a mark on it when it is filled with 'x' ml of a liquid 'B' (density ρB). To make the test tube float in liquid B upto the same mark it is filled with y ml of the liquid A. Find the mass of the test tube.
View SolutionWhen a capillary tube of radius r is immersed in a liquid of density ρ, the liquid rises to a height h in it. If m is the mass of the liquid in the capillary tube, find the potential energy of this mass of the liquid in the tube.
View SolutionA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
View Solution
